Loading... 首先看看一道题 ## 区间和 假定有一个无限长的数轴,数轴上每个坐标上的数都是 0。 现在,我们首先进行 n 次操作,每次操作将某一位置 x 上的数加 c。 接下来,进行 m 次询问,每个询问包含两个整数 l 和 r,你需要求出在区间 [l,r] 之间的所有数的和。 #### 输入格式 第一行包含两个整数 n 和 m。 接下来 n 行,每行包含两个整数 x 和 c。 再接下来 m 行,每行包含两个整数 l 和 r。 #### 输出格式 共 m 行,每行输出一个询问中所求的区间内数字和。 #### 数据范围 −109≤x≤109 1≤n,m≤105 −109≤l≤r≤109 −10000≤c≤10000 #### 输入样例: ``` 3 3 1 2 3 6 7 5 1 3 4 6 7 8 ``` #### 输出样例: ``` 8 0 5 ``` #### 参考程序 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 300010; int n, m; int a[N], s[N]; vector<int> alls; vector<pair<int,int>> add, query; int find(int x) { int l = 0, r = alls.size() - 1; while(l < r) { int mid = l + r >> 1; if (alls[mid] >= x) r = mid; else l = mid + 1; } return r + 1; } int main() { cin >> n >> m; for (int i = 0; i < n; i++) { int x, c; cin >> x >> c; add.push_back({x, c}); alls.push_back(x); } for (int i = 0; i < m; i++) { int l, r; cin >> l >> r; query.push_back({l, r}); alls.push_back(l); alls.push_back(r); } // 排序去重 sort(alls.begin(), alls.end()); alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 处理插入 for (auto item: add) { int x = find(item.first); a[x] += item.second; } // 预处理前缀和 for (int i = 1; i <= alls.size(); i++) s[i] = s[i - 1] + a[i]; // 处理询问 for (auto item:query) { int l = find(item.first), r = find(item.second); cout << s[r] - s[l - 1] << endl; } return 0; } ``` ## 题目描述 首先明确一下题意,先输入两个整数`n`、`m`,`n`代表在区间`[-1e9,1e9]`某一点加一个整数的次数,输入`x` `c`在`x`处加上`c`,`m`代表求某个区间和的次数,输入`l` `r`求区间`[l,r]`的和。 ## 分析 分析一下代码。 主要分为5大步: 1.读输入。将每次读入的`x` `c` `push_back()`到`add`中,将每次读入的位置`x` `push_back()`到`alls`中,将每次读入的`l` `r` `push_back()`到`query`中。 2.排序、去重。 3.通过遍历`add`,完成在离散化的数组映射到的`a`数组中进行加上`c`的操作(用到`find`函数)。 4.初始化`s`数组。 5.通过遍历`query`,完成求区间`[l,r]`的和。 ## 问题 <div class="tip inlineBlock warning"> 1.为什么要在`alls`中需要`alls.push_back(l);` `alls.push_back(r);`? </div> 首先要明确`alls`中存放的是位置而不是值,也就是存放的是x而不是c。 因为再求区间和的时候,我们提前分析到可以使用前缀和来做,求前缀和就需要下标`l` `r`,如果不加入`l` `r`到`alls`中的话,第`5`步中遍历时`query`就没有办法通过输入的`l` `r`去访问`a`或者`s`。因为`find`函数就是输入映射前的下标,返回在`alls`中的下标`+1`。 举个例子,拿平时的数组来说,下标都是整形,但是如果要求`a[1.5]`肯定是有错误的,在这里也一样。 <div class="tip inlineBlock warning"> 2.为什么要排序和去重? </div> **首先要明确`find`函数的功能,输入一个离散数组的位置(映射前的位置)`x`返回连续数组的位置`+1`(映射后的位置`+1`)。`+1`的目的是为了求区间和时少一步下标为0的判断。** 排序很好理解,因为在`find`函数中是使用了二分来查找`x`在`alls`中的下标`+1`,想要使用二分`alls`就必须具有某种性质这里就可以找一个最简单的办法使他单调(二分!=单调性)。 去重看我下面画的图,图中的例子为本题的样例。(前半部分为在`x`处加`c`后`alls`与`a`中的内容,后半部分为假设不去重求`[3 7]`的区间和) 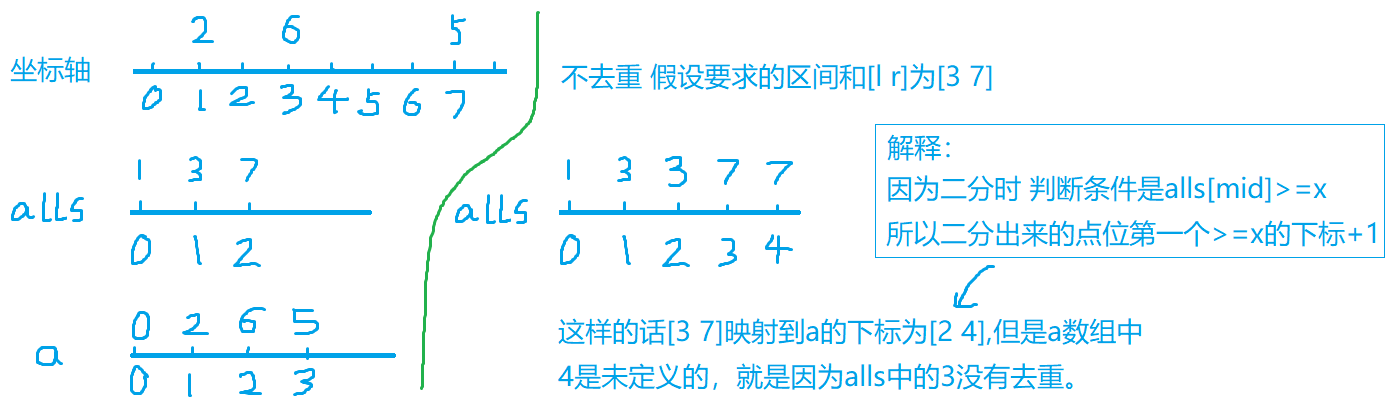 最后修改:2022 年 01 月 06 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏