【数据结构】图论算法_图的遍历

博主： Fivk
发布时间：2021 年 08 月 03 日
1493 次浏览
922字数
分类：数据结构

# 一、深度优先与广度优先遍历

从图中某一顶点出发系统地访问问图中所有顶点，使每个顶点恰好被访问一次，这种运算操作被称为图的遍历。为了避免重复访问某个顶点，可以设一个标志数组 visited[i]，未访问时值为false，访问一次后就改为true。

图的遍历分为深度优先遍历和广度优先遍历两种方法，两者的时间效率都是$O(n^2)$。

### 1.深度优先遍历

深度优先遍历玉深度dfs相似，从一个点A出发，将这个点标为已访问 visited[i]=true；然后再访问所有与之相连，且未被访问过得点。当A的所有邻接点都被访问过后，再退回到A的上一个点（假设是B），再从B的另一个未被访问的邻接点出发，继续遍历。

例如对下图这个无向图深度优先遍历，假定先从1出发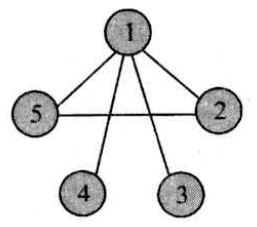

![](https://blog.fivk.cn/usr/uploads/2021/08/787773231.png)

程序以如下顺序遍历：

* 1->2->5，然后退回到2，退回到1.
* 从1开始再访问未被访问过得点3，3没有未访问的邻接点，退回1
* 再从1开始访问未被访问过得节点4，再退回1.
* 起点1的所有邻接点到已访问，遍历结束。

下面给出的深度优先遍历的参考程序，假设图以邻接表存储

```cpp
void dfs(int i)		//图用数组模拟邻接表存储，访问点i
{
	visited[i]=true;		//标记为已经访问过
	for(int j=1;j<=num[i];j++)	//遍历与i相关联的所有未访问过得顶点
	if(!visited[G[i][j]])
	dfs(G[i][j]);
}
```

主程序如下：

```cpp
int main()
{
	...
	memset(visited,false,sizeof(visited));
	for(int i=1;i<=n;i++)、
	if(!visited[i])
	dfs(i);
	/*
	每一个节点都作为起点尝试访问，因为不是从任何
	一点开始都能遍历整个图的，例如
	*/

...
	reutrn 0;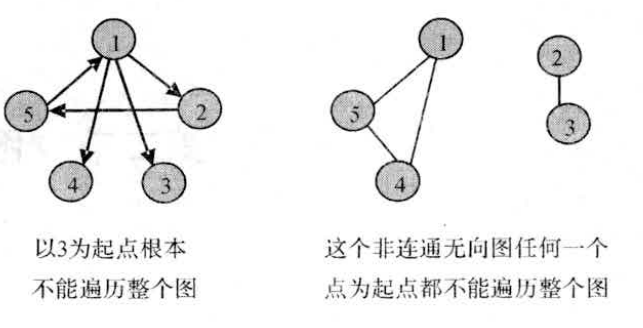
}
```

![](https://blog.fivk.cn/usr/uploads/2021/08/3460106153.png)

### 2.深度优先遍历

广度优先遍历并不常用，从编程复杂度的角度考虑，通常采用的是深度优先遍历。

广度优先遍历和广搜bfs相似，因此使用广度优先遍历一张图并不需要掌握什么新的知识，在原有的广度优先搜索的基础上，做一点小小的修改，就成了广度优先遍历算法。

# 二、一笔画问题

如果一个图存在一笔画，则一笔画的路径叫做欧拉路，如果最后又回到起点，那这个路径叫做欧拉回路。

我们定义奇点是指跟这个点相连的边数目有奇数个点。对于能够一笔画的图，我们有一下两个定理。

* 定理1：存在欧拉路的条件：图是连通的，有且只有2个奇点。
* 定理2：存在欧拉回路的条件：图是连通的，有0个奇点。

两个定理的正确性是显而易见的，既然每条边都要进过一次，那么对于欧拉路，除了起点和和终点外，每个点如果进入了一次，显然一定要出去一次，显然是偶点。对于欧拉回路，每个点进入和出去次数一定都是相等的，显然没有奇点。

求欧拉路的算法很简单，如果寻找欧拉回路，对任意一个点执行深度优先遍历即可。

根据一笔画的两个定理，如果寻找欧拉回路，对任意一个点执行深度优先遍历；找欧拉路，则对一个奇点执行dfs，时间复杂度为$n(m+n)$，m为任意边数，n是点数。

以下是寻找一个图的欧拉路的算法实现：

【输入格式】

第1行n，m，有n个点，m条边，以下m行描述每条边连接的两点。

【输入格式】

欧拉路或欧拉回路

**【输入样例】**

```in
5 5
1 2
2 3
3 4
4 5
5 1
```

【输出样例】

```out
1 5 4 3 2 1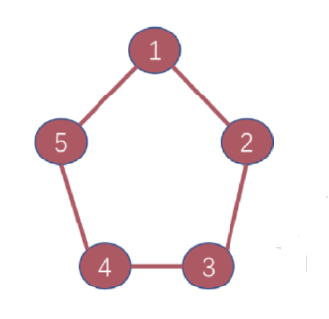
```

![](https://blog.fivk.cn/usr/uploads/2021/08/2167029867.png)

【参考程序】

```cpp
#include <iostream>
#include <cstring>
using namespace std;
#define maxn 101

int g[maxn][maxn];      //此图用邻接矩阵存储
int du[maxn];           //记录每个点的度，就是相连的边的数目
int circuit[maxn];       //用来记录找到的欧拉路的路径
int n,e,circuitpos,i,j,x,y,start;

void find_circuit(int i)    //这个点深度优先遍历过程寻找欧拉路
{
    int j;
    for(j=1;j<=n;j++)
        if(g[i][j]==1)          //从任意一个与他相连的点出发
        {
            g[i][j]=g[j][i]=0;  //删除这条边，避免下一次重复走过
            find_circuit(j);
        }
    circuit[++circuitpos]=i;    //记录下路径
}

int main()
{
    memset(g,0,sizeof(g));
    cin>>n>>e;
    for(i=1;i<=e;i++)
    {
        cin>>x>>y;
        g[x][y]=g[y][x]=1;      //说明x和y间有连边
  
        //统计每个点的度
        du[x]++;
        du[y]++;
    }

/*
    如果有奇点，就从奇点开始寻找，这样找到的就是
    欧拉路，没有奇点就从任意点开始
    这样找到的就是欧拉回路。（因为每一个点都是偶点）
*/

start=1;        
    for(i=1;i<=n;i++)   
        if(du[i]%2==1)  
        start=i;
  
    circuitpos=0;
    find_circuit(start);    //从奇数或任意路开始
    for(i=1;i<=circuitpos;i++)
    cout<<circuit[i]<<" ";
    cout<<endl;

system("pause");
    return 0;
}
```

注意以上程序具有一定的局限性，对于下面这种情况它不能很好的处理：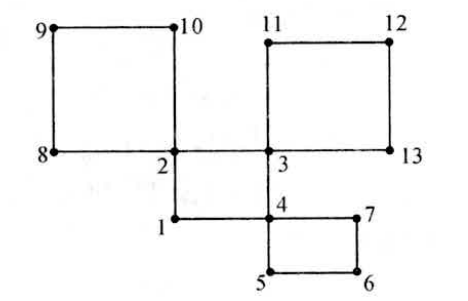

![](https://blog.fivk.cn/usr/uploads/2021/08/986972345.png)

这种具有多个欧拉回路，而本程序只能找到一个回路。

# 三、哈密尔顿环

欧拉回路是指不重复地走过所有路径的回路，而哈密尔顿环是指不重复地走过所有的点，并且最后还能回到起点的回路。
使用简单的深度优先搜索，就能求出一张图中所有的哈密尔顿环。

样例输入:第一行n，m，有n个点，m条边，
以下m行描述每条边连接的两点。

【输入样例】

```cpp
5 7
1 2
1 5
2 3
2 4
2 5
3 4
4 5
```

【输出样例】

```cpp
1 2 3 4 5 1
1 2 4 5 1
1 2 5 1
1 5 2 1
1 5 4 2 1
1 5 4 3 2 1
2 3 4 2
2 3 4 5 2
2 4 3 2
2 4 5 2
2 5 4 2
2 5 4 3 2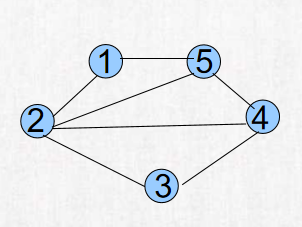
```

![](https://blog.fivk.cn/usr/uploads/2021/08/1447282734.png)

```cpp
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

vector<int> L;
int g[1010][1010];
int x,y,i,j,n,m,T;
bool vis[1010],nodex[1010];

void print(int p)
{
    cout<<p<<" ";
}

void dfs(int last,int t)
{
	vis[t]=true;
    L.push_back(t);
    for(int i=1;i<=n;i++)
    {
        if(g[t][i] && i==T && i!=last)
        {
            L.push_back(i);
            for_each(L.begin(),L.end(),print);
            cout<<endl;
            L.pop_back();
        }

if(g[t][i] && !vis[i] && !nodex[i])
            dfs(t,i);
  
  
    }
    vis[t]=false;
    L.pop_back();
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        g[x][y]=g[y][x]=1;
    }

for(T=1;T<=n;T++)
    {
        if(!nodex[T])
        {
            dfs(0,T); 
            nodex[T]=true;
        }
    }

return 0;
}
```

最后修改：2021 年 09 月 12 日

如果觉得我的文章对你有用，请随意赞赏

【数据结构】图论算法_图的遍历

Fivk • 2021 年 08 月 03 日

# 一、深度优先与广度优先遍历

图的遍历分为深度优先遍历和广度优先遍历两种方法，两者的时间效率都是$O(n^2)$。

### 1.深度优先遍历

例如对下图这个无向图深度优先遍历，假定先从1出发

![](https://blog.fivk.cn/usr/uploads/2021/08/787773231.png)

程序以如下顺序遍历：

下面给出的深度优先遍历的参考程序，假设图以邻接表存储

主程序如下：

...
	reutrn 0;
}
```

![](https://blog.fivk.cn/usr/uploads/2021/08/3460106153.png)

### 2.深度优先遍历

广度优先遍历并不常用，从编程复杂度的角度考虑，通常采用的是深度优先遍历。

# 二、一笔画问题

如果一个图存在一笔画，则一笔画的路径叫做欧拉路，如果最后又回到起点，那这个路径叫做欧拉回路。

我们定义奇点是指跟这个点相连的边数目有奇数个点。对于能够一笔画的图，我们有一下两个定理。

* 定理1：存在欧拉路的条件：图是连通的，有且只有2个奇点。
* 定理2：存在欧拉回路的条件：图是连通的，有0个奇点。

求欧拉路的算法很简单，如果寻找欧拉回路，对任意一个点执行深度优先遍历即可。

以下是寻找一个图的欧拉路的算法实现：

【输入格式】

第1行n，m，有n个点，m条边，以下m行描述每条边连接的两点。

【输入格式】

欧拉路或欧拉回路

**【输入样例】**

```in
5 5
1 2
2 3
3 4
4 5
5 1
```

【输出样例】

```out
1 5 4 3 2 1
```

![](https://blog.fivk.cn/usr/uploads/2021/08/2167029867.png)

【参考程序】

```cpp
#include <iostream>
#include <cstring>
using namespace std;
#define maxn 101

system("pause");
    return 0;
}
```

注意以上程序具有一定的局限性，对于下面这种情况它不能很好的处理：

![](https://blog.fivk.cn/usr/uploads/2021/08/986972345.png)

这种具有多个欧拉回路，而本程序只能找到一个回路。

# 三、哈密尔顿环

样例输入:第一行n，m，有n个点，m条边，
以下m行描述每条边连接的两点。

【输入样例】

```cpp
5 7
1 2
1 5
2 3
2 4
2 5
3 4
4 5
```

【输出样例】

```cpp
1 2 3 4 5 1
1 2 4 5 1
1 2 5 1
1 5 2 1
1 5 4 2 1
1 5 4 3 2 1
2 3 4 2
2 3 4 5 2
2 4 3 2
2 4 5 2
2 5 4 2
2 5 4 3 2
```

![](https://blog.fivk.cn/usr/uploads/2021/08/1447282734.png)

```cpp
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

vector<int> L;
int g[1010][1010];
int x,y,i,j,n,m,T;
bool vis[1010],nodex[1010];

void print(int p)
{
    cout<<p<<" ";
}

if(g[t][i] && !vis[i] && !nodex[i])
            dfs(t,i);
  
  
    }
    vis[t]=false;
    L.pop_back();
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        g[x][y]=g[y][x]=1;
    }

for(T=1;T<=n;T++)
    {
        if(!nodex[T])
        {
            dfs(0,T); 
            nodex[T]=true;
        }
    }

return 0;
}
```

【数据结构】图论算法_图的遍历

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

这是好东西

【Fivk】文章归档

【踩坑日志】mybatis：Caused by: org.apache.ibatis.ognl.ParseException: Encountered " <IDENT> "AND "" at line

【Java】常用类之Arrays

【踩坑日志】java.lang.NullPointerException: null

【C】链表_查找某个节点

【知识总结】使用log4j 2记录Spring Boot应用程序日志

【数据结构】图论算法_图的遍历