Loading... 如图所示,我们把边带有权值的图称为带权图。边的权值可以理解为两点之间的距离。一张图中任意两点中的距离会有不同的路径相连。最短路径就是指相连两点的这些路径中最短的一条。 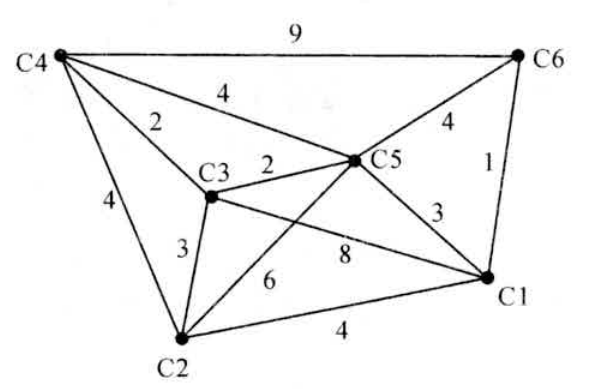 我们有四种算法可以有效地解决最短路径问题。有一点需要读者特别**注意:边的权值可以为负。当出现负边权时,有些算法不适用。** # 一、求出最短路径的长度 <div class="tip inlineBlock success"> 以下没有特别说明的话,dis[u][v]表示从u到v最短路径长度,w[u][b]表示链接u、v的边的长度。 </div> ### 1.Floyed — Warshall 算法 $O(N^3)$ 简称Floyed(弗洛依德)算法,是最简单的最短路径算法,可以计算图中任意两点间的最短路径。Floyed的时间复杂度是$O(N^{3})$,适用于出现负边权的情况。 > 算法描述: > > - (A)初始化: > > 点u、v如果有边相连,则dis[u][v]=w[u][v]。 > > 如果不相连,则dis[u][v]=0x7fffffff。 > > - (B) > > ```cpp > for(k=1;k<n;k++) > for(i=1;i<=n;i++) > for(j=1;j<=n;j++) > if(dis[i][j]>dis[i][k]+dis[k][j]) > dis[i][j]=dis[i][k]+dis[k][j]; > ``` > > - (C)算法结束 > > dis[i][j]得出的就是从i到j的最短路径。 <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-4f9f4db1ca52e37fbdfed42b88dd2a8c95" aria-expanded="true"><div class="accordion-toggle"><span style="">算法分析与解题思想:</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-4f9f4db1ca52e37fbdfed42b88dd2a8c95" class="collapse in collapse-content"><p></p> 三层循环,第一层循环中间点k,第二、第三循环起点终点i、j,算法的思想很容易理解:如果点i到点k的距离加上点k到点j的距离小于原先距离,那么就用这个更短的路径长度来更新原先i到点j的距离。 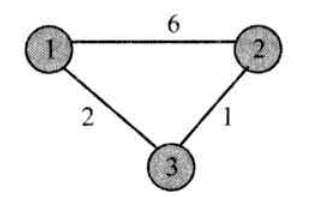 在上图中,因为dis[1][3]+dis[3][2]<dis[1][2],所以就用dis[1][3]+dis[3][2]来更新原先1到2的距离。 我们在初始化时,把不相连的点之间的距离设为一个很大的数,不妨看作这两点相隔很远很远,如果这两点有最短路径的话,就会更新成最短路径的长度。Floyed算法的时间复杂度是$O(N^{3})$。 **Floyed算法变形:** 如果是一个没有边权的图,把相连的两点间的距离设为dis[i][j]=true,不相连的两点设为dis[i][j]=false,用Floyed算法的变形: ```cpp for(k=1;k<=n;k++) for(i=1;i<=n;i++) for(j=1;j<=n;j++) dis[i][j] = dis[i][j]||(dis[i][k] && dis[k][j]) ``` <p></p></div></div></div> 用这个方法可以判断一张图中的两点是否相连。 <div class="tip inlineBlock warning"> 最后再强调一点:用来循环中间点的变量k必须放在最外面一层循环。 </div> ##### 例1 最短路径问题 <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-5eb8b233dd4df8378fbacada45fbb17756" aria-expanded="true"><div class="accordion-toggle"><span style="">题目描述:</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-5eb8b233dd4df8378fbacada45fbb17756" class="collapse in collapse-content"><p></p> **【问题描述】** 平面上有n个点(n<=100),每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。 若有连线,则可以表示从一个点到达另一个点,即两点之间有通路,通路的距离为两点直线的距离。现在的任务是找出从一点到另一点之间的最短路径。 **【输入格式】** 输入文件为 short.in ,共 n+m+3 行中: 第一行为整数 n。 第二行到第 n+1 行(共 n 行),每行连个整数 x 和 y 描述了一个点的坐标。 第 n+2 行为一个整数m,表示图中连线的个数。 此后的m行,每行描述一条线段,由两个整数 i 和 j 组成,表示第i个点和第j个点之间有连线。 最后一行:两个整数 s 和 t ,分别表示源点和目标点。 **【目标格式】** 输出文件为short.out,仅一行,一个实数(保留两位小数),表示从 s 到 t 的最短路径长度。 **【输入样例】** ```cpp 5 0 0 2 0 2 2 0 2 3 1 5 1 2 1 3 1 4 2 5 3 5 1 5 ``` **【输出样例】** ```cpp 3.14 ``` **【参考程序】** ```cpp #include <iostream> #include <cmath> #include <cstring> using namespace std; double f[101][101]; int a[101][2]; int s,t,n,m,x,y; int main() { cin>>n; memset(f,0x7f,sizeof(f)); for(int i=1;i<=n;i++) { cin>>a[i][0]>>a[i][1]; } cin>>m; for(int i=1;i<=m;i++) { cin>>x>>y; f[x][y]=f[y][x]=(double)sqrt(pow(a[x][0]-a[y][0],2)+pow(a[x][1]-a[y][1],2)); } for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(f[i][j]>f[i][k]+f[k][j]) f[i][j]=f[i][k]+f[k][j]; cin>>s>>t; cout<<f[s][t]<<endl; return 0; } ``` <p></p></div></div></div> ##### 例2 牛的旅行 <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-55ab07d6513f7f6f6c5b428c8d8f43cc23" aria-expanded="true"><div class="accordion-toggle"><span style="">题目描述:</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-55ab07d6513f7f6f6c5b428c8d8f43cc23" class="collapse in collapse-content"><p></p> **【问题描述】** 农名John的农场里有很多牧区。有的路径链接一些特定的牧区。一片所有连通的牧区称为一个牧场。但是就目前而言,你能看到至少有两个牧区不连通。现在,John像在农场里添加一条路径(注意,恰好一条)。对这条路径有这样的限制:一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短距离的距离)。考虑如下的两个牧场,图中有5个牧场,牧区用“*”表示,路径用直线表示,每一个牧区都有自己的坐标: 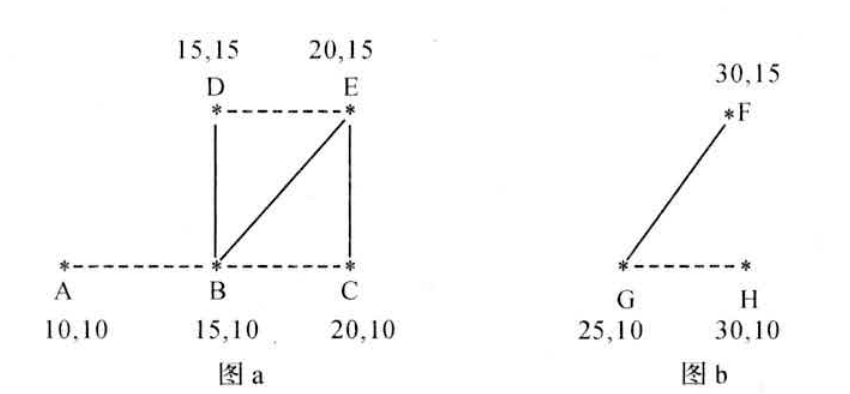 如图所示,的牧场的直径大约是12.07106,最远的连个牧场是 A 和 E ,他们之间的最短路径是A-B-E。 这两个牧场都在John的农场上。John将会在两个牧场中各选一个牧区,然后用一条路径连起来,使得连通后这个新的更大的农场有最小的直径。注意,如果两条路径中途相交,我们不认为他们是连通的。只有两条路径在同一各牧区相交,我们才认为它们是连通的。 现在请你编程找出一个链接两个不同牧场的路径,使得连上这条路径后,这个更大的新牧场有最小路径。 **【输入格式】** 第 1 行:一个整数N (1 <= N <= 150), 表示牧区数; 第 2 到 N+1 行:每行两个整数X,Y ( 0 <= X,Y<= 100000 ), 表示N个牧区的坐标。每个牧区的坐标都是不一样的。 第 N+2 行到第 2*N+1 行:每行包括N个数字 ( 0或1 ) 表示一个对称邻接矩阵。 例如,题目描述中的两个牧场的矩阵描述如下: A B C D E F G H A 0 1 0 0 0 0 0 0 B 1 0 1 1 1 0 0 0 C 0 1 0 0 1 0 0 0 D 0 1 0 0 1 0 0 0 E 0 1 1 1 0 0 0 0 F 0 0 0 0 0 0 1 0 G 0 0 0 0 0 1 0 1 H 0 0 0 0 0 0 1 0输入数据中至少包括两个不连通的牧区。 **【输出格式】*** 只有一行,包括一个实数,表示所求答案。数字保留六位小数。 **【输入样例】** ```cpp 8 10 10 15 10 20 10 15 15 20 15 30 15 25 10 30 10 01000000 10111000 01001000 01001000 01110000 00000010 00000101 00000010 ``` **【输出样例】** ```cpp 22.071068 ``` **【算法分析】** 用Floyed算法求出任意两点间的最短距离,然后求出每个点到所有可达到的点的最大距离,做记录mids[i]。 r1=max(mdis[i]) 然后枚举不连通的两点i、j,把它们连通,则新的直径是 mdis[i]+mids[j]+(i,j)间的距离。 r2=min(mdis[i]+mdis[j]+dis[i,j]) re=max(r1,r2); re就是所求。 **【参考程序】** ```cpp #include <iostream> #include <cstring> #include <cmath> #include <cstdio> using namespace std; int a[151][3]; double g[151][151],mdis[151],r1=0,r2=1e12; int n,x,y,i,j,k; int main() { cin>>n; for(i=1;i<=n;i++) //输入坐标 cin>>a[i][1]>>a[i][2]; for(i=1;i<=n;i++) //计算距离 { for(j=1;j<=n;j++) { char ch; cin>>ch; if(ch=='1') g[i][j]=(double)sqrt(pow(a[i][1]-a[j][1],2)+pow(a[i][2]-a[j][2],2)); else g[i][j]=1e12; } } //Floyed计算最短距离 for(k=1;k<=n;k++) for(i=1;i<=n;i++) for(j=1;j<=n;j++) if((i!=j&&i!=k&&k!=j)&&(g[i][k]<r2&&g[k][j]<1e12)&&(g[i][k]+g[k][j]<g[i][j])) g[i][j]=g[i][k]+g[k][j]; //求mdis[i] for(i=1;i<=n;i++) { for(j=1;j<=n;j++) if(mdis[i]<g[i][j]&&g[i][j]<1e12) mdis[i]=g[i][j]; } //求r1 for(i=1;i<=n;i++) if(r1<mdis[i]) r1=mdis[i]; //求r2 for(i=2;i<=n;i++) for(j=1;j<i;j++) if(g[i][j]==1e12) if(r2>mdis[i]+mdis[j]+(double)sqrt(pow(a[i][1]-a[j][1],2)+pow(a[i][2]-a[j][2],2))) r2=mdis[i]+mdis[j]+(double)sqrt(pow(a[i][1]-a[j][1],2)+pow(a[i][2]-a[j][2],2)); if(r1>r2) r2=r1; printf("%.6lf",r2); return 0; } ```  <p></p></div></div></div> ### 2.Dijkstra 算法 $O(N^2)$ 用来计算从一个点到其他所有点的最短路径的算法,是一种单源最短路径算法。也就是说,只能计算起点只有一个的情况。 Dijkstra 的时间复杂度是$O(N^2)$,它不能处理存在负边权的情况。 算法描述: 设起点为 s,dis[v]表示从s到v的最短路径,pre[v]为v的前驱结点,用来输出路径。 (a) 初始化:dis[v]=∞($v\neq s$);dis[s]=0;pre[s]=0; (b) `for(i=1;i<=n;i++)` 1. 在没有被访问过的点中找一个顶点u使得dis[u]是最小的。 2. u标记为已确定最短路径。 3. for 与 u 相连的每个未确定最短路径的顶点v。 ```cpp if(dis[u]+w[u][v]<dis[v]) { dis[v]=dis[u]+w[u][v]; pre[v]=u; } ``` (c) 算法结束:dis[v]为 s 到 v 的最短距离;pre[v]为v的前驱结点,用来输出路径。 **算法分析 与 解题思路:** 从起点到一个点的最短路径一定会经过至少一个“中转点”(例如图中1到5的最短路径,中转点是2。特殊的,我们认为1也是一个“中转点”)。显而易见,如果我们想求出起点到一个点的最短路径,那我们必然要先求出中转点的最短路径(例如我们必须先求出2的最短路径后,才能求出起点到5的最短路径)。 换句话说,如果起点1到某处一点 $v_0$ 的最短路径 $v_i$ ,那么中转点 $v_i$ 一定是先于 $v_0$ 被确定了最短路径的点。 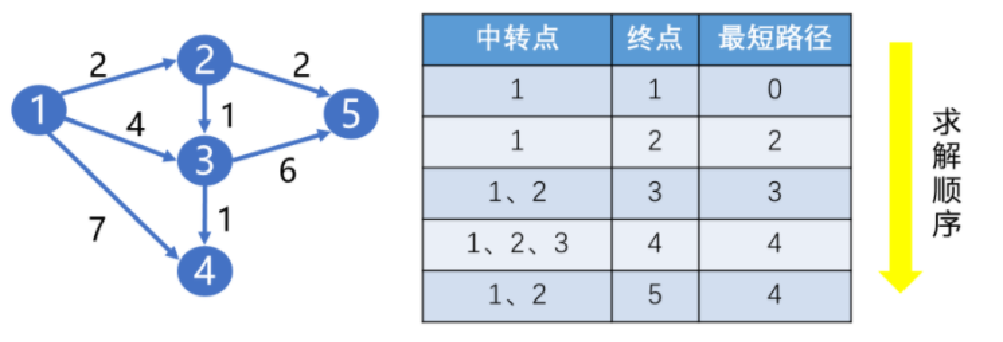 我们把点分成两类,一类是已确定最短路径的点,称为“白点”,另一类是未确定最短路径的点,称为“蓝点”。如果我们要求出一个点的最短路径,就是要把这个点由蓝点变为白点。从起点到蓝点的最短路径上的中转点在这个时刻只能是白点。 Dijkstra 的算法思想,就是一开始将起点到起点的距离标记为0,而后进行n此循环,每次找出一个到起点距离dis[u]最短的点 u,将它从蓝点变为白点。随后枚举所有的蓝点 $v_i$,如果以此白点为中转到蓝点$v_i$的路径dis[u]+w[u][$v_i$]更短的话,将它最为$v_i$的“更短路径”dis[v] (此时还不能确定是不是$v_i$的最短路径)。 就这样,我们每找到一个白电,就尝试着用它修改其他所有的蓝点。中转点先于终点变成白点,故每一个终点一定能够被它的**最后一个**中转点所修改,而求得最短路径。 让我们对以上这段枯燥的文字做一番模拟,加深理解。 算法开始时,作为起点的dis[1]=0,其他的点dis[i]=0x7fffffff。 已经确定最短路径的点标黄点,未确定最短路径的点标为蓝点。 - 第一轮循环从1号点开始,对所有蓝点做出修改。  - 第二轮循环找到dis[2]最小,将2变为黄点,对所有蓝点做出修改  - 第三轮循环找到dis[3]最小,将3变为黄点,对所有蓝点做出修改 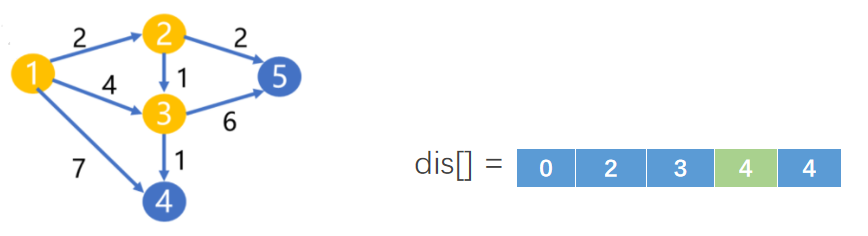 - 第四轮循环找到dis[4]最小,将4变为黄点,对所有蓝点做出修改 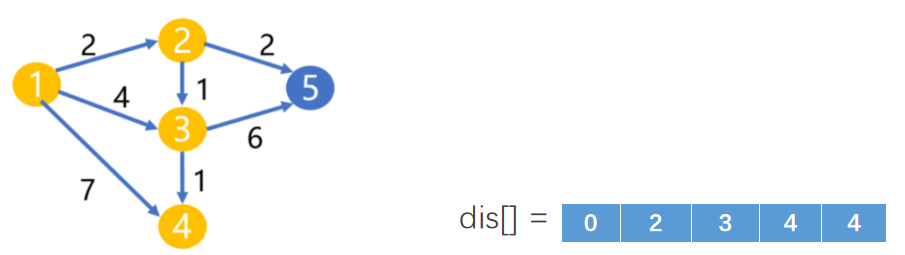 - 第五轮循环找到dis[5]最小,将5变为黄点,对所有蓝点做出修改 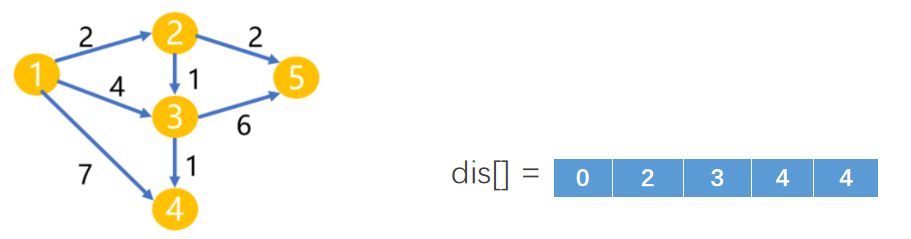 **Dijkstra 无法处理负边权的情况:** 例:如图 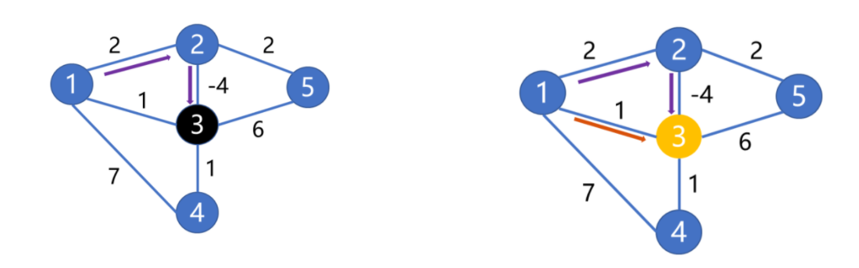 2到3的边权值为-4,显然从起点1到3的最短路径时-2 (1-2-3),但是 Dijkstra 在第二轮循环开始就会找当前dis[i]最小的点3,并标记它为白点。 这时的dis[3]=1,然而1却不是从起点到点3的最短路径。应为3已经被标记为白点,最短路径值 dis[3] 不会再被修改了,所以我们在边权存在负数的情况下得到了错误的答案! ##### 例3 最短路径问题(Dijkstra) 题目参见 **Floyed算法** ,这里用 Dijkstra 算法解决。 <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-86f15ea4f242d212e532fb994bae73483" aria-expanded="true"><div class="accordion-toggle"><span style="">题目描述:</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-86f15ea4f242d212e532fb994bae73483" class="collapse in collapse-content"><p></p> **【问题描述】** 平面上有n个点(n<=100),每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。 若有连线,则表示可从一个点到达另一个点,即两点间有通路,通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径。 **【输入格式】** 第一行为整数n。 第2行到第n+1行(共n行) ,每行两个整数x和y,描述了一个点的坐标。 第n+2行为一个整数m,表示图中连线的个数。 此后的m 行,每行描述一条连线,由两个整数i和j组成,表示第i个点和第j个点之间有连线。 最后一行:两个整数s和t,分别表示源点和目标点。 **【输出格式】** 输出仅一行,一个实数(保留两位小数),表示从s到t的最短路径长度。 【输入样例】 ```cpp 5 0 0 2 0 2 2 0 2 3 1 5 1 2 1 3 1 4 2 5 3 5 1 5 ``` **【样例输出】** ```cpp 3.14 ``` **【参考程序】** ```cpp #include <iostream> #include <cstdio> #include <cstring> #include <cmath> using namespace std; int a[101][3]; double c[101]; bool b[101]; double f[101][101]; int n,i,j,k,x,y,m,s,e; double minl; double maxx=1e30; int main() { cin>>n; for(i=1;i<=n;i++) cin>>a[i][1]>>a[i][2]; for(i=1;i<=n;i++) for(j=1;j<=n;j++) f[i][j]=maxx; //初始化数组最大值 cin>>m; for(i=1;i<=m;i++) //预处理 x、y 间距离 f[x][y] { cin>>x>>y; f[x][y]=f[y][x]=sqrt(pow(double(a[x][1]-a[y][1]),2)+pow(double(a[x][2]-a[y][2]),2)); } cin>>s>>e; memset(b,false,sizeof(b)); // Dijksra 最短路 b[s]=true; c[s]=0; for(i=1;i<=n;i++) c[i]=f[s][i]; for(i=1;i<=n-1;i++) { minl=maxx; k=0; for(j=1;j<=n;j++) //查询可更新的点 if( (!b[j]) && (c[j]<minl) ) { minl=c[j]; k=j; } if(k == 0) break; b[k]=true; for(j=1;j<=n;j++) if(c[j]>c[k]+f[k][j]) c[j]=c[k]+f[k][j]; } printf("%.2lf\n",c[e]); system("pause"); return 0; } ``` <p></p></div></div></div> ##### 例4 最小花费 <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-380a5639092e58b8c6e75c27e3e1aca372" aria-expanded="true"><div class="accordion-toggle"><span style="">题目描述:</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-380a5639092e58b8c6e75c27e3e1aca372" class="collapse in collapse-content"><p></p> **【问题描述】** 在n个人中,某些人的银行账号之间可以互相转账。这些人之间转账的手续费各不相同。给定这些人之间转账时需要从转账金额里扣除百分之几的手续费,请问A最少需要多少钱使得转账后B收到100元。 **【输入格式】** 第一行输入两个正整数n,m,分别表示总人数和可以互相转账的人的对数。 以下m行每行输入三个正整数x,y,z,表示标号为x的人和标号为y的人之间互相转账需要扣除z%的手续费 (z<100)。 最后一行输入两个正整数A,B。数据保证A与B之间可以直接或间接地转账。 **【输出格式】** 输出A使得B到账100元最少需要的总费用。精确到小数点后8位。 **【输入样例】** ```in 3 3 1 2 1 2 3 2 1 3 3 1 3 ``` **【输出样例】** ```out 103.07153164 ``` **【数据规模】** 1<=n<=2000 **【参考程序】** ```cpp #include <iostream> #include <cstring> using namespace std; bool b[2001]; double f[2001][2001],dis[2001]; double maxn,z; int x,y,A,B,m,n,i,j,k; void init(); //初始化 void Dijkstra(int A); //算法 int main() { init(); Dijkstra(A); printf("%.8lf\n",100/dis[B]); system("pause"); return 0; } void init() { //数据初始化 cin >> n >> m; for(i=1;i<=m;i++) { cin >> x >> y >>z; f[x][y] = f[y][x] = double(100.0 - z)/100.0; } cin >> A >> B; //路线不用初始化为无穷,因为这个题有点特殊,不能转账就是全损,汇率为0 } void Dijkstra(int A) { for(i = 1;i <= n;i++) dis[i] = f[A][i]; b[A] = true; dis[A] = 1; //自己给自己转账没有损耗,汇率为1 for(i = 1;i <= n - 1;i++) { maxn = 0; //这里我们是要寻找最大值,这样才能让答案为最小 k = 0; for(j = 1;j <= n;j++) if(!b[j] && dis[j]>maxn) // Dijkstra 寻找最小权重 { k = j; maxn = dis[j]; } if(k == B || k == 0) break; else b[k]=true; for(j=1;j<=n;j++) if(!b[j] && dis[j] < dis[k] * f[k][j]) //优化为最大的数值,保证损耗最小 dis[j] = dis[k] * f[k][j]; } } ``` <p></p></div></div></div> ##### 数据结构课程案例 in: ```in 5 10000 10 10000 30 100 10000 10000 50 10000 10000 10000 10000 10000 10000 10 10000 10000 20 10000 60 10000 10000 10000 10000 10000 ``` code: ```c #include <stdio.h> #define N 20 typedef struct { int w; // 权值 int p,t; // 前驱, 标记 (0:未选定, 1:已选定) }RT; void Dijkstra(int a[N][N], int n, RT r[]) { int i, j, m; r[0].w = 0; r[0].p = -1; r[0].t = 1; // 0节点初始化 for (int i = 1; i < n; i++) // 初始化 ,链接与0相连的节点 { r[i].w = a[0][i]; r[i].p = 0; r[i].t = 0; } for (j = 1; j < n; j++) { for (i = 1; i < n; i++) { if (r[i].t == 0) // 找到第一个未被标记的点 (作为擂台擂主) { m = i; break; } } // 找到最小边 for (i++; i < n; i++) // 与擂主比较,找到最小的下标 m if (r[i].t == 0 && r[i].w < r[m].w) m = i; r[m].t = 1; // 找到最小后标记为 1, 表示已经作为转接点了 // 修改其余边 for (i = 1; i < n; i++) { if ((r[i].t == 0) && r[m].w + a[m][i] < r[i].w) { r[i].w = r[m].w + a[m][i]; r[i].p = m; } } } } int main() { int a[N][N]; RT r[N]; int i, j, n; int flag = 0; scanf("%d",&n); for (i = 0; i < n; i++) for (j = 0; j < n; j++) scanf("%d",&a[i][j]); Dijkstra(a, n, r); for (int i = 0; i < n; i++) { printf("%d ",r[i].w); for (j = i; j != -1; j = r[j].p) printf("%d <-",j); printf("\n"); } return 0; } ``` ### 3.Bellman — Ford 算法 $O(NE)$ 贝尔曼 - 福特(Bellman-Ford)算法是一种在图中求解最短路径问题的算法。最短路径问题就是在加权图指了起点和终点的前提下,寻找从起点到终点的路径中权重总和最小的那条路径。 **Bellman-Ford算法能够处理存在负边权的情况,但无法处理存在负权回路的情况。** **【算法实现】** 将图的顶点数设为 n、边数设为 m,我们来思考一下贝尔曼 - 福特算法的时间复杂度是多少。该算法经过 n 轮更新操作后就会停止,而在每轮更新操作中都需要对各个边进行1 次确认,因此 1 轮更新所花费的时间就是 O(m),整体的时间复杂度就是 O(nm)。 设s为起点,dis[v]即为s到v的最短距离,pre[v]为v前驱。w[j]是边j的长度,且j连接u、v。 初始化:dis[s]=0,dis[v]=∞(v≠s),pre[s]=0 ```cpp for (i = 1; i <= n-1; i++) for (j = 1; j <= E; j++) //注意要枚举所有边,不能枚举点。 if (dis[u]+w[j]<dis[v]) //u、v分别是这条边连接的两个点。 { dis[v] =dis[u] + w[j]; pre[v] = u; } ``` **【算法步骤】** > 1. 初始化时将起点s到各个顶点v的距离dist(s->v)赋值为∞,dist(s->s)赋值为0。 > 2. 后续进行最多n-1次遍历操作(n为顶点个数),对所有的边进行**松弛操作**。所谓的松弛,以边ab为例,若dist(a)代表起点s到达a点所需要花费的总数, dist(b)代表起点s到达b点所需要花费的总数,weight(ab)代表边ab的权重, 若存在:(dist(a) +weight(ab)) < dist(b) > 则说明存在到b的更短的路径,s->...->a->b,更新b点的总花费为(dist(a) +weight(ab)),父节点为a(也就是b的前驱为a)。 <div class="tip inlineBlock warning"> 说明:每次松弛操作实际上是对相邻节点的访问,由于图的最短路径最长不会经过超过n-1条边,所以最多n-1次遍历操作可得到最短路径。 </div> **【负权回路】** > 虽然贝尔曼 - 福特算法可以求出存在负边权情况下的最短路径,却无法解决存在负权回路的情况。 > > 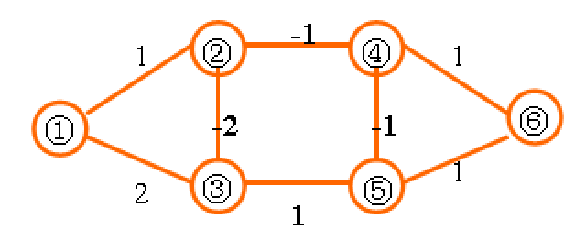 > > 负权回路是指边权之和为负数的一条回路,上图中②-④-⑤-③-②这条回路的边权之和为-3。在有负权回路的情况下,从1到6的最短路径是多少?答案是无穷小,因为我们可以绕这条负权回路走无数圈,每走一圈路径值就减去3,最终达到无穷小。 > 所以说存在负权回路的图无法求出最短路径,贝尔曼 - 福特算法可以在有负权回路的情况下输出错误提示。 > 如果在Bellman-Ford算法的两重循环完成后,还是存在某条边使得:dis[u]+w<dis[v],则存在负权回路: > > for每条边(u,v) > if (dis[u]+w<dis[v]) return False **【算法图解】** > 5个顶点,5条边,5个边权,求顶点1到其他各个点最小值 > > 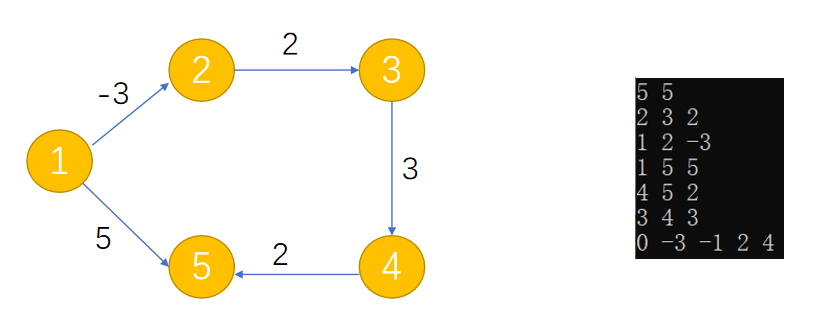 > > 1. 初始化:将dis[s] = 0,dis[其他] = ∞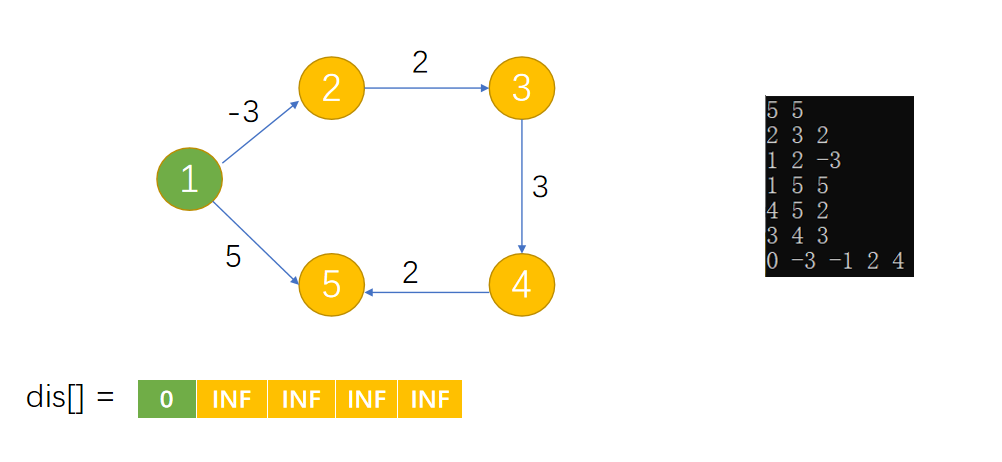 > 2. 第一轮松弛操作:将与s相连的点读入边权(并不代表是最短)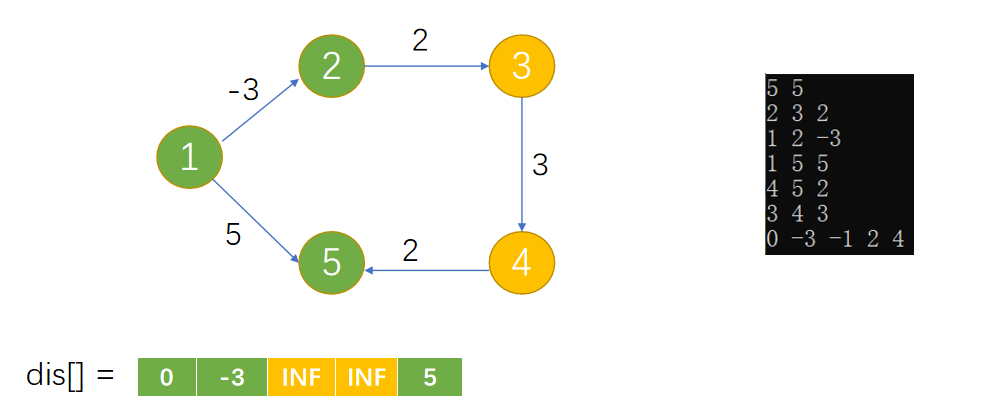 > 3. 第二轮松弛操作:继续延申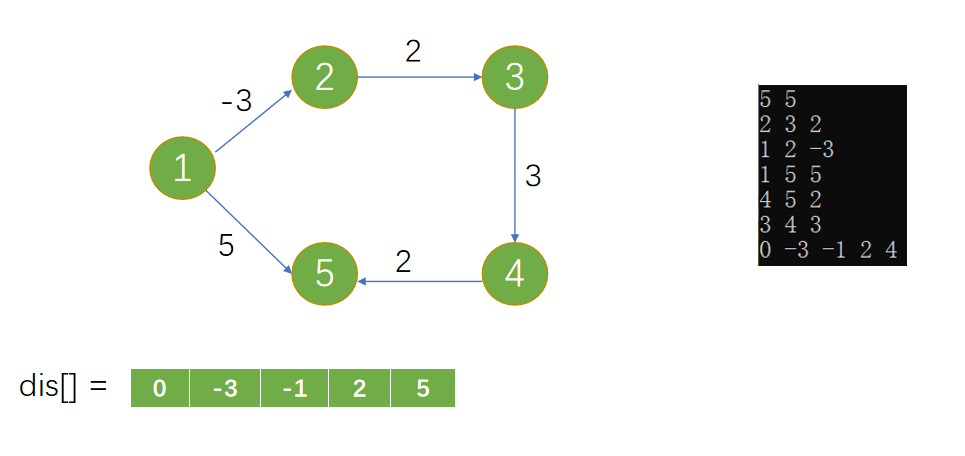 > 4. 第三轮松弛操作:优化最短路径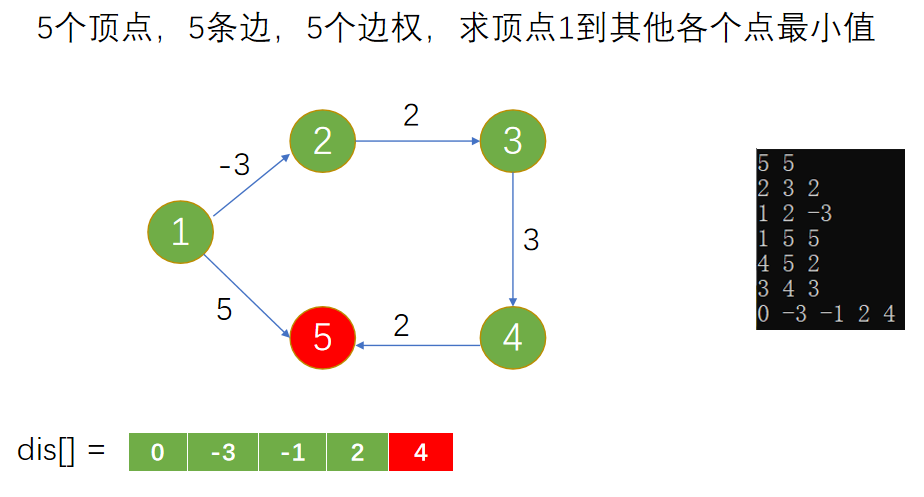 > 5. 第四轮松弛操作:继续判断,但在这里没有变化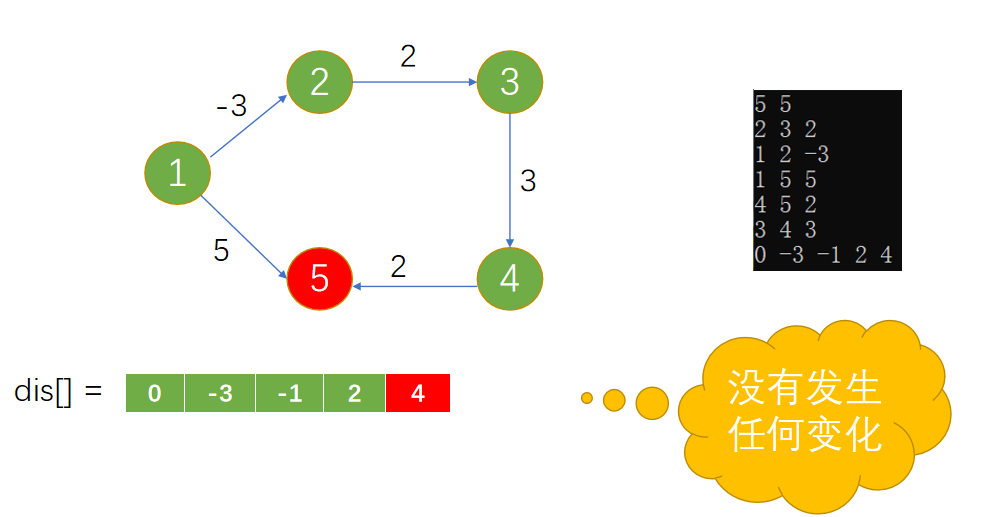 ##### 例5 最短路径问题(Bellman — Ford) <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-e7f1cfa944bc8525fb566d044d75334e66" aria-expanded="true"><div class="accordion-toggle"><span style="">题目描述:</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-e7f1cfa944bc8525fb566d044d75334e66" class="collapse in collapse-content"><p></p> **【问题描述】** 平面上有n个点(n<=100),每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。 若有连线,则表示可从一个点到达另一个点,即两点间有通路,通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径。 **【输入格式】** 第一行为整数n。 第2行到第n+1行(共n行) ,每行两个整数x和y,描述了一个点的坐标。 第n+2行为一个整数m,表示图中连线的个数。 此后的m 行,每行描述一条连线,由两个整数i和j组成,表示第i个点和第j个点之间有连线。 最后一行:两个整数s和t,分别表示源点和目标点。 **【输出格式】** 输出仅一行,一个实数(保留两位小数),表示从s到t的最短路径长度。 **【输入样例】** ```cpp 5 0 0 2 0 2 2 0 2 3 1 5 1 2 1 3 1 4 2 5 3 5 1 5 ``` **【输出样例】** ```cpp 3.41 ``` **【参考程序】** ```cpp #include <iostream> #include <cstdio> #include <cmath> #include <cstring> using namespace std; double a[101][3],dis[1001],w[1001]; int n,m,u[101],v[101],s,t; bool b[101]; int main() { cin >> n; // n个点 for(int i = 1;i <= n;i++) cin >> a[i][1] >> a[i][2]; // 读入坐标 cin >> m; for(int i = 1;i <= n;i++) { //输入两点,得到两点的权值 cin >> u[i] >> v[i]; w[i] = sqrt(pow(a[u[i]][1] - a[v[i]][1], 2) + pow(a[u[i]][2] - a[v[i]][2], 2)); //w[i] 是两点之间的距离 } cin >> s >> t; memset(dis,0x7f,sizeof(dis)); dis[s] = 0; // Bellman 算法主体 for(int i = 1;i <= n-1;i++) { for(int j = 1;j <= m;j++) { if(dis[v[j]] > dis[u[j]] + w[j]) dis[v[j]] = dis[u[j]] + w[j]; if(dis[u[j]] > dis[v[j]] + w[j]) dis[u[j]] = dis[v[j]] + w[j]; } } printf("%.2lf\n",dis[t]); system("pause"); return 0; } ``` <p></p></div></div></div> ### 4.SPFA 算法$O(KE)$ SPFA(Shortest Path Faster Algorithm)算法是求单源最短路径的一种算法,它是Bellman-ford的队列优化,它是一种十分高效的最短路算法。 很多时候,给定的图存在负权边,这时类似Dijkstra等算法便没有了用武之地,而Bellman-Ford算法的复杂度又过高,SPFA算法便派上用场了。SPFA的复杂度大约是O(kE),E是边数,K是常数,平均值为2。 **【主要思想】** 初始时将起点加入队列。每次从队列中取出一个元素,并对所有与它相邻的点进行修改,若某个相邻的点修改成功,则将其入队。直到队列为空时算法结束。 这个算法,简单的说就是队列优化的bellman-ford,利用了每个点不会更新次数太多的特点发明的此算法。 SPFA 在形式上和广度优先搜索非常类似,不同的是广度优先搜索中一个点出了队列就不可能重新进入队列,但是SPFA中一个点可能在出队列之后再次被放入队列,也就是说一个点修改过其它的点之后,过了一段时间可能会获得更短的路径,于是再次用来修改其它的点,这样反复进行下去。 此外,SPFA算法还可以判断图中是否有负权环,即一个点入队次数超过N。 通过下面的图我们看一下,SPFA算法的整个过程。 **【算法图解】** 5个顶点,7条边,7个边权,求顶点1到其他各个点最小值 > 1. 第一步: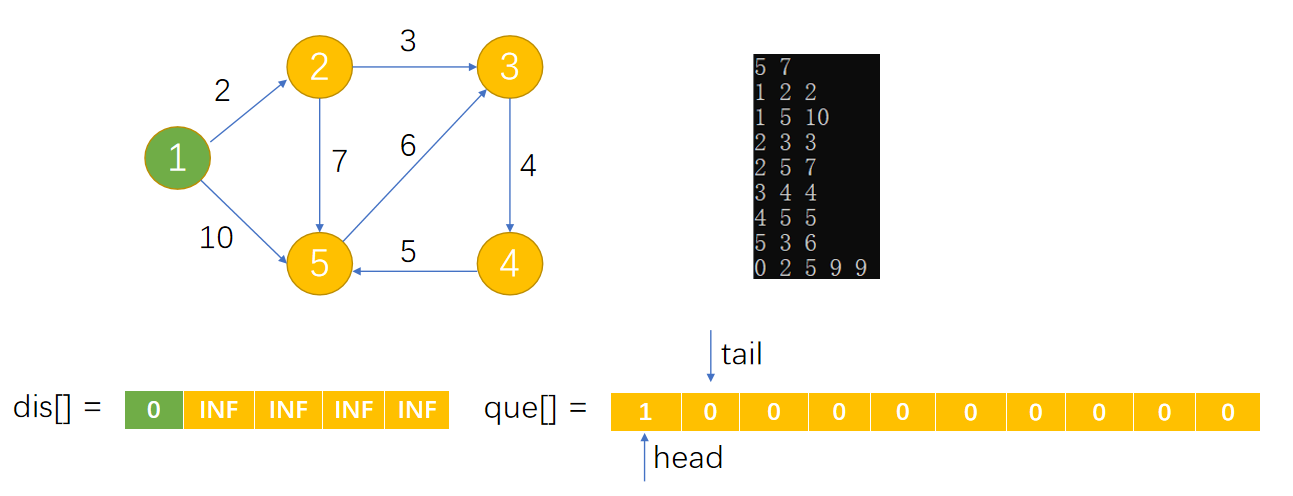 > 2. 第二步: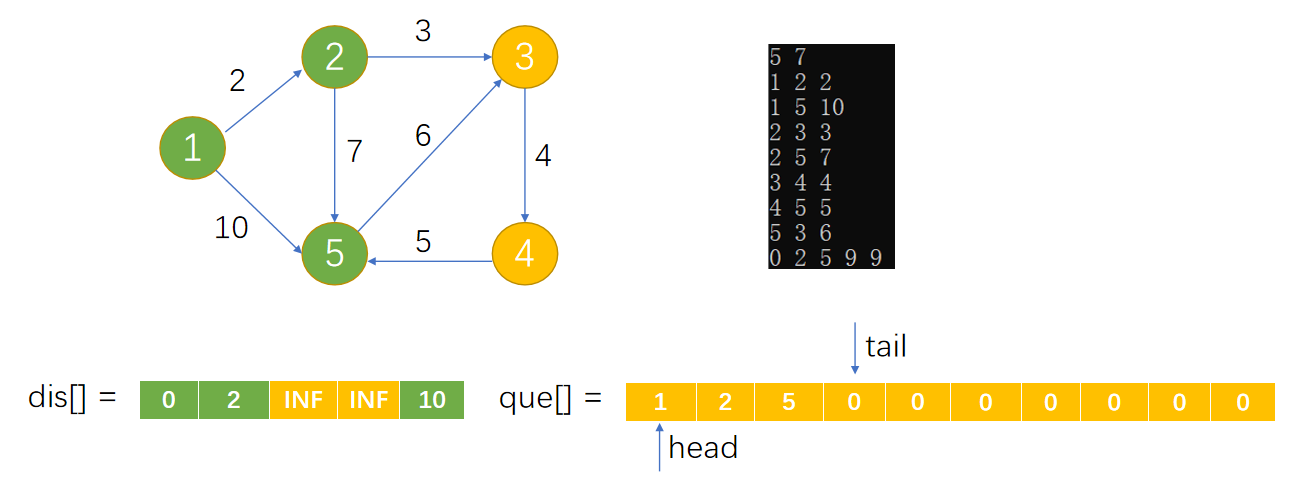 > 3. 第三步: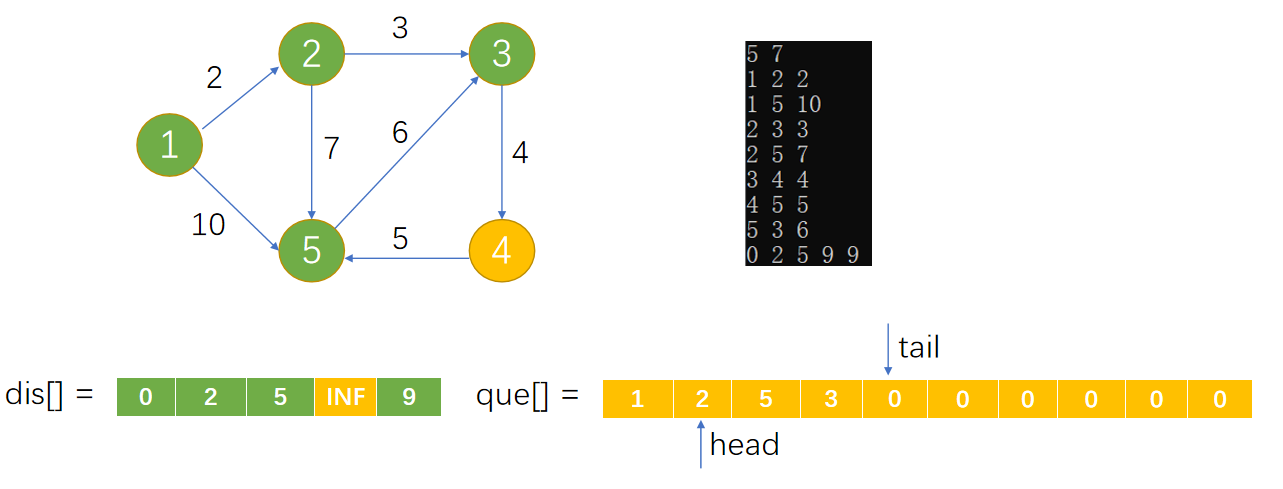 > 4. 第四步: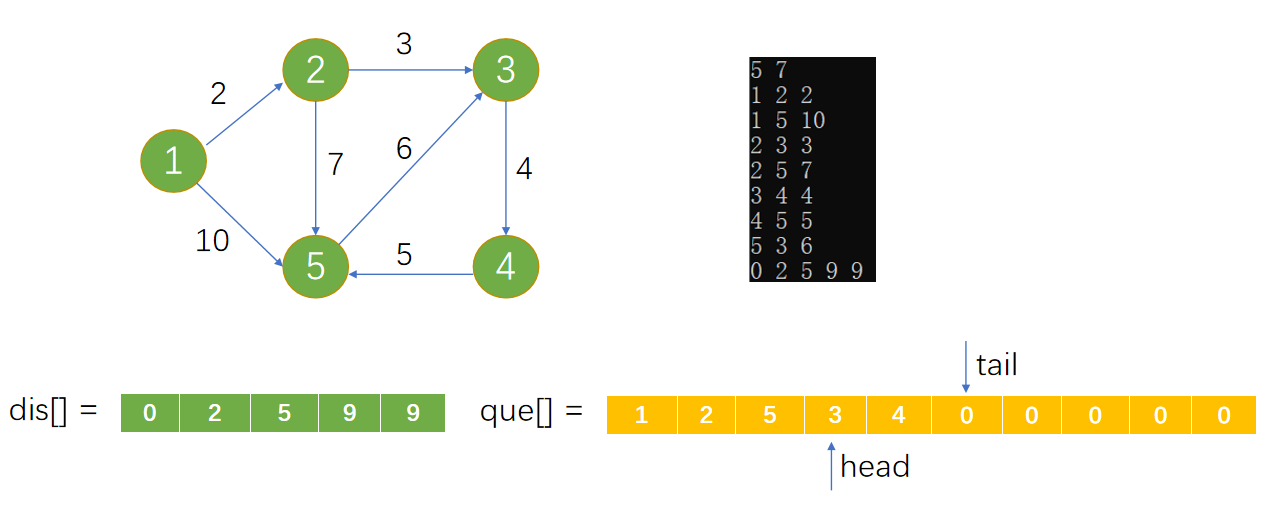 > 5. 第五步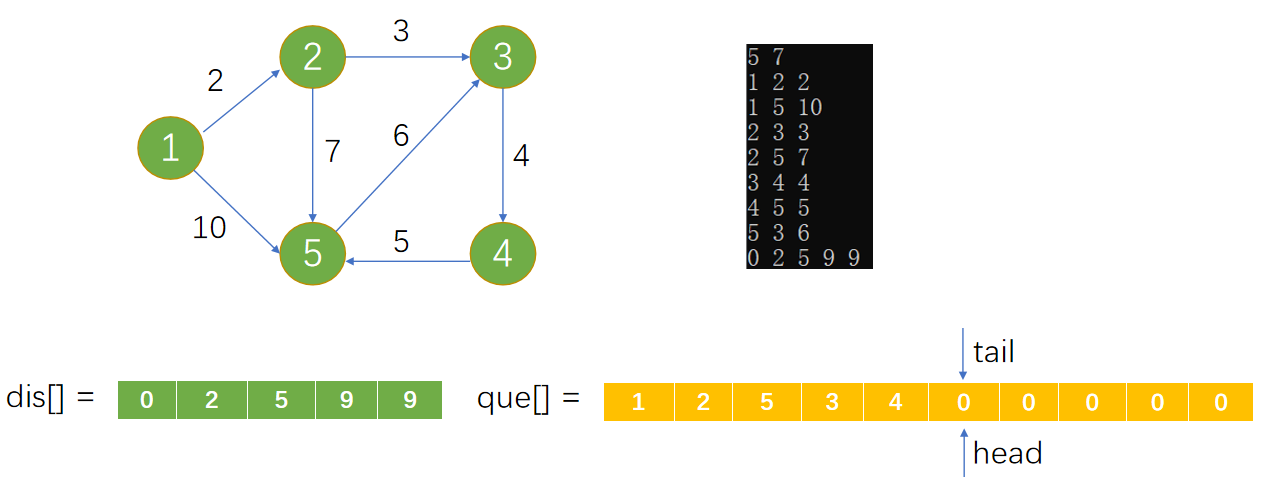 **【算法实现】** dis[i]记录从起点 s 到 i 的最短路径,w[i][j] 记录连接 i、j 的边的长度,pre[v] 记录前趋。team[1……n] 为队列,头指针head,尾指针tail。 布尔数组 exist[i……n] 记录一个点是否在队列中。 初始化:dis[s] = 0, dis[v] = ∞ ($ v\neq s$), `memset(exist,false,sizeof(exist))`; 起点队列 team[1] = s; head = 0; tail =1; exist[s] = true; ```cpp do { 1.头指针向下移一位,取出指向的点u。 2.exist[u] = false; //表示已被取出队列 3.for 与 u 相连的所有点 v //注意不要去枚举所有点,用数组模拟邻接表存储 if(dis[v] > dis[u] + w[u][v]) { dis[v] = dis[u] + w[u][v]; pre[v] = u; if(!exist[v]) //如果队列中没有v,则v入队 { 尾指针下移一位,原来位置还给v; exist[v] = true; } } }while(head < tail); ``` <div class="tip inlineBlock success"> 循环队列: 采用循环队列能够降低队列大小,队列长度只需要开到$2*n+5$即可。 例题中的参考程序采用了循环队列。 </div> ##### 例6 最短路径问题(SPFA) <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-496c19106fb3e0361e00c5e8b016c31277" aria-expanded="true"><div class="accordion-toggle"><span style="">题目描述:</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-496c19106fb3e0361e00c5e8b016c31277" class="collapse in collapse-content"><p></p> **【问题描述】** 平面上有n个点(n<=100),每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。 若有连线,则表示可从一个点到达另一个点,即两点间有通路,通路的距离为两点间的直线距离。现在的任务是找出点1与其他点的距离 **【输入格式】** 第一行为整数n,m。 此后的m 行,每行描述一条连线,由两个顶点u、v还有边权w组成。 **【输出格式】** 输出仅一行,n个实数,表示点1到其他点的距离 **【输入样例】** ```in 5 7 1 2 2 1 5 10 2 3 3 2 5 7 3 4 4 4 5 5 5 3 6 ``` **【输出样例】** ```cpp 0 2 5 9 9 ``` **【参考程序】** ```cpp #include <iostream> #include <cstring> #include <queue> using namespace std; const int INF = 0x7fffffff; struct Edge // 声明一个结构体,作为连接表 { //边的结构体 int next; // 下条边的标号 int to; // 这条边到达的点 int w; // 这条边的权重 }edge[101]; int n,m; // n个顶点,m条边 int num_edge = 0; // 序号 int head[101],dis[101]; // head[] 保存的是顶点 bool b[101]; // 标记是否已经入队 queue<int> que; void add_edge(int from, int to, int w); // 添加边(创建连接表),参数分别是(边的起点,边的终点,边的权重) int main() { cin >> n >> m; memset(dis,0x7f,sizeof(dis)); dis[1] = 0; // 依题意,表示从1开始,计算点1到其他的距离 // 题目给的点,和有向图有关,不会出错的 //建立连接表 for(int i = 1;i <= m;i++) { int from, to, w; cin >> from >> to >> w; add_edge(from, to, w); //add_edge(to, from, w); 无向图就再加上这句(相信认真看前面的,这里没问题) } que.push(1); b[1] = true; // 从点1开始 while(!que.empty()) { int cur = que.front(); // 当前顶点为队首元素 int i = head[cur]; // 与当前点(顶点)连接的边的序号 b[cur] = false; // 将当前顶点取消标记,应为后面我们可能还会添加进来(优化路径) while(i) // i 不为零,表示还有与cur相连的点 { int np = edge[i].to; if(dis[np] > dis[cur] + edge[i].w) { dis[np] = dis[cur] + edge[i].w; if(!b[np]) { que.push(np); b[np] = true; } } i = edge[i].next; } que.pop(); } for(int i = 1;i <= n;i++) cout << dis[i] << ' '; system("pause"); return 0; } void add_edge(int from, int to, int w) { //SPFA算法建立边比较固定,可以去b站找资源理解以下 num_edge++; edge[num_edge].next = head[from]; edge[num_edge].to = to; head[from] = num_edge; edge[num_edge].w = w; } ``` <p></p></div></div></div> ##### 例7 香甜的黄油(Sweet Butter) <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-77e249db880191593736b440758f23f884" aria-expanded="true"><div class="accordion-toggle"><span style="">题目描述:</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-77e249db880191593736b440758f23f884" class="collapse in collapse-content"><p></p> **【问题描述】** 农夫John发现做出全威斯康辛州最甜的黄油的方法:糖。把糖放在一片牧场上,他知道N(1<=N<=500)只奶牛会过来舔它,这样就能做出能卖好价钱的超甜黄油。当然,他将付出额外的费用在奶牛上。 农夫John很狡猾。像以前的巴甫洛夫,他知道他可以训练这些奶牛,让它们在听到铃声时去一个特定的牧场。他打算将糖放在那里然后下午发出铃声,以至他可以在晚上挤奶。 农夫John知道每只奶牛都在各自喜欢的牧场(一个牧场不一定只有一头牛)。给出各头牛在的牧场和牧场间的路线,找出使所有牛到达的路程和最短的牧场(他将把糖放在那)。 **【输入格式】** butter.in 第一行: 三个数:奶牛数N,牧场数P(2<=P<=800),牧场间道路数C(1<=C<=1450)。 第二行到第N+1行: 1到N头奶牛所在的牧场号。 第N+2行到第N+C+1行:每行有三个数:相连的牧场A、B,两牧场间距(1<=D<=255),当然,连接是双向的。 **【输出格式】** butter.out 一行 输出奶牛必须行走的最小的距离和 **【输入样例】** ```in 3 4 5 2 3 4 1 2 1 1 3 5 2 3 7 2 4 3 3 4 5 ``` **【输出样例】** ```out 8 //说明:放在4号牧场最优 ``` **【参考程序】** ```cpp #include <iostream> #include <queue> #include <cstring> #include <cmath> using namespace std; #define N 3005 const int INF = 0x7fffffff; int n,p,c; struct Edge{ // 边的一个结构体 int next; // 下一条边的编号 int to; // 这条边到达的点 int w; // 这条边的权重 }edge[N]; int num_edge = 0; // 边的序号 int head[N],dis[N],b[N]; // head[] 保存的是顶点 b[i] 存贮第 i 头牛所在的牧场号 bool exits[N]; queue<int> que; void add_edge(int from, int to, int w); // 添加边(创建连接表),参数分别是(边的起点,边的终点,边的权重) int main() { cin >> n >> p >> c; for(int i = 1; i <= n; i++) cin >> b[i]; //b[i] 存储每一头牛所在的牧场号 // 初始化边 for(int i = 1; i <= c; i++) { int from, to, w; cin >> from >> to >> w; add_edge(from, to, w); add_edge(to, from, w); } int minnum = INF; for(int i = 1; i <= p; i++) { memset(dis,0x7f,sizeof(dis)); dis[i] = 0; exits[i] = true; que.push(i); // 第 i 个牧场最为队首,入队 while(!que.empty()) { int cur = que.front(); // 获取队首元素 int i = head[cur]; // i 下一条边的编号,与当前顶点链接的编号 exits[cur] = false; // 将当前顶点取消标记,应为后面我们可能还会添加进来(优化路径) while(i) { int np = edge[i].to; // 当前边的终点 if(dis[np] > dis[cur] + edge[i].w) { dis[np] = dis[cur] + edge[i].w; if(!exits[np]) { que.push(np); exits[np] = true; } } i = edge[i].next; } que.pop(); } int total = 0; for(int j = 1; j <= n; j++) total += dis[b[j]]; if(total < minnum) minnum = total; } cout << minnum <<endl; system("pause"); return 0; } void add_edge(int from, int to, int w) { num_edge++; edge[num_edge].next = head[from]; edge[num_edge].to = to; edge[num_edge].w = w; head[from] = num_edge; } ``` <p></p></div></div></div> ### 5.最短路径算法对比比较(bellman-ford,dijkstra,spfa,floyd比较) <div id="article_content" class="article_content clearfix"> <link rel="stylesheet" href="https://csdnimg.cn/release/blogv2/dist/mdeditor/css/editerView/ck_htmledit_views-1a85854398.css"> <div id="content_views" class="htmledit_views"> <div class="table-box"><table border="1" cellpadding="1" cellspacing="1"><tbody><tr><td> </td><td>floyd (弗洛伊德算法)</td><td>Dijkstra(迪杰斯特拉算法)</td><td>bellman-ford(贝尔曼夫德算法)</td><td>spfa</td></tr><tr><td>空间复杂度 </td><td>O(N²)</td><td>O(M) </td><td>O(M)</td><td>O(M)</td></tr><tr><td>时间复杂度</td><td><span style="color:#4f4f4f;">O(N³)</span></td><td>O((m+n)logN)</td><td>O(MN)</td><td>最坏也是O(NM)</td></tr><tr><td>适用情况</td><td>稠密图和顶点关系密切</td><td><span style="color:#4f4f4f;">稠密图和顶点关系密切</span></td><td><span style="color:#4f4f4f;">稀疏图和边关系密切</span></td><td><span style="color:#4f4f4f;">稀疏图和边关系密切</span></td></tr><tr><td>负权</td><td>可以</td><td>不能</td><td>可以</td><td>可以</td></tr><tr><td>有负权边时可否处理</td><td>可以</td><td>不能</td><td>可以</td><td>可以</td></tr><tr><td>判断是否存在负权回路</td><td>不能</td><td>不能</td><td>可以</td><td>可以</td></tr></tbody></table></div> <p>其中N表示点数,M表示边数</p> <p>Floyd 算法虽然总体上时间复杂度较高,但可以处理带负权边的图(但不能有负权回路),并且均摊到每一点对上,在所有的算法中还是属于比较优秀的算法。另外,floyd算法较小的编码复杂度也是一大优势,所以,如果要求的是所有点对间的最短路径,或者如果数据范围较小,则floyd算法比较合适。</p> <p><span style="color:#4f4f4f;">Dijkstra</span>算法最大的弊端就是他无法处理带有负权边以及负权回路的图,但是<span style="color:#4f4f4f;">Dijkstra</span>算法具有良好的可扩展性,扩展后可以适应很多问题。另外用堆优化的<span style="color:#4f4f4f;">Dijkstra</span>算法的时间复杂度可以达到O(M log N)。当边有负权,甚至存在负权回路时,需要使用Bellman-ford 算法或者队列优化的Bellman-ford算法,因此我们选择最短路径法时,根据实际的需求和每一种算法的特性,选择合适的算法来使用。</p> </div><div><div></div></div> </div> # 二、输出最短路径 ### 1.单元最短路径的输出 Dijkstra、Bellman—Ford、SPFA 都是单源最短路径算法,它们的共同点是都有一个数组 pre[x] 用来记录从起点到 x 的最短路径中,x 的前驱结点是哪个。每次更新,就给 pre[x] 赋一个新值,结合上面的思想讲解,相信对于记录某点的前驱结点是不难理解的。那么怎么利用 pre[x] 数组输出最短路径方案呢? ##### 例8 最短路径输出问题 > 要求改写程序,用Dijkstra、Bellman—Ford或SPFA 算法输出最短路径的方案。 > > 使用一个小小递归过程就能解决这一问题。 > > ```cpp > void print(int x) > { > if(pre[a][x] == 0) return; // 起点的前驱我们已经设为0 > print(pre[a][x]); // 递归 > cout << " -> " << x; > } > > // 主程序中: > int main() > { > ....(进行Dijkstra、Bellman—Ford或SPFA 算法) > cout << s; // s 是起点 > print(e); // e是终点 > } > ``` ### 2.Floyed 算法输出最短路径 Floyed 算法输出路径也是采取记录前驱结点的方式。应为 floyed 是计算任意两个点的最短路径的算法,dis[i][j] 记录从 i 到 j 的最短路径值。故我们定义 pre[i][j] 为一个二维数组,记录从 i 到 j 的最短路径中, j 的前驱结点是哪一个。 ##### 例9 最短路径 Floyed 算法输出 要求改写Floyed的程序,模仿 Dijkstra 输出路径的方法用 floyed输出最短路径方案。 ```cpp #include <iostream> #include <cmath> #include <cstring> using namespace std; double dis[101][101]; int x[101], y[101]; int pre[101][101]; int n, i, j, k, m, a, b; void print(int x) { if(pre[a][x] == 0) return; // pre[a][a] == 0, 说明已经递归到起点 a print(pre[a][x]); cout << " -> " << x; } int main() { cin >> n; for(i = 1; i <= n; i++) cin >> x[i] >> y[i]; memset(dis,0x7f,sizeof(dis)); // 初始化数组 cin >> m; memset(pre,0,sizeof(pre)); // 初始化前驱数组 for(i = 1; i <= m; i++) { cin >> a >> b; dis[a][b] = dis[b][a] = sqrt(pow(x[a] - x[b],2) + pow(y[a] - y[b],2)); // a 与 b 相连,自然从 a 到 b 的最短路径 b 的前驱 是 a pre[a][b] = a; // 同理 pre[b][a] = b; } cin >> a >> b; // 起点 a 终点 b for(k = 1; k <= n; k++) for(i = 1; i <= n; i++) for(j = 1; j <= n; j++) if(i != j && i != k && j != k) // 这里需要额外注意 if(dis[i][j] > dis[i][k] + dis[k][j]) { dis[i][j] = dis[i][k] + dis[k][j]; // 从 i 到 j 的最短路径更新为 i->k->j,那么 i 到 j 最短路径 j 的前驱就肯定与 k 到 j 最短路径 j 的前驱相同。 pre[i][j] = pre[k][j]; } cout << a; // 先输出起点 print(b); // 后续遍历输出前驱结点 cout << endl; system("pause"); return 0; } ``` 最后再稍微提一提有向图求最短路径的方法:对有向图求最短路径上面的算法可以直接使用,只需要注意如果从 i 到 j 只有一条有向边, w[i][j] 赋值为这条边的权值,而将 w[j][i] 赋值为无穷大即可。 最后修改:2021 年 11 月 15 日 © 禁止转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏