【数据结构】图论算法_基础概念

博主： Fivk
发布时间：2021 年 07 月 31 日
1251 次浏览
暂无评论
2856字数
分类：数据结构

# 一、什么是图

很简单，用边连起来就叫做图，严格意义上将，图是一种数据结构，定义为：$graph=(V,E)$。V是一个非空有限集合，代表顶点（结点），E代表边的集合。

# 二、图的一些定义和概念

1. 有向图：图的边有方向，只能按箭头方向从一点到另一点。如图(a)就是一个有向图。
2. 无向图：图的边没有方向，可以双向。如图(b)就是一个无向图。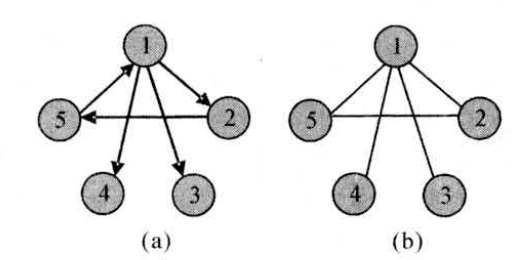![](https://blog.fivk.cn/usr/uploads/2021/07/3551238988.png)
3. 结点的度：无向图中与结点相连的边的数目，成为结点的度。
4. 结点的入度：在有向图中，以这个结点为终点的有向边的数目。
5. 结点的出度：在有向图中，以这个结点为起点的有向边的数目。
6. 权值：边的“费用”，可以形象地理解为边的长度。
7. 连通：如果图中结点U、V之间存在一条从U通过若干条边、点达到V的通路，则称U、V是连通的。
8. 回路：起点和终点相同的路径，称为回路，或“环”。
9. 完全图：一个n阶的完全无向图含有$n*(n-1)/2$条边；一个n阶完全有向图含有$n*(n-1)$条边。
10. 强连通分量：有向图中任意两点都连通的最大子图，如图中1-2-5构成一个强连通分量。特殊的，单个点也算一个强连通分量，所以图中有三个强连通分量：1-2-5，4，3。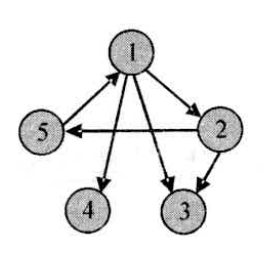

![](https://blog.fivk.cn/usr/uploads/2021/07/66593533.png)

稠密图：一个边数接近完全的图

洗漱图：一个边数远远少于完全图的图。

</div>

# 三、图的存储结构

### 1.二维数组邻接矩阵储存

定义 int G[101][101];

G[i][j]的值，表示从i到j的边权值，定义如下：

$$
G[i][j] =
        \begin{cases}
        1或权值,  & \text{当$v_i$与$v_j$之间有边或弧时，取值为1或权值} \\
        0或∞, & \text{当$v_i$与$v_j$之间无边或无弧时，取值为0或∞}
        \end{cases}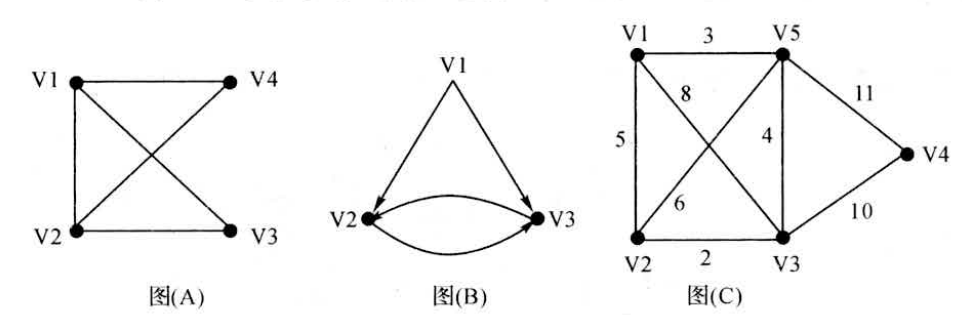

![](https://blog.fivk.cn/usr/uploads/2021/07/2922573728.png)

上图中3个图对应的邻接矩阵分别如下：

$$
G(A)=\left[
 \begin{matrix}
   0 & 1 & 1 & 1 \\
   1 & 0 & 1 & 1 \\
   1 & 1 & 0 & 0 \\
   1 & 1 & 0 & 0
  \end{matrix}
  \right]

$$
G(B)=\left[
 \begin{matrix}
   0 & 1 & 1 \\
   0 & 0 & 1 \\
   0 & 1 & 0 
  \end{matrix}
  \right]

$$
G(C)=\left[
 \begin{matrix}
   ∞ & 5 & 8 & ∞ & 3 \\
   5 & ∞ & 2 & ∞ & 6 \\
   8 & 2 & ∞ & 10 & 4 \\
   ∞ & ∞ & 10 & ∞ & 11 \\
   3 & 6 & 4 & 11 & ∞  \\
  \end{matrix}
  \right]

下面是建立图的邻接矩阵的参考程序：

```cpp
#include <iostream>
using namespace std;

int i,j,k,e,n;
double G[101][101];
double w;

int main()
{
    int i,j;
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            G[i][j]=)x7fffffff;

//初始化，对于不带权重的图，G[i][j]=0，表示没有边连通。这里用0x7fffffff代替无穷大

cin>>e;

for(k=1;k<=e;k++)
    {
        cin>>i>>j>>w;   //读入两个顶点序号及权值
        G[i][j]=w;      //对于不带权值的图 G[i][j]=1;
        G[j][i]=w;      //无向图的对称性，如果是有向图则不要这一句
    }

//省略

system("pause");
    return 0;
}
```

建立相邻矩阵时，有两个小技巧：

初始化数组大可不必使用两重for循环。

1. 如果时int数组，采用`memset(G,0x7f,sizeof(G))`可全部初始化为一个很大的树（略小于0x7fffffff）;使用`memset(G,0,sizeof(G))`，全部清为0；使用`memset(G,0,sizeof(G))`，全部初始化为一个很小的数。
2. 如果是double数组，采用`memset(G,127,sizeof(G))`，可全部初始化为一个很大的数$1.38*10^{306}$；使用`memset(G,0,sizeof(G))`，全部清为0。

</div>

### 2.数组模拟邻接表存储

图的邻接表存储发，又叫链式存储发。本来是要采用链表实现的，但大多数情况下只要用数组模拟即可。

以下是数组模拟邻接表存储的参考程序：

```cpp
#include <iostream>
using namespace std;

const int maxn=1001,maxm=100001;
struct Edge
{
    int next;   //下一边的编号
    int to;     //这边到达的店
    int dis;    //这条边的长度
}edge[maxm];

int head[maxn],num_edge,n,u,m,v,d;

void add_edge(int from,int to,int dis)
            //加入一条从from到to距离为dis的单位边
{
    edge[++num_edge].next=head[from];
    edge[num_edge].to=to;
    edge[num_dege].dis=dis;
    head[from]=num_edge;
}

int main()
{
    num_dege=0;
    scanf("%d %d",&n,&m);   //读入点数和边数
    for(int i=1;i<=m;i++)
    {
        scanf("%d %d %d",&u,&v,&d); //u、v之间有一条长为d的边
        add_edge(u,v,d);
    }

for(int i=head[1];i!=0;i=edge[i].next)      //遍历从1开始的所有边
    {
        //……
    }
  
    //……

return 0;
}
```

两种方各有用武之地，需按具体情况，具体选用。

最后修改：2021 年 09 月 12 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

【数据结构】图论算法_基础概念

Fivk • 2021 年 07 月 31 日

# 一、什么是图

很简单，用边连起来就叫做图，严格意义上将，图是一种数据结构，定义为：$graph=(V,E)$。V是一个非空有限集合，代表顶点（结点），E代表边的集合。

# 二、图的一些定义和概念

![](https://blog.fivk.cn/usr/uploads/2021/07/66593533.png)

稠密图：一个边数接近完全的图

洗漱图：一个边数远远少于完全图的图。

</div>

# 三、图的存储结构

### 1.二维数组邻接矩阵储存

定义 int G[101][101];

G[i][j]的值，表示从i到j的边权值，定义如下：

![](https://blog.fivk.cn/usr/uploads/2021/07/2922573728.png)

上图中3个图对应的邻接矩阵分别如下：

$$
G(A)=\left[
 \begin{matrix}
   0 & 1 & 1 & 1 \\
   1 & 0 & 1 & 1 \\
   1 & 1 & 0 & 0 \\
   1 & 1 & 0 & 0
  \end{matrix}
  \right]

$$
G(B)=\left[
 \begin{matrix}
   0 & 1 & 1 \\
   0 & 0 & 1 \\
   0 & 1 & 0 
  \end{matrix}
  \right]

$$
G(C)=\left[
 \begin{matrix}
   ∞ & 5 & 8 & ∞ & 3 \\
   5 & ∞ & 2 & ∞ & 6 \\
   8 & 2 & ∞ & 10 & 4 \\
   ∞ & ∞ & 10 & ∞ & 11 \\
   3 & 6 & 4 & 11 & ∞  \\
  \end{matrix}
  \right]

下面是建立图的邻接矩阵的参考程序：

```cpp
#include <iostream>
using namespace std;

int i,j,k,e,n;
double G[101][101];
double w;

int main()
{
    int i,j;
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            G[i][j]=)x7fffffff;

//初始化，对于不带权重的图，G[i][j]=0，表示没有边连通。这里用0x7fffffff代替无穷大

cin>>e;

//省略

system("pause");
    return 0;
}
```

建立相邻矩阵时，有两个小技巧：

初始化数组大可不必使用两重for循环。

</div>

### 2.数组模拟邻接表存储

图的邻接表存储发，又叫链式存储发。本来是要采用链表实现的，但大多数情况下只要用数组模拟即可。

以下是数组模拟邻接表存储的参考程序：

```cpp
#include <iostream>
using namespace std;

const int maxn=1001,maxm=100001;
struct Edge
{
    int next;   //下一边的编号
    int to;     //这边到达的店
    int dis;    //这条边的长度
}edge[maxm];

int head[maxn],num_edge,n,u,m,v,d;

for(int i=head[1];i!=0;i=edge[i].next)      //遍历从1开始的所有边
    {
        //……
    }
  
    //……

return 0;
}
```

两种方各有用武之地，需按具体情况，具体选用。

【数据结构】图论算法_基础概念

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

【Fivk】文章归档

回忆刚入天柱二中的我

【C】求小数的某一位

【动态规划】完全背包

[函数快查] fread -- 从文件中读取数据

【Tool】EasyExcel

【开发技巧】利用CollUtil一行代码将对象中的属性提取转化为List

【数据结构】图论算法_基础概念

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【数据结构】图论算法_基础概念

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款