【数据结构】课前测试填空题1

我打算做一个课前测试填空题题集，感觉数据结构有一点悬。每次我保存题目，后面来完成，每次都可以更新一点。

</div>

# 题1

下列代码的功能是使用Prim算法求出无向图的最小生成树权值总和，请补全。

给出的图用邻接矩阵存储。若两顶点之间没有直接路径，则对应权值为 `INF`，且题目保证 INF 值足够大；若找不到距离最短的顶点或者无法求出权值总和，则返回 `ERROR`。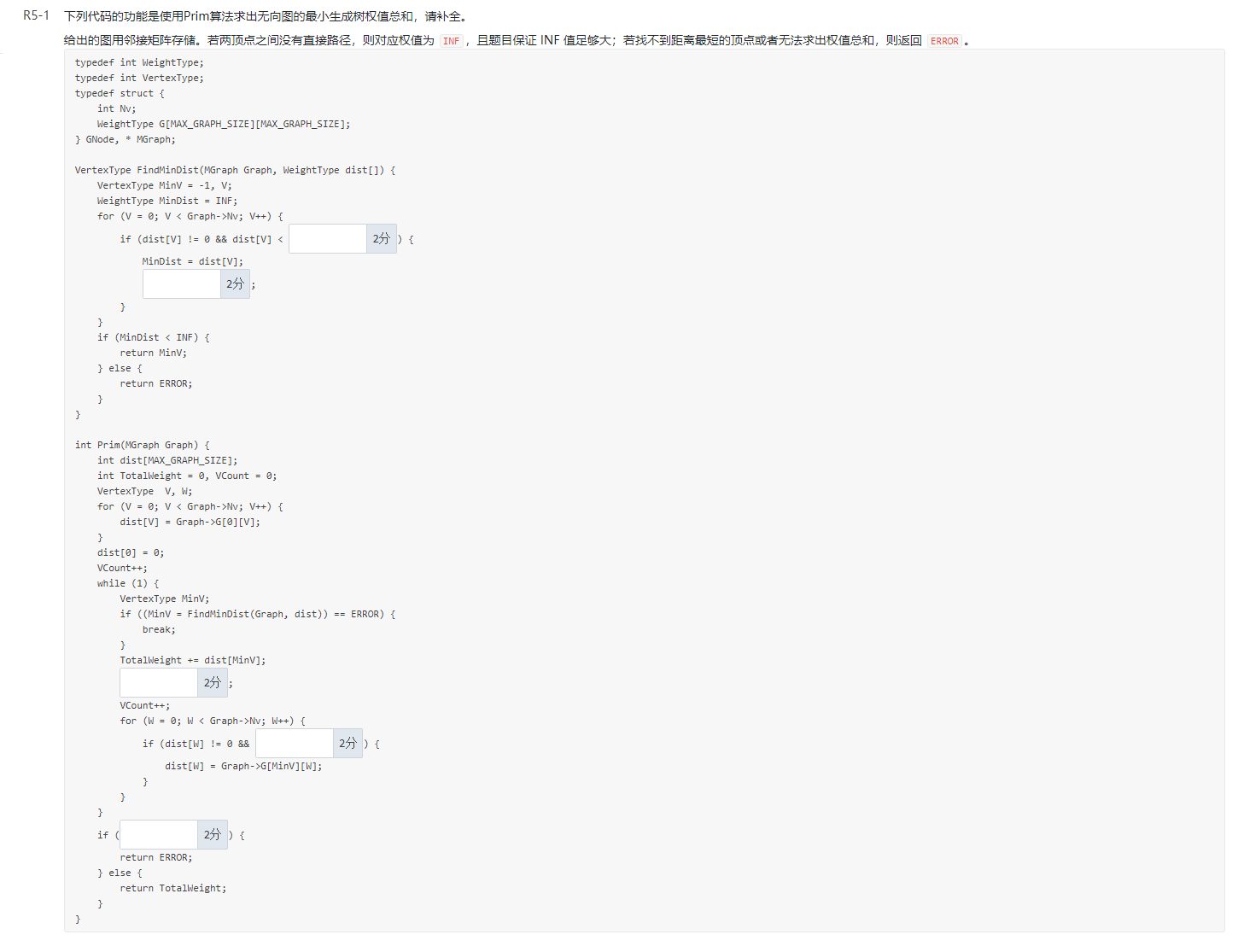

![](https://blog.fivk.cn/usr/uploads/2021/11/948063931.png)

```c
typedef int WeightType;
typedef int VertexType;
typedef struct {
    int Nv;
    WeightType G[MAX_GRAPH_SIZE][MAX_GRAPH_SIZE];
} GNode, * MGraph;

VertexType FindMinDist(MGraph Graph, WeightType dist[]) {
    VertexType MinV = -1, V;
    WeightType MinDist = INF;
    for (V = 0; V < Graph->Nv; V++) {
        if (dist[V] != 0 && dist[V] < ##填空1##) {
            MinDist = dist[V];
            ##填空2##;
        }
    }
    if (MinDist < INF) {
        return MinV;
    }
    else {
        return ERROR;
    }
}

int Prim(MGraph Graph) {
    int dist[MAX_GRAPH_SIZE];
    int TotalWeight = 0, VCount = 0;
    VertexType  V, W;
    for (V = 0; V < Graph->Nv; V++) {
        dist[V] = Graph -> G[0][V];
    }
    dist[0] = 0;
    VCount++;
    while (1) {
        VertexType MinV;
        if ((MinV = FindMinDist(Graph, dist)) == ERROR) {
            break;
        }
        TotalWeight += dist[MinV];
        ##填空3##;
        VCount++;
        for (W = 0; W < Graph->Nv; W++) {
            if (dist[W] != 0 && ##填空4##) { 
                dist[W] = Graph->G[MinV][W];
            }
        }
    }
    if (##填空5##) {
        return ERROR;
    }
    else {
        return TotalWeight;
    }
}
```

# 我的程序

<div class="hideContent">此处内容需要评论回复后（审核通过）方可阅读。</div>

最后修改：2021 年 11 月 19 日