Loading... ### 1.简介 线段树可以做很多事情,树状数组能做的线段树都能够实现。原理上线段树是一个非常简单的数据结构,但是在代码上比树状数组麻烦。线段树和树状数组都是维护一个序列,但是线段树可以进行的操作有很多,基本没有什么限制,不仅仅可以做单点,还可以做比如“区间的最大值”、“区间减法”、“染色”、“区间面积”、“长度”、“最大连续和”等等。 ### 2.原理 线段树是一个完全二叉树的数据结构,对于每一个节点: ```cpp struct node { int l, r; int sum; }; ``` 根节点存放的是所有数的总和。 比如一个`[1, 7]`这一个区间,根节点存放这七个数的总和`28`,每一个区间,如果长度不是`1`的话,就会尽量平均分成两份,比如这里我们分为`[1, 4]`,和`[5, 7]`。 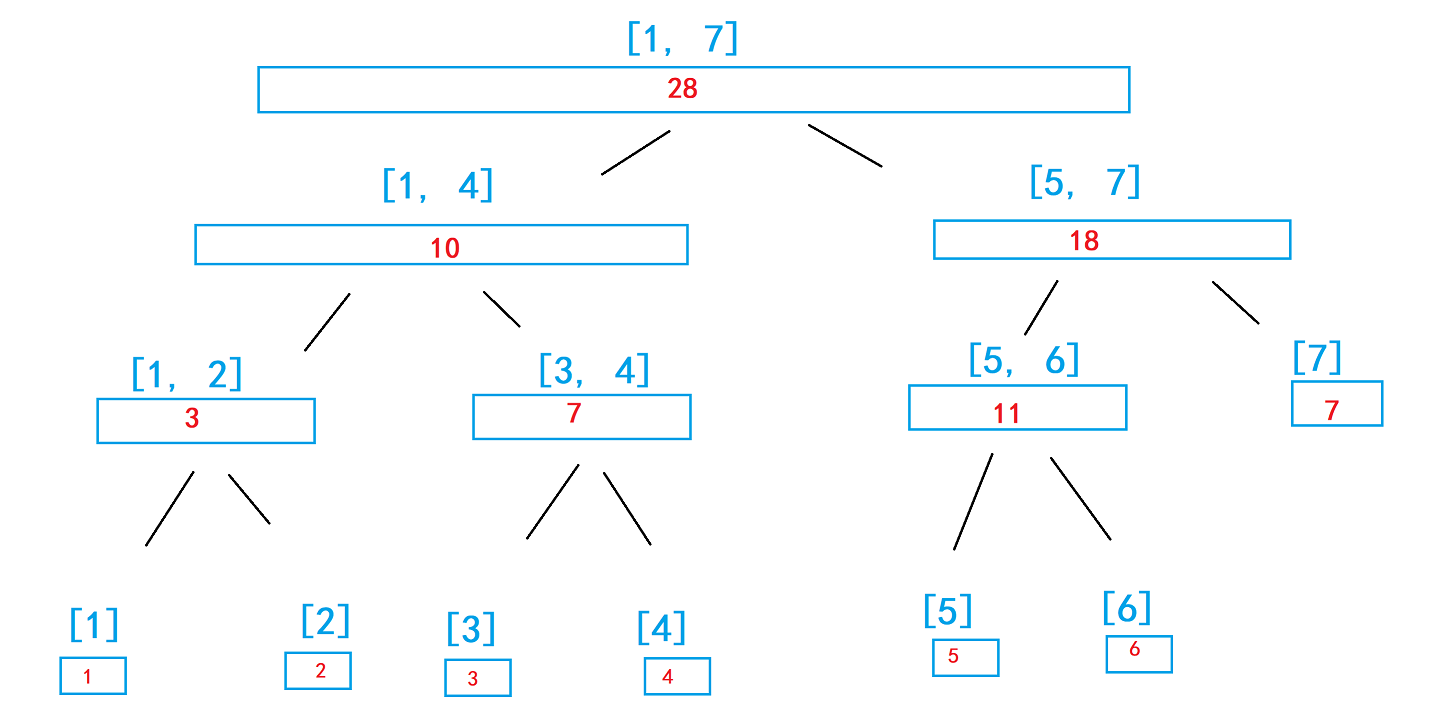 > 这个结构就相对简单了,每次对半开即可。 <div class="tip inlineBlock success"> 对于区间划分为两段的方法: `[L, R]`划分为`[L, Mid]`与`[Mid + 1, R]` 其中$Mid = \lfloor \frac{L+R}{2} \rfloor$ </div> ### 3.存储方式 和堆类似,使用数组进行存储,且数组最大长度不会超过`4N`。  ### 4.操作 #### 单点修改O(logn) > 作用:修改这段区间的某一个值,并更新线段树。 单点修改是一个递归的过程,只需要修改信息需要变化的节点(与修改节点相关的节点)即可,比如我们修改上图的`5`,我们只需要修改`[1, 7]`、`[5, 7]`、`[5, 6]`、`[5]`这4个节点即可。 #### 区间查询O(logn) > 作用:查询某一个区间的总和是多少。 区间查询也是一个递归的过程,比如求`2 ~ 5`这一段的区间是多少,我们是不断往下递归,直到完全包含这段区间位置。 #### 四个函数 1. pushup:用子节点信息更新当前节点信息 2. build:在一段区间上初始化线段树 3. modify:修改操作 4. query:查询操作 ### 5案例:动态求连续区间和 给定 `n` 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 `[a,b]` 的连续和。 #### 输入格式 第一行包含两个整数 `n` 和 `m`,分别表示数的个数和操作次数。 第二行包含 `n` 个整数,表示完整数列。 接下来 `m` 行,每行包含三个整数 `k, a, b` (`k = 0`,表示求子数列`[a, b]`的和;`k = 1`,表示第 `a` 个数加 `b`)。 数列从 `1` 开始计数。 #### 输出格式 输出若干行数字,表示 `k=0` 时,对应的子数列 `[a, b]` 的连续和。 #### 数据范围 `1≤n≤100000,` `1≤m≤100000,` `1≤a≤b≤n,` 数据保证在任何时候,数列中所有元素之和均在 int 范围内。 #### 输入样例: ```in 10 5 1 2 3 4 5 6 7 8 9 10 1 1 5 0 1 3 0 4 8 1 7 5 0 4 8 ``` #### 输出样例: ```out 11 30 35 ``` ### 线段树模板 ```cpp #include <iostream> using namespace std; const int N = 1e5 + 10; int n, m; int w[N]; // 权值 struct Node { int l, r; int sum; }tr[N * 4]; void push_up(int u) { tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum; } // u 是根节点 void build(int u, int l, int r) { if (l == r) tr[u] = {l, r, w[r]}; else { // 赋左右边界初值 tr[u] = {l, r}; // 左右孩子递归 int mid = l + r >> 1; build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r); // 更新 push_up(u); } } int query(int u, int l, int r) { if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum; int sum = 0; // 判断是否有交集 int mid = tr[u].l + tr[u].r >> 1; if (mid >= l) sum = query(u << 1, l, r); if (mid < r) sum += query(u << 1 | 1, l, r); return sum; } void modify(int u, int x, int v) { if (tr[u].l == tr[u].r) tr[u].sum += v; else { int mid = tr[u].l + tr[u].r >> 1; if (x <= mid) modify(u << 1, x, v); else modify(u << 1 | 1, x, v); push_up(u); } } int main() { scanf("%d %d", &n, &m); for (int i = 1; i <= n; i ++) scanf("%d", &w[i]); build(1, 1, n); int k, a, b; while (m --) { scanf("%d %d %d", &k, &a, &b); if (k == 0) printf("%d\n", query(1, a, b)); else modify(1, a, b); } return 0; } ``` 最后修改:2022 年 03 月 21 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏
1 条评论
学习了,值得收藏的知识点