【算法基础】树状数组 - 动态求连续区间和

Fivk

2022 年 03 月 04 日

1039 次浏览

暂无评论

346字数

算法基础

![](https://blog.fivk.cn/usr/uploads/2022/03/3507239177.png)

### 1.功能

1. 让某个位置上的数加上一个数 $O(log⁡n)$
2. 求某一个前缀和 $O(logn)$

### 2.操作

1. `lowbit(x)`:返回`x`的最后一位`1`
2. `add(x,v)`:在`x`位置加上`v`，并将后面相关联的位置也加上`v`
3. `query(x)`:询问x的前缀和
4. `c[x]`表示的区间和是`(x−lowbit(x),x]`

#### add(x,k)操作

需要让后面所有包含元素$x$区间和都增加$k$

```cpp
for (int i = x; i <= n; i += lowbit(i)) {
   c[i] += k;
}
```

#### query(x)操作

需要累加$x$前面全部的元素，每个$i$包含了$(i−lowbit(i),i]$的数

```cpp
for (int i = x; i; i -= lowbit(i)) {
    sum += c[i];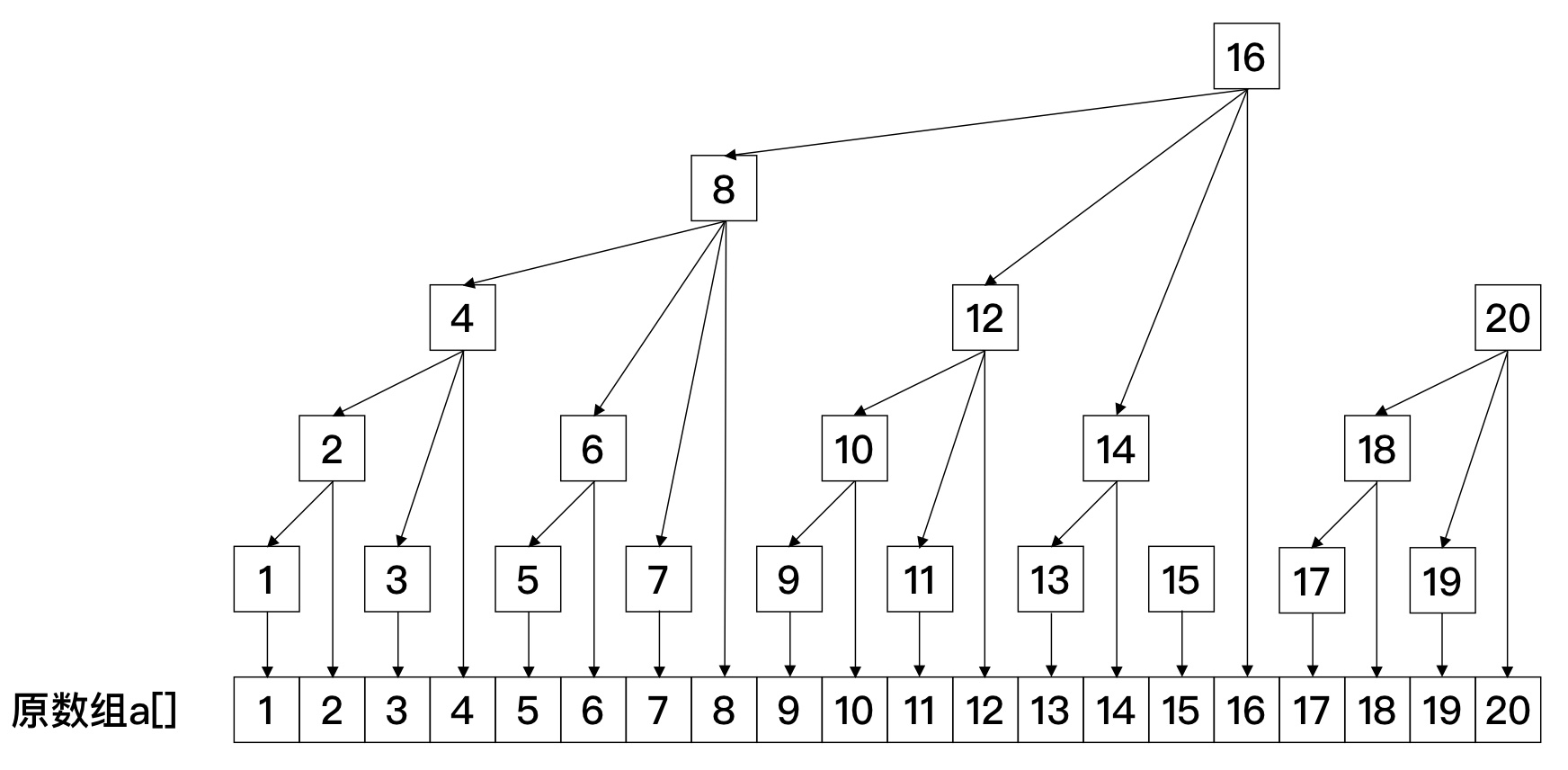
}
```

![](https://blog.fivk.cn/usr/uploads/2022/03/2124169275.jpg)

### 案例：动态求连续区间和

给定 `n` 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 `[a,b]` 的连续和。

#### 输入格式

第一行包含两个整数 `n` 和 `m`，分别表示数的个数和操作次数。

第二行包含 `n` 个整数，表示完整数列。

接下来 `m` 行，每行包含三个整数 `k, a, b` （`k = 0`，表示求子数列`[a, b]`的和；`k = 1`，表示第 `a` 个数加 `b`）。

数列从 `1` 开始计数。

#### 输出格式

输出若干行数字，表示 `k=0` 时，对应的子数列 `[a, b]` 的连续和。

#### 数据范围

`1≤n≤100000,`
`1≤m≤100000,`
`1≤a≤b≤n,`
数据保证在任何时候，数列中所有元素之和均在 int 范围内。

#### 输入样例：

```in
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
```

#### 输出样例：

```out
11
30
35
```

### 树状数组模板

```cpp
#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int n, m;
int c[N];

//lowbit返回二进制第一个非零的1
int lowbit(int x) {
    return x & -x;
}
//在第x个位置上，加上k
void add(int x, int k) {
    for (int i = x; i <= n; i += lowbit(i)) c[i] += k;
}
//返回x的前缀和
int query(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += c[i];
    return res;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        int x;
        scanf("%d", &x);
        add(i, x);
    }
    while (m--) {
        int k, a, b;
        scanf("%d %d %d", &k ,&a, &b);
        if (k) add(a, b);
        else printf("%d\n", query(b) - query(a - 1));
    }
    return 0;
}
```

最后修改：2022 年 03 月 05 日