Loading... <div class="tip inlineBlock info"> 检验各因素之间有没有关联程度。 般情况下. - `KMO`值应大于等于`0.6` - `Sig`值应小于等于`0.05` </div> 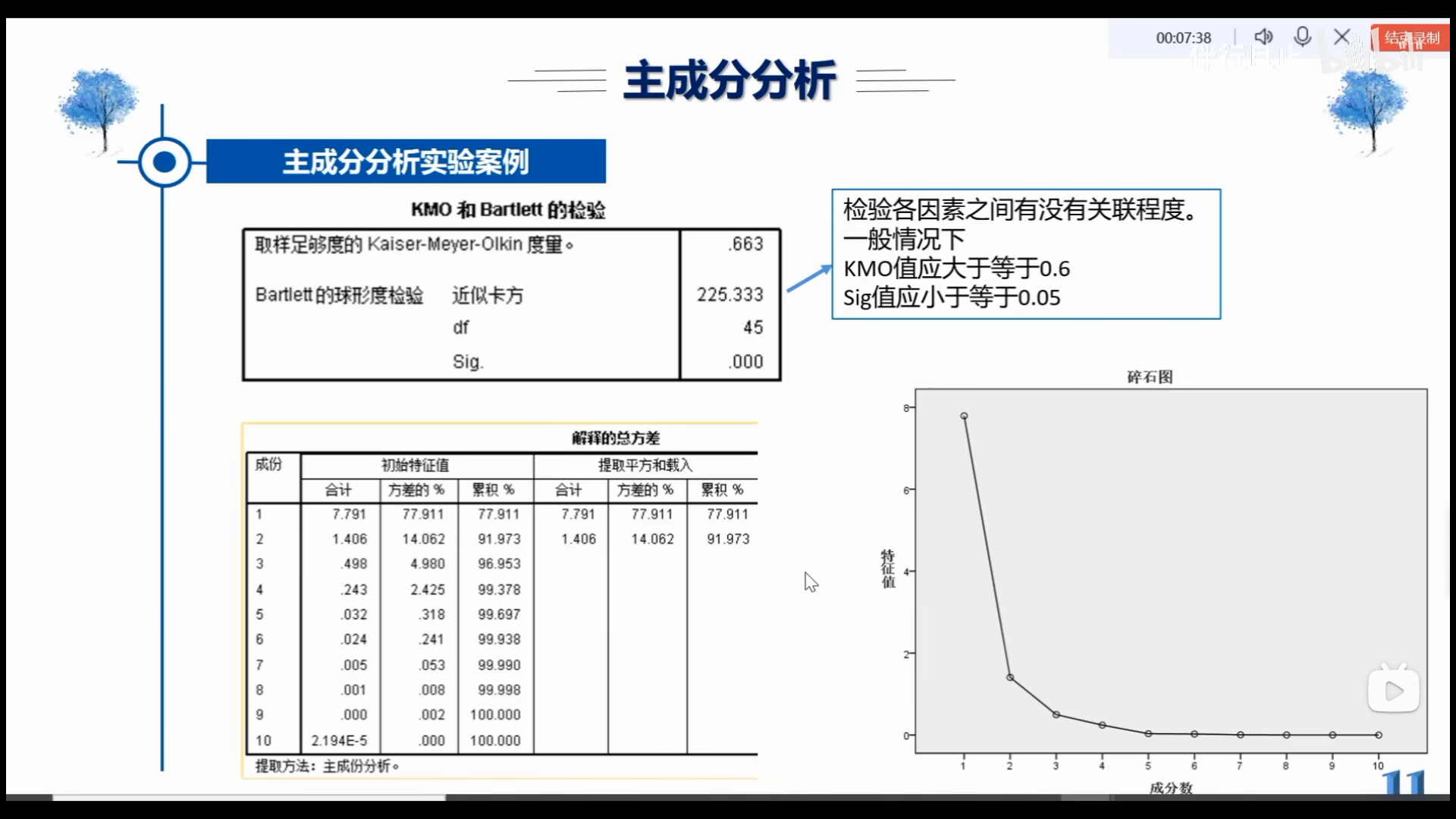 # 一、填空题 1.第j个主成分与原始变量$x_i$的相关系数称为 **#填空** <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-dd4db9583b9e5d5d8b15318489b2467699" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-dd4db9583b9e5d5d8b15318489b2467699" class="collapse collapse-content"><p></p> 因子负荷量 <p></p></div></div></div> 2.各主成分的协方差矩阵是 **#填空** <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-d7f83bff49b7752f9ad60ae8c2c1ed3c91" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-d7f83bff49b7752f9ad60ae8c2c1ed3c91" class="collapse collapse-content"><p></p> 对角阵 <p></p></div></div></div> 3.在主成分分析中,因子负荷$a_{ij}$的统计意义是 **#填空** <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-2002b7d8ed36a758123f98764bed3f316" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-2002b7d8ed36a758123f98764bed3f316" class="collapse collapse-content"><p></p> 第`i`个主成分与原始变量`j`的相关系数。 <p></p></div></div></div> 4.因子分析中,因子载荷系数$a_{ij}$的统计意义是 **#填空** <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-5221e095d8d8cd04295c5c2090bd667a93" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-5221e095d8d8cd04295c5c2090bd667a93" class="collapse collapse-content"><p></p> 是$X_i$与$F_j$的协方差和相关系数。 <p></p></div></div></div> 5.因子分析中$g_i^2$是指 **#填空1**,$H_i^2$表示 **#填空2**。 <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-c0c127b334a3020f0890a97261610ba473" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-c0c127b334a3020f0890a97261610ba473" class="collapse collapse-content"><p></p> 填空1:方差贡献率 填空2:共同度 <p></p></div></div></div> 6.公共因子方差与特殊因子方差之和为 `1` 7.样本主成分的总方差为 `1` 8.标准化数据的协方差矩阵正好是原数据的 **#填空** <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-ce3c7af10a81542c23be8f0a99895d98100" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-ce3c7af10a81542c23be8f0a99895d98100" class="collapse collapse-content"><p></p> 相关矩阵 <p></p></div></div></div> # 二、简答题 ### 1. 在数据处理时,为什么通常要进行标准化处理? <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-30c609faed8fc8f7c097779c9d20fbdd34" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-30c609faed8fc8f7c097779c9d20fbdd34" class="collapse collapse-content"><p></p> 对数据进行标准化处理主要为了消除变量的量纲以及量纲差别较大时所带来的影响 <p></p></div></div></div> ### 2. 欧氏距离与马氏距离的优缺点是什么? <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-e0f18f41d8d0cab711aa5fa1749a777970" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-e0f18f41d8d0cab711aa5fa1749a777970" class="collapse collapse-content"><p></p> 欧氏距离: - 优点:是点与点计算的常用方法 - 缺点:其缺点是坐标的各维度对计算距离的贡献是同等的 马氏距离: - 优点:弥补了欧氏距离在统计问题上的缺陷,马氏距离的计算中会将各指标变量转化为无量纲的数值 - 缺点: <p></p></div></div></div> ### 3. 聚类分析的基本思想和功能是什么? <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-12158dd75a8b4100a215e00ddf5c8f6544" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-12158dd75a8b4100a215e00ddf5c8f6544" class="collapse collapse-content"><p></p> 聚类分析首先假定所研究的样品或指标(变量)之间存在不同程度的相似性(亲疏关系),然后对于给定的一批有多个观测指标的样品,可以根据一些能够度量样品或指标之间相似程度的统计量作为划分类型的依据,最终把相似程度接近的样品(指标)聚合为同一类。聚类分析的目的就是把研究对象根据相似程度进行归类,使同类中对象的相似最大化,而类与类之间的差异性最大化。 <p></p></div></div></div> ### 4. 试述系统聚类法的原理和具体步骤。 <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-1f0635471b9a73c17f2bfbb8cc33039f69" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-1f0635471b9a73c17f2bfbb8cc33039f69" class="collapse collapse-content"><p></p> 系统聚类的原理是根据样品(或指标变量)间的距离(或相似性)进行类的合并,首先将各样品或(变量)当作一类,然后每次将距离最近(或相似度最高)的两类(或变量)聚合成一类,如此重复进行下去,直至每个样品(或变量)最终被聚成一个大类。 系统聚类的具体步骤如下: 1. 将每个样品(或变量)独自作为一类,如此构造$n$个类; 2. 计算$n$个类两两之间的距离${d_{ij}}$; 3. 合并距离最近的两类为一新类,并重新计算类与类之间的距离; 4. 重复步骤3; 5. 直至最后将所有样品(或变量)全被聚一个类。 <p></p></div></div></div> ### 5.试述 K-均值聚类的方法原理。 <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-959e62141df9cd25f2b6649138572b8b58" aria-expanded="true"><div class="accordion-toggle"><span style="">答案</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-959e62141df9cd25f2b6649138572b8b58" class="collapse collapse-content"><p></p> K-均值聚类方法的思想是把每个样品聚集到其最近质心(均值)的类中,它是一种迭代求解的聚类分析算法。 1. 其步骤是:首先从数据集中随机选取k个点作为初始聚类中心 2. 然后计算各个样本到聚类中心的距离,并把样本归到离它最近的那个聚类中心所在的类 3. 最后计算新形成的每一个类所包含对象的平均值作为新的聚类中心。 4. 重复前面的操作,直至相邻两次的聚类中心没有任何变化,说明样本调整结束。 <p></p></div></div></div> <div class="tip inlineBlock share"> 来源教材 </div> 最后修改:2022 年 07 月 06 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 3 如果觉得我的文章对你有用,请随意赞赏