【动态规划】01背包

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

#### 输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

#### 输出格式

输出一个整数，表示最大价值。

#### 数据范围

0<N,V≤1000
0<vi,wi≤1000

#### 输入样例

```
4 5
1 2
2 4
3 4
4 5
```

#### 输出样例：

```
8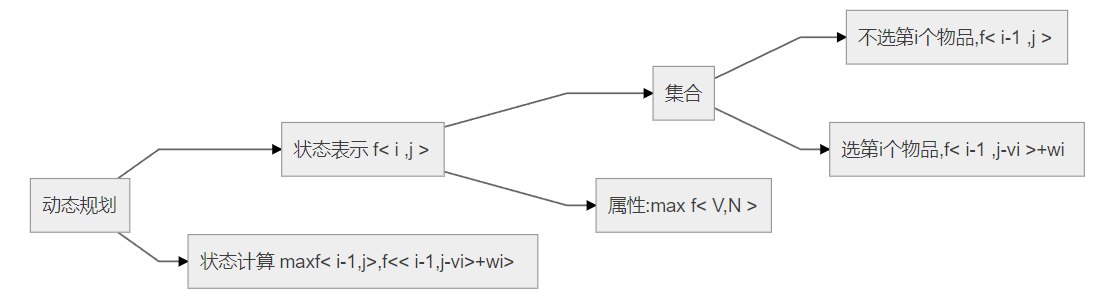
```

![](https://blog.fivk.cn/usr/uploads/2022/01/1671317345.png)

**优化一般就是优化状态转移方程**

### 01背包

**特点:** 每个物品仅能使用一次
**重要变量&公式解释**
`f[i][j]`:表示所有选法集合中,只从前`i`个物品中选,并且总体积$\le j$的选法的集合,它的值是这个集合中每一个选法的最大值.

### 状态转移方程

`f[i][j] = max(f[i-1][j], f[i-1][j-v[i]]+w[i])`

`f[i-1][j]`:不选第i个物品的集合中的最大值

`f[i-1][j-v[i]]+w[i]`:选第`i`个物品的集合,但是直接求不容易求所在集合的属性,这里迂回打击一下,先将第`i`个物品的体积减去,求剩下集合中选法的最大值.

### 问题

集合如何划分

- 一般原则:不重不漏,不重不一定都要满足(一般求个数时要满足)
- 如何将现有的集合划分为更小的子集,使得所有子集都可以计算出来.

### 无优化版

```cpp
#include <iostream>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i++) {
        for(int j = 0; j <= m; j++) {
            f[i][j] = f[i-1][j];
            if(j>=v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);
        }
    }

cout << f[n][m] << endl;
 return 0;  
}
```

### 有优化版

1. f[i] 仅用到了f[i-1]层,
2. j与j-v[i] 均小于j
3. 若用到上一层的状态时,从大到小枚举, 反之从小到大哦

```cpp
#include <iostream>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i++) 
        for(int j = m; j >= v[i]; j--) 
            f[j] = max(f[j], f[j-v[i]]+w[i]);
    cout << f[m] << endl;
 return 0;  
}
```

最后修改：2022 年 01 月 07 日