Loading... ### 基本思考框架 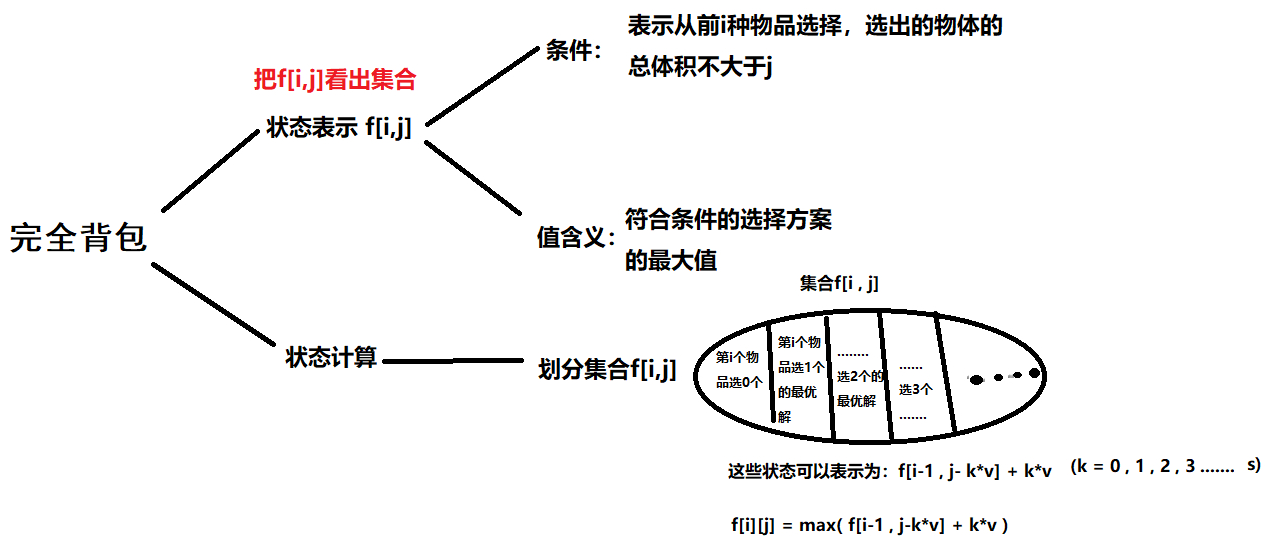 废话少说,看看什么是完全背包: ### 完全背包 有 `N` 种物品和一个容量是 `V` 的背包,每种物品都有无限件可用。 第 `i` 种物品的体积是 `vi`,价值是 `wi`。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值。 #### 输入格式 第一行两个整数`N`,`V`,用空格隔开,分别表示物品种数和背包容积。 接下来有 `N` 行,每行两个整数 `vi`,`wi`,用空格隔开,分别表示第 `i` 种物品的体积和价值。 #### 输出格式 输出一个整数,表示最大价值。 #### 数据范围 0<N,V≤1000 0<vi,wi≤1000 #### 输入样例 ``` 4 5 1 2 2 4 3 4 4 5 ``` #### 输出样例: ``` 10 ``` 完全背包的每个物品可以用无限次,其他条件与01背包一致。 ### 分析 <div class='album_block'> [album type="photos"] 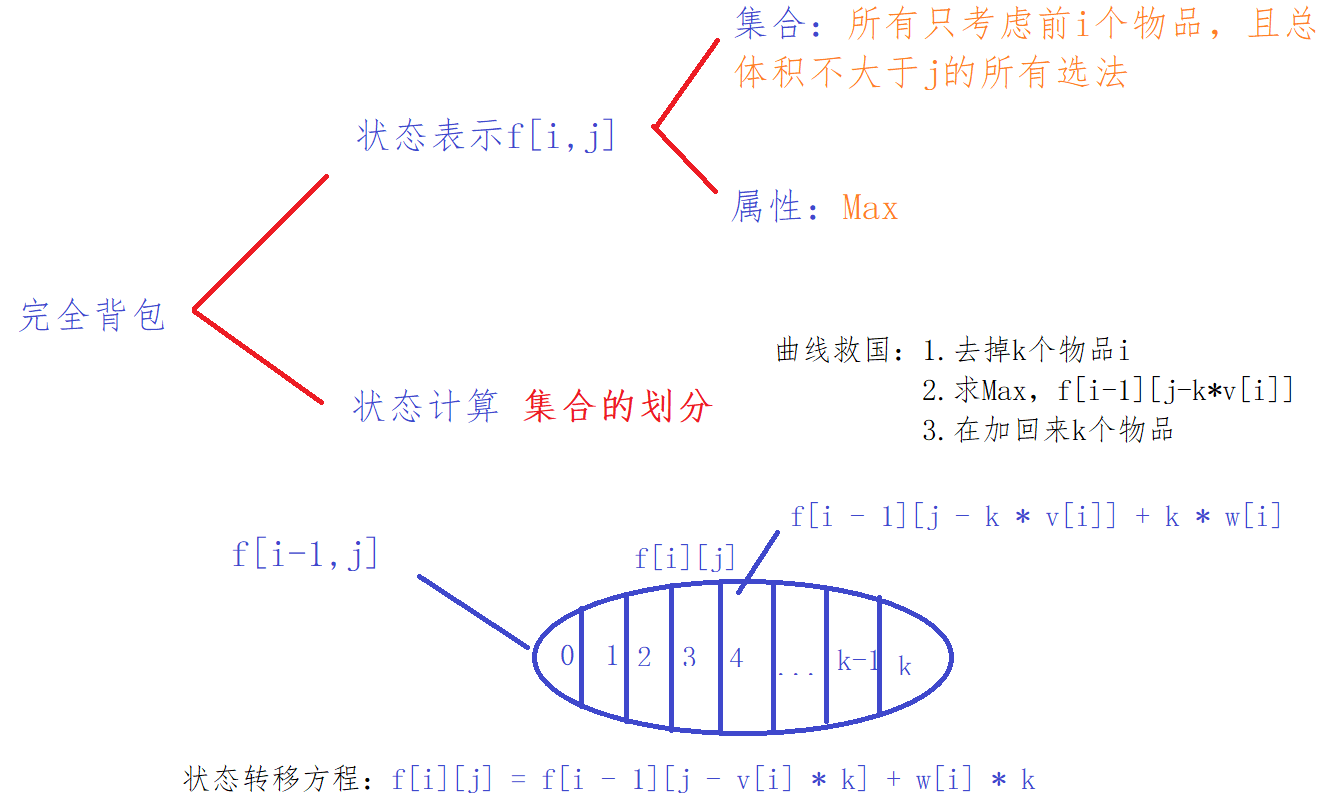 [/album] </div> ```cpp #include<iostream> using namespace std; const int N = 1010; int f[N][N]; int v[N],w[N]; int main() { int n,m; cin>>n>>m; for(int i = 1 ; i <= n ;i ++) { cin>>v[i]>>w[i]; } for(int i = 1 ; i<=n ;i++) for(int j = 0 ; j<=m ;j++) for(int k = 0 ; k*v[i]<=j ; k++) f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]); cout<<f[n][m]<<endl; } ``` ### 优化 我们观察`f[i][j] = f[i - 1][j - v[i] * k] + w[i] * k`,对k展开,`v[i]`用`v`表示,`w[i]`用`w`表示: $$ f[i][j] = Max(f[i-1][j], f[i-1][j-v]+w, f[i-1][j-2v]+2w,f[i-1][j-3v]+3w,...) $$ $$ f[i][j-v] = Max(f[i-1][j-v],f[i-1][j-2v]+w,f[i-1][j-3v]+2w,...) $$ 观察可以发现,下面这个规律:  我们最后得到**状态转移方程:** `f[i][j] = max(f[i][j], f[i][j-v[i]] + w)` 有了上面的关系,那么其实k循环可以不要了,核心代码优化成这样: ```cpp for(int i = 1 ; i <=n ;i++) for(int j = 0 ; j <=m ;j++) { f[i][j] = f[i-1][j]; if(j-v[i]>=0) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]); } ``` 这个代码和01背包的非优化写法很像啊!!!我们对比一下,下面是01背包的核心代码 ```cpp for(int i = 1 ; i <= n ; i++) for(int j = 0 ; j <= m ; j ++) { f[i][j] = f[i-1][j]; if(j-v[i]>=0) f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]); } ``` 两个代码其实只有一句不同(注意下标) `f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);`//01背包 `f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);`//完全背包问题 因为和01背包代码很相像,我们很容易想到进一步优化。核心代码可以改成下面这样 ```cpp for(int i = 1 ; i<=n ;i++) for(int j = v[i] ; j<=m ;j++)//注意了,这里的j是从小到大枚举,和01背包不一样 { f[j] = max(f[j],f[j-v[i]]+w[i]); } ``` 综上所述,完全背包的最终写法如下: ```cpp #include<iostream> using namespace std; const int N = 1010; int f[N]; int v[N],w[N]; int main() { int n,m; cin>>n>>m; for(int i = 1 ; i <= n ;i ++) { cin>>v[i]>>w[i]; } for(int i = 1 ; i<=n ;i++) for(int j = v[i] ; j<=m ;j++) { f[j] = max(f[j],f[j-v[i]]+w[i]); } cout<<f[m]<<endl; } ``` 最后修改:2022 年 01 月 07 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 2 如果觉得我的文章对你有用,请随意赞赏
2 条评论
您好~我是腾讯云+社区的运营,关注了您在分享的技术文章,觉得内容很棒,我们诚挚邀请您加入腾讯云自媒体分享计划。完整福利和申请地址请见:https://cloud.tencent.com/developer/support-plan
作者申请此计划后将作者的文章进行搬迁同步到社区的专栏下,你只需要简单填写一下表单申请即可,我们会给作者提供包括流量、云服务器等,另外还有些周边礼物。 我们诚挚的邀请您并期待您的加入~
非人类