【动态规划】多重背包

博主： Fivk
发布时间：2022 年 01 月 06 日
1040 次浏览
3186字数
分类：题目典例

# 前言

多重背包暴力算法其实和完全背包暴力算法差不多，但优化方面相对复杂了很多，多重背包不能像完全背包一样推导出状态转移方程，我们使用二进制优化。

# 多重背包问题

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

#### 输入格式

第一行两个整数，`N`，`V`，用空格隔开，分别表示物品种数和背包容积。

接下来有 `N` 行，每行三个整数 `vi`,`wi`,`si`，用空格隔开，分别表示第 `i` 种物品的体积、价值和数量。

#### 输出格式

输出一个整数，表示最大价值。

#### 数据范围

`0<N,V≤100`
`0<vi,wi,si≤100`

#### 输入样例

```
4 5
1 2 3
2 4 1
3 4 3
4 5 2
```

#### 输出样例：

```
10
```

## 基本思考框架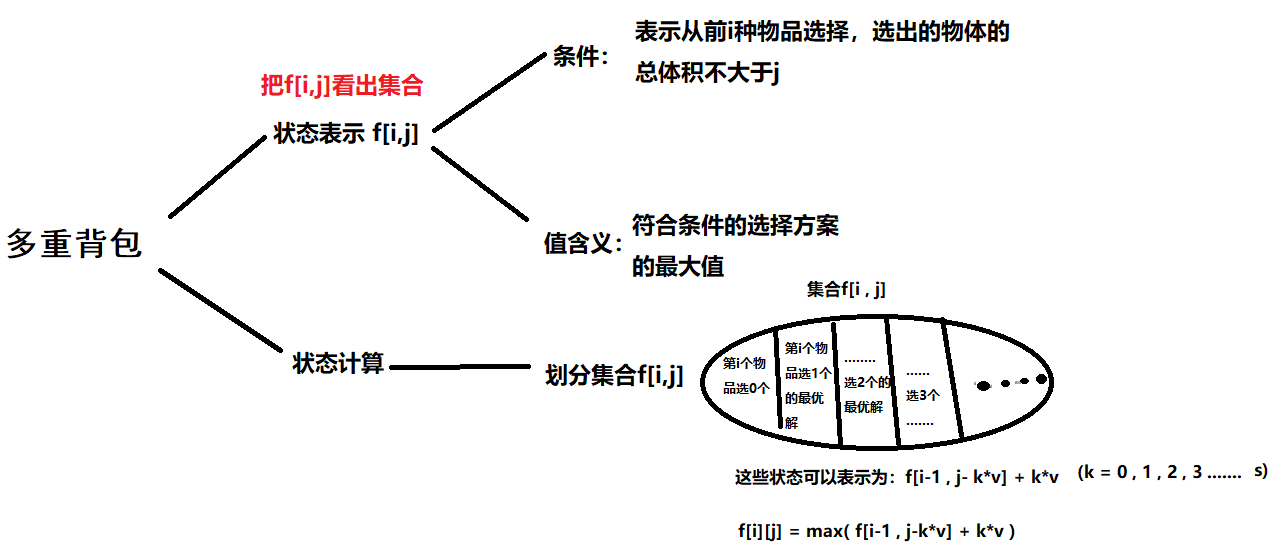

![](https://blog.fivk.cn/usr/uploads/2022/01/2311715602.png)

## 暴力写法

直接枚举所有个数的条件：

```cpp
#include <bits/stdc++.h>
using namespace std;

const int N = 110;
int v[N], w[N], s[N];
int f[N][N];
int n, m;

int main() {
    cin >> n >> m;
  
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];	// 体积、价值、数量
  
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            for (int k = 0; k <= s[i] && k * v[i] <= j; k++)	// 暴力枚举可拿数量
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);   // 找到可拿最优 
  
    cout << f[n][m];
    return 0;
}
```

当数据过大时会超时。

## 优化分析

**首先**，我们不能用完全背包的优化思路来优化这个问题，因为每组的物品的个数都不一样，是不能像之前一样推导不优化递推关系的。（详情看下面引用的博文）

> 引用我之前写的博客：动态规划-完全背包问题
>
> 我们列举一下更新次序的内部关系：
>
> f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2v]+2w , f[i-1,j-3v]+3w , .....)
> f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2v] + w , f[i-1,j-2v]+2*w , .....)
> 由上两式，可得出如下递推关系：
> f[i][j]=max(f[i,j-v]+w , f[i-1][j])

接下来，我介绍一个**二进制优化的方法**，假设有一组商品，一共有11个。我们知道，十进制数字 11 可以这样表示

$$
11=1011(B)=0111(B)+(11−0111(B))=0111(B)+0100(B)

正常背包的思路下，我们要求出含这组商品的最优解，我们要枚举12次（枚举装0，1，2....12个）。

现在，如果我们把这11个商品分别打包成含商品个数为1个，2个，4个，4个（分别对应0001,0010,0100,0100）的四个”新的商品 “, 将问题转化为01背包问题，对于每个商品，我们都只枚举一次，那么我们只需要枚举四次 ，就可以找出这含组商品的最优解。 这样就大大减少了枚举次数。

这种优化对于大数尤其明显，例如有1024个商品，在正常情况下要枚举1025次 ， 二进制思想下转化成01背包只需要枚举10次。

## 优化的合理性的证明

### 证明方法1

先讲结论：上面的1，2，4，4是可以通过组合来表示出0~11中任何一个数的，还是拿11证明一下（举例一下）：

首先，11可以这样分成两个二进制数的组合：

$$
11=0111(B)+(11−0111(B))=0111(B)+0100(B)

其中0111通过枚举这三个1的取或不取（也就是对0001(B)，0010(B)，0100(B)的组合），可以表示十进制数0 ~ 7( 刚好对应了 1，2，4 可以组合出 0 7 ) , 0 ~ 7的枚举再组合上0100(B)( 即 十进制的 4 ) ，可以表示十进制数 0~11。其它情况也可以这样证明。这也是为什么，这个完全背包问题可以等效转化为01背包问题，有木有觉得很奇妙

### 证明方法2

我们首先确认三点：

（1）我们知道转化成01背包的基本思路就是：判断每件物品我是取了你好呢还是不取你好。

（2）我们知道任意一个实数可以由二进制数来表示，也就是$2^0$ ~ $ 2^k$其中一项或几项的和。

（3）这里多重背包问的就是每件物品取多少件可以获得最大价值。

分析：

- 如果直接遍历转化为01背包问题，是每次都拿一个来问，取了好还是不取好。那么根据数据范围，这样的时间复杂度是$O(n^3)$,也就是1e+9，这样是毫无疑问是会TLE的。
- 假如10个取7个好，那么在实际的遍历过程中在第7个以后经过状态转移方程其实已经是选择“不取”好了。现在，用二进制思想将其分堆，分成k+1个分别有$2^k$个的堆，然后拿这一堆一堆去问，我是取了好呢，还是不取好呢，经过dp选择之后，结果和拿一个一个来问的结果是完全一样的，因为dp选择的是最优结果，而根据第二点任意一个实数都可以用二进制来表示，如果最终选出来10个取7个是最优的在分堆的选择过程中分成了$2^0=1,2^1=2,2^2=4,10 - 7 = 3$这四堆，然后去问四次，也就是拿去走dp状态转移方程，走的结果是第一堆1个，取了比不取好，第二堆2个，取了比不取好，第三堆四个，取了比不取好，第四堆8个，取了还不如不取，最后依旧是取了1+2+4=7个。

如果仍然不是很能理解的话，取这样一个例子:要求在一堆苹果选出n个苹果。我们传统的思维是一个一个地去选，选够n个苹果就停止。这样选择的次数就是n次

二进制优化思维就是：现在给出一堆苹果和10个箱子，选出n个苹果。将这一堆苹果分别按照1,2,4,8,16,.....512分到10个箱子里，那么由于任何一个数字x ∈[1,1024]
都可以从这10个箱子里的苹果数量表示出来，但是这样选择的次数就是 ≤10次 。

这样利用二进制优化，时间复杂度就从$O(n^3)$降到$O(n^2logS)$,从$4*10^9$降到了$2*10^7$。

</div>

## 怎么合理划分一个十进制数?

上面我把11划分为

> 11=0111(B)+(11−0111(B))=0111(B)+0100(B)

是因为 0111(B)刚好是小于11的最大的尾部全为1的二进制 ( 按照上面的证明，这样的划分没毛病 ) , 然后那个尾部全为1的数又可以 分解为 0000....1 , 0000....10 , 0000....100 等等。

对应代码：

```cpp
//设有s个商品，也就是将s划分
for (int k = 1; k <= s; k *= 2) {
	cnt++;
	v[cnt] = a * k;
	w[cnt] = b * k;
	s -= k;
}

if (s > 0) {
	cnt++;
	v[cnt] = a * s;
	v[cnt] = b * s;
}
```

## 终极AC代码

```cpp
#include<iostream>
using namespace std;

const int N = 12010, M = 2010;

int n, m;
int v[N], w[N]; //逐一枚举最大是N*logS
int f[M]; // 体积<M

int main()
{
    cin >> n >> m;
    int cnt = 0; //分组的组别
    for(int i = 1; i <= n; i ++)
    {
        int a,b,s;
        cin >> a >> b >> s;
        int k = 1; // 组别里面的个数
        while(k <= s)
        {
            cnt ++ ; //组别先增加
            v[cnt] = a * k ; //整体体积
            w[cnt] = b * k; // 整体价值
            s -= k; // s要减小
            k *= 2; // 组别里的个数增加
        }

//剩余的一组
        if(s > 0)
        {
            cnt ++ ;
            v[cnt] = a * s; 
            w[cnt] = b * s;
        }
    }

n = cnt ; //枚举次数正式由个数变成组别数

//01背包一维优化
    for(int i = 1; i <= n; i ++)
        for(int j = m ; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

cout << f[m] << endl;
    return 0;
}
```

# 后言

感觉受到降为打击。

最后修改：2022 年 01 月 07 日

如果觉得我的文章对你有用，请随意赞赏

【动态规划】多重背包

Fivk • 2022 年 01 月 06 日

# 前言

# 多重背包问题

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

#### 输入格式

第一行两个整数，`N`，`V`，用空格隔开，分别表示物品种数和背包容积。

接下来有 `N` 行，每行三个整数 `vi`,`wi`,`si`，用空格隔开，分别表示第 `i` 种物品的体积、价值和数量。

#### 输出格式

输出一个整数，表示最大价值。

#### 数据范围

`0<N,V≤100`
`0<vi,wi,si≤100`

#### 输入样例

```
4 5
1 2 3
2 4 1
3 4 3
4 5 2
```

#### 输出样例：

```
10
```

## 基本思考框架

![](https://blog.fivk.cn/usr/uploads/2022/01/2311715602.png)

## 暴力写法

直接枚举所有个数的条件：

```cpp
#include <bits/stdc++.h>
using namespace std;

const int N = 110;
int v[N], w[N], s[N];
int f[N][N];
int n, m;

当数据过大时会超时。

## 优化分析

接下来，我介绍一个**二进制优化的方法**，假设有一组商品，一共有11个。我们知道，十进制数字 11 可以这样表示

$$
11=1011(B)=0111(B)+(11−0111(B))=0111(B)+0100(B)

正常背包的思路下，我们要求出含这组商品的最优解，我们要枚举12次（枚举装0，1，2....12个）。

这种优化对于大数尤其明显，例如有1024个商品，在正常情况下要枚举1025次 ， 二进制思想下转化成01背包只需要枚举10次。

## 优化的合理性的证明

### 证明方法1

先讲结论：上面的1，2，4，4是可以通过组合来表示出0~11中任何一个数的，还是拿11证明一下（举例一下）：

首先，11可以这样分成两个二进制数的组合：

$$
11=0111(B)+(11−0111(B))=0111(B)+0100(B)

### 证明方法2

我们首先确认三点：

（1）我们知道转化成01背包的基本思路就是：判断每件物品我是取了你好呢还是不取你好。

（2）我们知道任意一个实数可以由二进制数来表示，也就是$2^0$ ~ $ 2^k$其中一项或几项的和。

（3）这里多重背包问的就是每件物品取多少件可以获得最大价值。

分析：

这样利用二进制优化，时间复杂度就从$O(n^3)$降到$O(n^2logS)$,从$4*10^9$降到了$2*10^7$。

</div>

## 怎么合理划分一个十进制数?

上面我把11划分为

> 11=0111(B)+(11−0111(B))=0111(B)+0100(B)

对应代码：

```cpp
//设有s个商品，也就是将s划分
for (int k = 1; k <= s; k *= 2) {
	cnt++;
	v[cnt] = a * k;
	w[cnt] = b * k;
	s -= k;
}

if (s > 0) {
	cnt++;
	v[cnt] = a * s;
	v[cnt] = b * s;
}
```

## 终极AC代码

```cpp
#include<iostream>
using namespace std;

const int N = 12010, M = 2010;

int n, m;
int v[N], w[N]; //逐一枚举最大是N*logS
int f[M]; // 体积<M

//剩余的一组
        if(s > 0)
        {
            cnt ++ ;
            v[cnt] = a * s; 
            w[cnt] = b * s;
        }
    }

n = cnt ; //枚举次数正式由个数变成组别数

//01背包一维优化
    for(int i = 1; i <= n; i ++)
        for(int j = m ; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

cout << f[m] << endl;
    return 0;
}
```

# 后言

感觉受到降为打击。

【动态规划】多重背包

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

这是好东西

【Fivk】文章归档

【Redis】SpringBoot项目Redis哨兵集群和单节点自适应

【Typecho】一款Hansome主题专用的UserAgent插件

【Docker】Docker部署SpringBoot项目

【知识总结】Linux部署Jar包

【代码笔记】vscode的安装与配置

【动态规划】多重背包