【动态规划】数字三角形

Fivk

2022 年 01 月 07 日

1028 次浏览

暂无评论

805字数

题目典例

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

```
        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5
```

#### 输入格式

第一行包含整数 n，表示数字三角形的层数。

接下来 n 行，每行包含若干整数，其中第 i 行表示数字三角形第 i 层包含的整数。

#### 输出格式

输出一个整数，表示最大的路径数字和。

#### 数据范围

1≤n≤500,
−10000≤三角形中的整数≤10000

#### 输入样例：

```
5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5
```

#### 输出样例：

```
30
```

#### 基本思考框架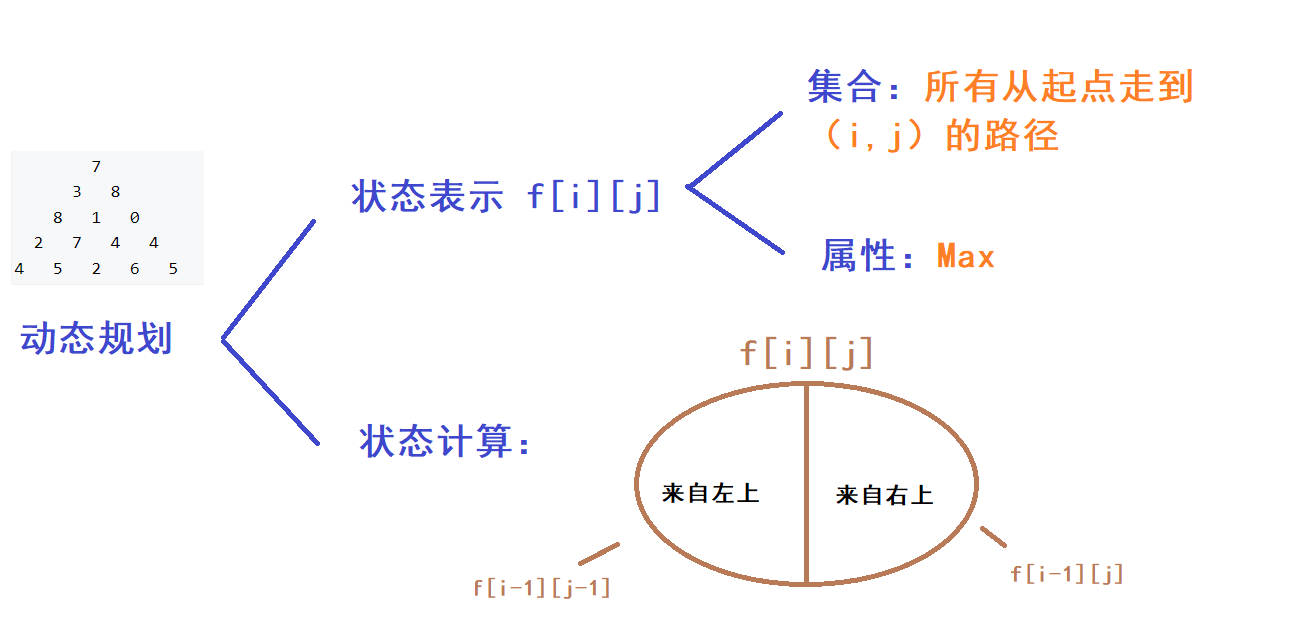

![](https://blog.fivk.cn/usr/uploads/2022/01/2903410270.png)

状态转移方程：`dp[i][j] = dp[i][j] + max(dp[i - 1][j - 1],dp[i - 1][j])`

#### 从上到下dp

```cpp
#include<bits/stdc++.h>
using namespace std;

const int N=510,INF=0x3f3f3f3f;
int f[N][N];
int a[N][N];

int main(){
    int n;
    cin>>n;

for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>a[i][j];
        }
    }

for(int i=1;i<=n;i++){       
        for(int j=0;j<=i+1;j++){          //因为有负数，所以应该将两边也设为-INF
            f[i][j]=-INF;
        }
    }

f[1][1]=a[1][1];
    for(int i=2;i<=n;i++){
        for(int j=1;j<=i;j++){
            f[i][j]=a[i][j]+max(f[i-1][j-1],f[i-1][j]);
        }
    }

int res=-INF;
    for(int i=1;i<=n;i++) res=max(res,f[n][i]);
    cout<<res<<endl;
}
```

#### 从下到上dp

更简单些，因为倒序不需要考虑边界问题

```cpp
#include <bits/stdc++.h>
using namespace std;

const int N = 510;

int n;
int a[N][N];

int main() {
    cin >> n;
  
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++)
            cin >> a[i][j];
          
    for (int i = n - 1; i >= 1; i--) 
        for (int j = 1; j <= i; j++) 
            a[i][j] = a[i][j] + max(a[i + 1][j], a[i + 1][j + 1]);
  
    cout << a[1][1];
    return 0;
}
```

最后修改：2022 年 01 月 07 日