【机器学习】单层感知机

博主： Fivk
发布时间：2022 年 01 月 08 日
1572 次浏览
暂无评论
9877字数
分类： python

# 一、感知机概述

## 1.如何理解感知机

“感”就是感受，必然要输入；“知”就是知道，一定有输出。所以感知机就可以理解为对输入进行处理，得到并输出结果的机器。

</div>

例如，一个人朝你走来，他/她的五官信息作为输入被你的眼睛感受到，然后大脑经过综合分析、处理，得到美还是丑的结论。在这个过程中，大脑就扮演着感知机的角色。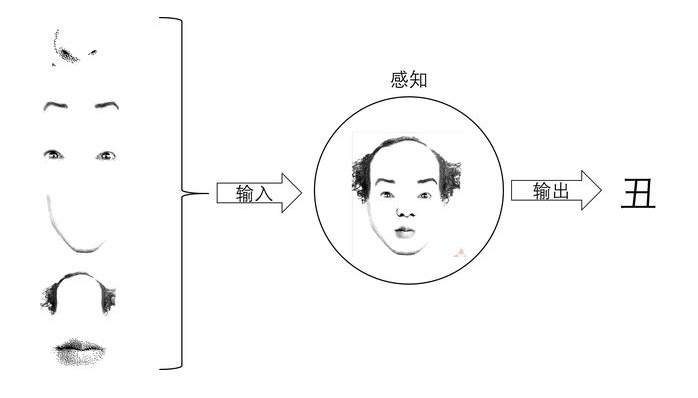

![什么是感知机.png](https://blog.fivk.cn/usr/uploads/2022/01/1846620123.png)

为什么大脑和感知机如此相像呢？其实是感知机和大脑像才对。因为先有大脑，再有的感知机。感知机最初的目的就是为了模拟大脑的这种行为的。一句话概括：

感知机就是模拟大脑感知的机器。

## 2.感知器介绍

- **感知机**（英语：Perceptron）是Frank Rosenblatt在1957年就职于Cornell航空实验室(Cornell Aeronautical Laboratory)时所发明的一种人工神经网络。它可以被视为一种最简单形式的前馈式人工神经网络，**是一种二元线性分类器**。
- Frank Rosenblatt给出了相应的感知机学习算法，常用的**有感知机学习**、**最小二乘法**和**梯度下降法**。譬如，感知机利用梯度下降法对损失函数进行极小化，求出可将训练数据进行线性划分的分离超平面，从而求得感知机模型。
- 感知机是生物神经细胞的简单抽象。神经细胞结构大致可分为：树突、突触、细胞体及轴突。单个神经细胞可被视为一种只有两种状态的机器——激动时为‘是’，而未激动时为‘否’。神经细胞的状态取决于从其它的神经细胞收到的输入信号量，及突触的强度（抑制或加强）。当信号量总和超过了某个阈值时，细胞体就会激动，产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。为了模拟神经细胞行为，与之对应的感知机基础概念被提出，如权量（突触）、偏置（阈值）及激活函数（细胞体）。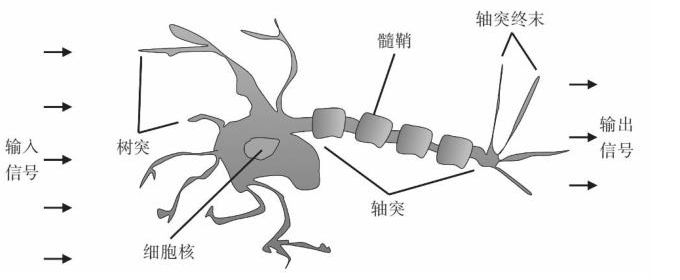

![结构图.png](https://blog.fivk.cn/usr/uploads/2022/01/4161490567.png)

在人工神经网络领域中，感知机也被指为单层的人工神经网络，以区别于较复杂的多层感知机（Multilayer Perceptron）。 作为一种线性分类器，（单层）感知机可说是最简单的前向人工神经网络形式。尽管结构简单，感知机能够学习并解决相当复杂的问题。感知机主要的本质缺陷是它不能处理线性不可分问题。

线性分类器的第一个迭代算法是1956年由Frank Rosenblatt提出的。这个算法被提出后，受到了很大的关注。感知器在神经网络发展的历史上占据着特殊的位置：它是第一个从算法上完整描述的神经网络。在20世纪60年代和70年代，受感知器的启发，工程师、物理学家以及数学家们纷纷投身于神经网络不同方面的研究。这个算法在今天看来依然是有效的。

# 二、计算步骤

## 算法图解

设有 `n`维（特征数）输入的单个感知机（如下图所示），`X1`至 `X2`为 `n`维输入向量的各个分量，`W1`至 `W2`为各个输入分量连接到感知机的权量（或称权值），`W0`为偏置，激活函数（又称激励函数或传递函数），`Z`为标量输出（也称为净输入）。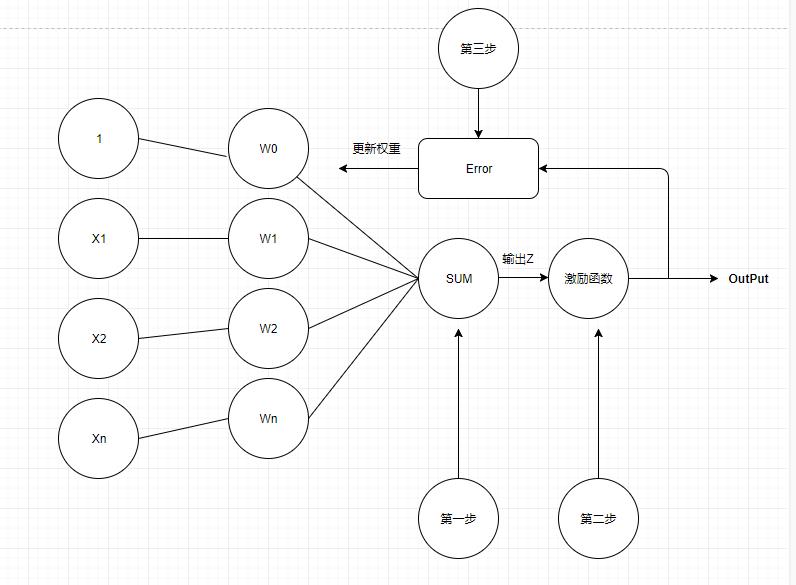

![算法图解.jpg](https://blog.fivk.cn/usr/uploads/2022/01/1131604431.jpg)

## 第一步

这里 `Z`称为净输入（`net input`），它的值等于一个样本的每个维度值 `X`与维度对应的权重值w相乘后的和。

$$
\begin{aligned}
    Z &= W_1 * X_1 + W_2 * X_2 + ... + W_n * X_n\\
      &=\sum_{j=1}^nW_j*X_j\\
      &=W^T*X
\end{aligned}

## 第二步

计算结果 `Z`是一个连续的值，我们需要将结果转换为离散的分类值，因此，这里，我们使用一个转换函数，该函数称为激励函数（激活函数），这里 `θ`就是阈值。

$$
step(z) = 
\begin{cases}
\text{1},  & \text{Z $\ge$ $\theta$} \\
\text{0}, & \text{z $\lt$ $\theta$}
\end{cases}

## 第三步

**更新权重**
感知器是一个自学习算法，即可以根据输入的数据（样本），不断调整权重的更新，最终完成分类。对于权重的更新公式如下：

$$
W_j = W_j + \Delta

$$
\Delta W_j = \eta(y^i-\hat{y}^i)x_j^i

其中：

- `j`表示某一列
- `i`表示某一个样本
- $\eta$：学习速率（一个介于0.0到1.0之间的常数）
- $y(i)$：是第i个样本的真实类标（即真实值）
- $y^i$：是第i个样本的预测类标（预测值）。需要注意的是，权重向量中的所有权重值是同时更新的，这意味着在所有的权重 $\Delta w_j$ 更新前，我们无法重新计算$y^i$。
- 这里的i和j怎么理解？每次计算`Z`是同一个样本的维度值和权重值相乘之和，每次更新权重值会对每个权重值进行更新。
- 类标是什么？类标就是分类的标签，在这里类标就是1或者0。

## 更新原则

**感知器的权重更新依据是：如果预测准确，则权重不进行更新，否则，增加权重，使其更趋向于正确的类别。**
以下介绍感知器的推到过程（内核），体验一下感知器规则的简洁之美。

### 1.对于如下所示的两种场景，若感知器对类标的预测正确，权重可不做更新：

$$
\Delta w_j = \eta(-1^i-(-1)^i)x_j^i=0

$$
w_j = \eta(1^i-i^i)x_j^i=0

### 2.在类标预测错误的情况下，权重的值会分别趋向于正类别或者负类别的方向

$$
\Delta w_j = \eta(-1^i-i^i)x^i_j=-2{\eta}x^i_j

$$
\Delta w_j = \eta(1^i-(-1)^i)x_j^i=2\eta x^i_j

### 3.解释

假定

$$
x^i_j = 0.5

且模型将此样本错误的分类到了-1类别内。再此情况下，我们应将相应的权值增1，以保证下次遇到此样本时使得激活函数

$$
x^i_j=w^i_j

能够将其更多的判定为正类别，这也相当于增大其值大于单位阶跃函数阈值的概率，以便得样本被判定为+1类

$$
\Delta w^i_j=(1^i-(-1)^i)*0.5^i=2*0.5=1

权重的更新与$x^i_j=0.5$成比例。例如另外一个样本$x_j^i=2$被错误的分类到-1类别中，我们应更大幅度的移动决策边界，以保证下次遇到此类样本时能正确分类。

$$
\Delta w_j^i = (1^i-(-1)^i)*2^i=2*2=4

# 三、Python算法实现

1.对权重进行初始化。（初始化为0或者很小的数值。）
2.对训练集中每一个样本进行迭代，计算输出值y。

- 根据输出值y与真实值，更新权重。
- 循环步骤2。直到达到指定的次数（或者完全收敛）。

**说明：**

如果两个类别线性可分，则感知器一定会收敛。
如果两个类别线性不可分，则感知器一定不会收敛。
感知器收敛的前提是两个类别必须是线性可分的，且学习速率足够小。
如果两个类别无法通过一个线性决策边界进行划分，可以为模型在训练数据集上的学习迭代次数设置一个最大值， 或者设置一个允许错误分类样本数量的阈值，否则，感知器训练算法将永远不停的更新权值。

</div>

## 感知器的基础算法

```python
import pandas as pd
import numpy as np
import  matplotlib.pyplot as plt

class Perceptron(object):
    """Perceptron classifier.
    参数：
    eta (学习率): float，取值范围0.0-1.0
    n_iter（在训练集进行迭代的次数） : int
    random_state （随机数产生器的种子）: int
    属性：
    w_ （权重）: ，np一维数组
    errors_ （存储每轮训练集判断错误的次数）: list
    """
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

def fit(self, X, y):
        """Fit training data.
        Parameters
        ----------
        X : 二维np数组,形式：[[样本1维度值1，样本1维度值2...],[样本2维度值1，样本2维度值2...],...]
        y : 一维np数组，形式：[样本1的类标],样本2的类标，...]

Returns
        -------
        self : object

"""
        #设置随机数种子
        rgen = np.random.RandomState(self.random_state)
        #生成正态分布的随机数,权重w
        self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
        self.errors_ = []

for _ in range(self.n_iter):
            # 迭代所有样本，并根据感知器规则来更新权重
            errors = 0
            for xi, target in zip(X, y):
                # print(xi,target)
                update = self.eta * (target - self.predict(xi)) #更新权重值
                self.w_[0] += update
                self.w_[1:] += update * xi
                #预测错误：update如果不为0，则表示判断错误
                errors += int(update != 0.0)
            self.errors_.append(errors)
        return self

#计算z的函数
    def net_input(self, X):
        """Calculate net input"""
        # ϕ(z) = w0 * 1 + w1∗x1 + w2∗x2 + ... + wm∗xm
        z = self.w_[0] * 1 + np.dot(X, self.w_[1:])
        return z

#阈值函数
    def predict(self, X):
        """Return class label after unit step"""
        return np.where(self.net_input(X) >= 0.0, 1, -1)

df = pd.read_csv('https://archive.ics.uci.edu/ml/'
        'machine-learning-databases/iris/iris.data', header=None)
print(df.tail())
# select setosa and versicolor
#选择0-100行的第5列数据
y = df.iloc[0:100, 4].values
#0-100行中，选择第5列的列名为Iris-setosa的数据做处理，如果
y = np.where(y == 'Iris-setosa', -1, 1)
# [1,1,1,1,1,...-1,-1,-1]
# extract sepal length and petal length
X = df.iloc[0:100, [0, 2]].values
ppn = Perceptron(eta=0.1, n_iter=10)
#训练数据
ppn.fit(X, y)
#迭代次数与每次迭代时预测错误的次数作图
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of updates')
plt.savefig('运行图片/1.png', dpi=300)
# plt.show()
```

[album type="photos"]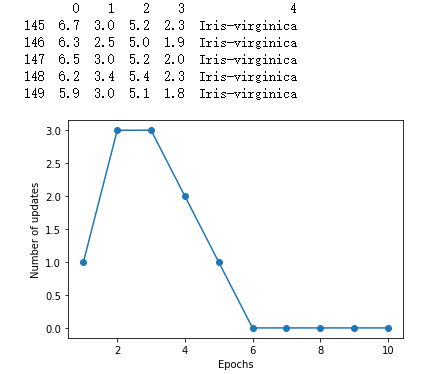

![运行结果](https://blog.fivk.cn/usr/uploads/2022/01/3376338678.png)
[/album] </div>

## 怎么判断感知器是否收敛

```python
import pandas as pd
import numpy as np
import  matplotlib.pyplot as plt

"""
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

Returns
        -------
        self : object

for _ in range(self.n_iter):
            # 迭代所有样本，并根据感知器规则来更新权重
            errors = 0
            for xi, target in zip(X, y):
                # print(xi,target)
                update = self.eta * (target - self.predict(xi))
                self.w_[0] += update
                self.w_[1:] += update * xi
                #预测错误：update如果不为0，则表示判断错误
                errors += int(update != 0.0)
            self.errors_.append(errors)
        return self

#阈值函数
    def predict(self, X):
        """Return class label after unit step"""
        return np.where(self.net_input(X) >= 0.0, 1, -1)

df = pd.read_csv('https://archive.ics.uci.edu/ml/'
        'machine-learning-databases/iris/iris.data', header=None)
# print(df.tail())
# select setosa and versicolor
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
# extract sepal length and petal length
X = df.iloc[0:100, [0, 2]].values
# plot data
ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of updates')

plt.savefig('运行图片/2.png', dpi=300)
# plt.show()
```

[album type="photos"]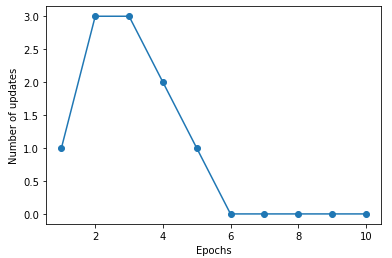

![运行结果](https://blog.fivk.cn/usr/uploads/2022/01/3403638049.png)

[/album] </div>

## 怎么判断两个类别是否线性可分

使用散点图显示两个类别的两个维度

```python
import pandas as pd
import  matplotlib.pyplot as plt

df = pd.read_csv('https://archive.ics.uci.edu/ml/'
        'machine-learning-databases/iris/iris.data', header=None)
print(df.tail())
# extract sepal length and petal length
X = df.iloc[0:100, [0, 2]].values
# plot data
plt.scatter(X[:50, 0], X[:50, 1],
            color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1],
            color='blue', marker='x', label='versicolor')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.savefig('运行图片/3.png', dpi=300)
plt.show()
```

[album type="photos"]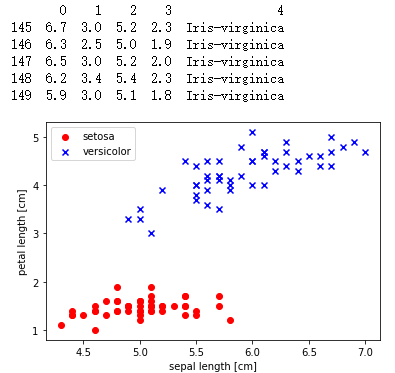

![运行图片](https://blog.fivk.cn/usr/uploads/2022/01/2797884104.png)
[/album] </div>

**参考：**

- [https://blog.csdn.net/qq_42442369/article/details/87613450](https://blog.csdn.net/qq_42442369/article/details/87613450)
- [https://blog.csdn.net/u012806787/article/details/80116098](https://blog.csdn.net/u012806787/article/details/80116098)
- [https://blog.csdn.net/xylin1012/article/details/71931900](https://blog.csdn.net/xylin1012/article/details/71931900)
- [https://blog.csdn.net/yawdeep/article/details/78827088](https://blog.csdn.net/yawdeep/article/details/78827088)

最后修改：2022 年 01 月 25 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

本当迷
哈哈时过境迁再看一遍帆的文章质量还是那么高
挺胸的打工人
感谢博主分享
菜菜
一天就学一些我不知道的东西(´இ皿இ｀)
zhanqy
博主赛高！
null ？？［］
还可以把扩展运算符加上呀，这个很有用［…arr］，用于数组合...

【机器学习】单层感知机

Fivk • 2022 年 01 月 08 日

# 一、感知机概述

## 1.如何理解感知机

“感”就是感受，必然要输入；“知”就是知道，一定有输出。所以感知机就可以理解为对输入进行处理，得到并输出结果的机器。

</div>

![什么是感知机.png](https://blog.fivk.cn/usr/uploads/2022/01/1846620123.png)

感知机就是模拟大脑感知的机器。

## 2.感知器介绍

![结构图.png](https://blog.fivk.cn/usr/uploads/2022/01/4161490567.png)

# 二、计算步骤

## 算法图解

![算法图解.jpg](https://blog.fivk.cn/usr/uploads/2022/01/1131604431.jpg)

## 第一步

这里 `Z`称为净输入（`net input`），它的值等于一个样本的每个维度值 `X`与维度对应的权重值w相乘后的和。

$$
\begin{aligned}
    Z &= W_1 * X_1 + W_2 * X_2 + ... + W_n * X_n\\
      &=\sum_{j=1}^nW_j*X_j\\
      &=W^T*X
\end{aligned}

## 第二步

$$
step(z) = 
\begin{cases}
\text{1},  & \text{Z $\ge$ $\theta$} \\
\text{0}, & \text{z $\lt$ $\theta$}
\end{cases}

## 第三步

**更新权重**
感知器是一个自学习算法，即可以根据输入的数据（样本），不断调整权重的更新，最终完成分类。对于权重的更新公式如下：

$$
W_j = W_j + \Delta

$$
\Delta W_j = \eta(y^i-\hat{y}^i)x_j^i

其中：

## 更新原则

### 1.对于如下所示的两种场景，若感知器对类标的预测正确，权重可不做更新：

$$
\Delta w_j = \eta(-1^i-(-1)^i)x_j^i=0

$$
w_j = \eta(1^i-i^i)x_j^i=0

### 2.在类标预测错误的情况下，权重的值会分别趋向于正类别或者负类别的方向

$$
\Delta w_j = \eta(-1^i-i^i)x^i_j=-2{\eta}x^i_j

$$
\Delta w_j = \eta(1^i-(-1)^i)x_j^i=2\eta x^i_j

### 3.解释

假定

$$
x^i_j = 0.5

且模型将此样本错误的分类到了-1类别内。再此情况下，我们应将相应的权值增1，以保证下次遇到此样本时使得激活函数

$$
x^i_j=w^i_j

能够将其更多的判定为正类别，这也相当于增大其值大于单位阶跃函数阈值的概率，以便得样本被判定为+1类

$$
\Delta w^i_j=(1^i-(-1)^i)*0.5^i=2*0.5=1

$$
\Delta w_j^i = (1^i-(-1)^i)*2^i=2*2=4

# 三、Python算法实现

1.对权重进行初始化。（初始化为0或者很小的数值。）
2.对训练集中每一个样本进行迭代，计算输出值y。

- 根据输出值y与真实值，更新权重。
- 循环步骤2。直到达到指定的次数（或者完全收敛）。

**说明：**

</div>

## 感知器的基础算法

```python
import pandas as pd
import numpy as np
import  matplotlib.pyplot as plt

Returns
        -------
        self : object

#阈值函数
    def predict(self, X):
        """Return class label after unit step"""
        return np.where(self.net_input(X) >= 0.0, 1, -1)

[album type="photos"]

![运行结果](https://blog.fivk.cn/usr/uploads/2022/01/3376338678.png)
[/album] </div>

## 怎么判断感知器是否收敛

```python
import pandas as pd
import numpy as np
import  matplotlib.pyplot as plt

"""
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

Returns
        -------
        self : object

#阈值函数
    def predict(self, X):
        """Return class label after unit step"""
        return np.where(self.net_input(X) >= 0.0, 1, -1)

plt.savefig('运行图片/2.png', dpi=300)
# plt.show()
```

[album type="photos"]

![运行结果](https://blog.fivk.cn/usr/uploads/2022/01/3403638049.png)

[/album] </div>

## 怎么判断两个类别是否线性可分

使用散点图显示两个类别的两个维度

```python
import pandas as pd
import  matplotlib.pyplot as plt

[album type="photos"]

![运行图片](https://blog.fivk.cn/usr/uploads/2022/01/2797884104.png)
[/album] </div>

**参考：**

【机器学习】单层感知机

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

【Fivk】文章归档

回忆刚入天柱二中的我

【Java】常用类之包装类

【前端笔记】CSS3

【算法基础】高精度加法（C++描述）

可算来了

【c】利用二维数组转置行列式

【机器学习】单层感知机

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【机器学习】单层感知机

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款