Loading... ### 简介 如果扩展到二维,我们需要让二维数组被选中的子矩阵中的每个元素的值加上`c`,是否也可以达到`O(1)`的时间复杂度。答案是可以的,**考虑二维差分。** `a[][]`数组是`b[][]`数组的前缀和数组,那么`b[][]`是`a[][]`的差分数组 原数组: `a[i][j]` 我们去构造差分数组: `b[i][j]` 使得`a`数组中`a[i][j]`是`b`数组左上角`(1,1)`到右下角`(i,j)`所包围矩形元素的和。 ### 如何构造`b`数组呢? 我们去**逆向思考**。 同一维差分,我们构造二维差分数组目的是为了 让原二维数组`a`中所选中子矩阵中的每一个元素加上c的操作,可以由`O(n*n)`的时间复杂度优化成`O(1)` 已知原数组`a`中被选中的子矩阵为 以`(x1,y1)`为左上角,以`(x2,y2)`为右下角所围成的矩形区域; **始终要记得,`a`数组是`b`数组的前缀和数组**,比如对`b`数组的`b[i][j]`的修改,会影响到`a`数组中从`a[i][j]`及往后的每一个数。 假定我们已经构造好了`b`数组,类比一维差分,我们执行以下操作 来使被选中的子矩阵中的每个元素的值加上`c` `b[x1][y1] += c;` `b[x1][y2+1] -= c;` `b[x2+1][y1] -= c;` `b[x2+1][y2+1] += c;` 每次对`b`数组执行以上操作,**等价于**: ```cpp for(int i=x1;i<=x2;i++) for(int j=y1;j<=y2;j++) a[i][j]+=c; ``` **我们画个图去理解一下这个过程:** 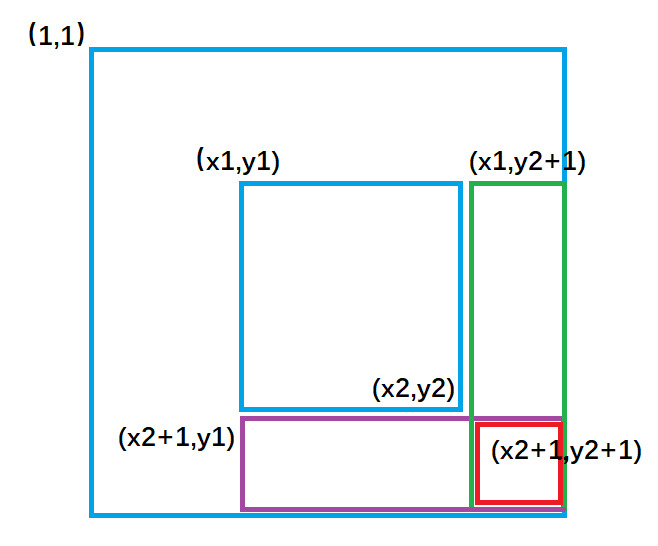 `b[x1][ y1 ] += c ;` 对应图1 ,让整个`a`数组中蓝色矩形面积的元素都加上了`c`。 `b[x1,][y2+1] -= c ;`对应图2 ,让整个`a`数组中绿色矩形面积的元素再减去`c`,使其内元素不发生改变。 `b[x2+1][y1] -= c ;`对应图3 ,让整个`a`数组中紫色矩形面积的元素再减去`c`,使其内元素不发生改变。 `b[x2+1][y2+1] += c;` 对应图4 ,让整个`a`数组中红色矩形面积的元素再加上`c`,红色内的相当于被减了两次,再加上一次`c`,才能使其恢复。  **我们将上述操作封装成一个插入函数:** ```cpp void insert(int x1,int y1,int x2,int y2,int c) { //对b数组执行插入操作,等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c b[x1][y1]+=c; b[x2+1][y1]-=c; b[x1][y2+1]-=c; b[x2+1][y2+1]+=c; } ``` 我们可以先假想`a`数组为空,那么`b`数组一开始也为空,但是实际上`a`数组并不为空,因此我们每次让以`(i,j)`为左上角到以`(i,j)`为右上角面积内元素(其实就是一个小方格的面积)去插入 `c=a[i][j]`,等价于原数组`a`中`(i,j)` 到`(i,j)`范围内 加上了 `a[i][j]` ,因此执行`n*m`次插入操作,就成功构建了差分`b`数组. **代码如下:** ```cpp for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { insert(i,j,i,j,a[i][j]); //构建差分数组 } } ``` **总结:**  ### AC代码 ```cpp #include<iostream> #include<cstdio> using namespace std; const int N = 1e3 + 10; int a[N][N], b[N][N]; void insert(int x1, int y1, int x2, int y2, int c) { b[x1][y1] += c; b[x2 + 1][y1] -= c; b[x1][y2 + 1] -= c; b[x2 + 1][y2 + 1] += c; } int main() { int n, m, q; cin >> n >> m >> q; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) cin >> a[i][j]; for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { insert(i, j, i, j, a[i][j]); //构建差分数组 } } while (q--) { int x1, y1, x2, y2, c; cin >> x1 >> y1 >> x2 >> y2 >> c; insert(x1, y1, x2, y2, c); } for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //二维前缀和 } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { printf("%d ", b[i][j]); } printf("\n"); } return 0; } ``` 最后修改:2021 年 12 月 06 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 1 如果觉得我的文章对你有用,请随意赞赏