Loading... 昨天晚上做了那个哈夫曼算法的题,今天没有考。qvq 现在来看看今天的编程题: ### R6-1 实现基于邻接矩阵表示的深度优先遍历 (20 分) 实现基于邻接矩阵表示的深度优先遍历。 ### 函数接口定义: ```c void DFS(Graph G, int v); ``` 其中 `G` 是基于邻接矩阵存储表示的无向图,`v`表示遍历起点。 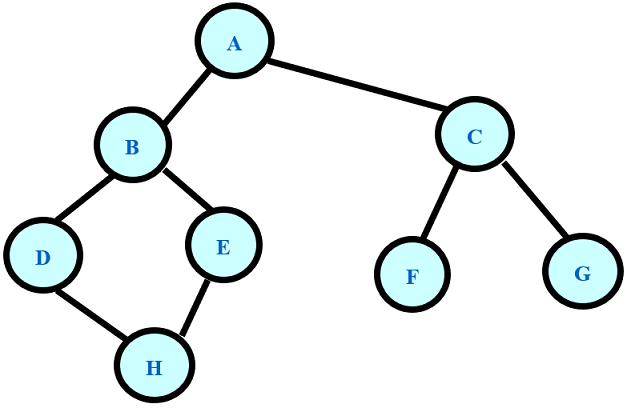 ### 裁判测试程序样例: ```c #include <stdio.h> #include <stdlib.h> #define MVNum 10 int visited[MVNum]; typedef struct{ char vexs[MVNum]; int arcs[MVNum][MVNum]; int vexnum,arcnum; }Graph; void CreateUDN(Graph &G);//实现细节隐藏 void DFS(Graph G, int v); void DFSTraverse(Graph G){ int v; for(v = 0; v < G.vexnum; ++v) visited[v] = 0; for(v = 0; v < G.vexnum; ++v) if(!visited[v]) DFS(G, v); } int main(){ Graph G; CreateUDN(G); DFSTraverse(G); return 0; } /* 请在这里填写答案 */ ``` ### 输入样例: 输入第1行为结点数vexnum和边数arcnum。第2行为结点的值,依次输入arcnum行,每行输入两个结点的值表示该两个结点互为邻接点。 ```in 8 8 ABCDEFGH A B A C B D B E C F C G D H E H ``` ### 输出样例: 遍历序列。 ```out A B D H E C F G ``` ### 我的程序(不知道对不对,先保留): ```c void CreateUDN(Graph& G) { scanf("%d %d", &G.vexnum, &G.arcnum); scanf("%s", G.vexs); for (int i = 0; i < G.vexnum; i++) for (int j = 0; j < G.arcnum; j++) G.arcs[i][j] = 0; for (int i = 0; i < G.arcnum; i++) { getchar(); int x = 0, y = 0; char c1, c2; scanf("%c %c", &c1, &c2); for (int j = 0; j < G.vexnum; j++) { // 找到第一个字符的位置 if (c1 == G.vexs[j]) { x = j; break; } } for (int j = 0; j < G.vexnum; j++) { // 找到第二个字符的位置 if (c2 == G.vexs[j]) { y = j; break; } } G.arcs[x][y] = G.arcs[y][x] = 1; // 表示无向图连通 } } void DFS(Graph G, int v) { printf("%c ", G.vexs[v]); visited[v] = 1; for (int i = 0; i < G.vexnum; i++) { if (!visited[i] && G.arcs[v][i]) { DFS(G, i); } } } ```  ### 我的AC笔记: ```c #include <stdio.h> #include <stdlib.h> #define MVNum 10 int visited[MVNum]; typedef struct { char vexs[MVNum]; int arcs[MVNum][MVNum]; int vexnum, arcnum; }Graph; void CreateUDN(Graph& G);//实现细节隐藏 void DFS(Graph G, int v); void DFSTraverse(Graph G) { int v; for (v = 0; v < G.vexnum; ++v) visited[v] = 0; for (v = 0; v < G.vexnum; ++v) if (!visited[v]) DFS(G, v); } int main() { Graph G; CreateUDN(G); for (int i = 0; i < G.vexnum; i++) { for (int j = 0; j < G.arcnum; j++) { printf("%d ", G.arcs[i][j]); } printf("\n"); } DFSTraverse(G); return 0; } /* 请在这里填写答案 */ /* 输入第1行为结点数vexnum和边数arcnum。 第2行为结点的值,依次输入arcnum行,每行输入两个结点的值表示该两个结点互为邻接点。 */ /* 8 8 ABCDEFGH A B A C B D B E C F C G D H E H */ void CreateUDN(Graph& G) { scanf("%d %d", &G.vexnum, &G.arcnum); //getchar(); scanf("%s", G.vexs); for (int i = 0; i < G.vexnum; i++) for (int j = 0; j < G.arcnum; j++) G.arcs[i][j] = 0; //printf("\n"); for (int i = 0; i < G.arcnum; i++) { getchar(); int x = 0, y = 0; char c1, c2; scanf("%c %c", &c1, &c2); for (int j = 0; j < G.vexnum; j++) { // 找到第一个字符的位置 if (c1 == G.vexs[j]) { x = j; break; } } //printf("%c ", ch); //scanf("%c\n", &ch); for (int j = 0; j < G.vexnum; j++) { // 找到第二个字符的位置 if (c2 == G.vexs[j]) { y = j; break; } } //printf("%c ", ch); G.arcs[x][y] = G.arcs[y][x] = 1; // 表示无向图连通 //printf("%c %c : x = %d , y = %d\n", c1, c2, x, y); } } void DFS(Graph G, int v) { printf("%c ", G.vexs[v]); visited[v] = 1; for (int i = 0; i < G.vexnum; i++) { if (!visited[i] && G.arcs[v][i]) { //printf("%d\n", i); DFS(G, i); } } } ``` 最后修改:2021 年 11 月 12 日 © 禁止转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏
2 条评论
c++大佬啊,带我飞啊
大佬不敢当,就是日常应付作业