【算法基础】最短距离Dijkstra

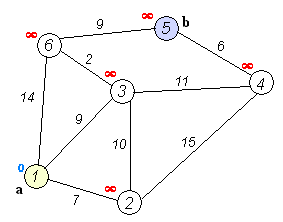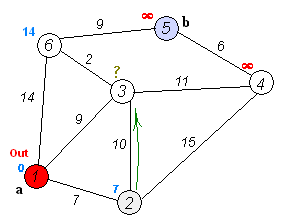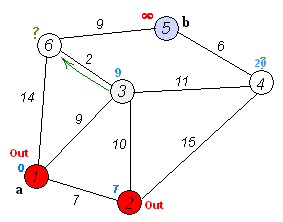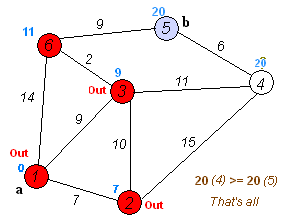![dijkstra图示](https://blog.fivk.cn/usr/uploads/2022/02/3043025892.jpg)

因为之前已经介绍过了，现在就不仔细介绍了，直接上算法。

<div class="inner-content" >
<p class="inser-title">【数据结构】图论算法_最短路径算法</p>
<div class="inster-summary text-muted">
如图所示，我们把边带有权值的图称为带权图。边的权值可以理解为两点之间的距离。一张图中任意两点中的距离会有不同的路径...
</div>
</div>
</a>

</div>

</div>

# 朴素版

从`s`到`t`的最短距离算法流程：

`b[]`表示当前已经确定最短距离的点。

1. `dis[s] = 0, dis[其他] = +∞`
2. for (int i = 1; i <= n; i ++)
   * `t`：不在`b`中的最短距离的点
   * 将`t`加入`b[]`
   * 使用`t`更新其他未被确定的点的距离

#### 代码实现

```cpp
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 510;

int n, m;
int w[N][N];
int dis[N];
bool b[N];

int dijkstra() {
	memset(dis, 0x3f, sizeof dis);
	dis[1] = 0;

for (int i = 0; i < n; i ++) {
		int k = -1;
		for (int j = 1; j <= n; j ++)
			if (!b[j] && (k == -1 || dis[k] > dis[j]))
				k = j;

b[k] = true;

for (int j = 1; j <= n; j ++) {
			dis[j] = min(dis[j], dis[k] + w[k][j]);
		}
	}

if (dis[n] == 0x3f3f3f3f) return -1;
	else return dis[n];
}

int main() {
	scanf("%d %d", &n, &m);

memset(w, 0x3f, sizeof w);

while (m --) {
		int i, j, k;
		scanf("%d %d %d", &i, &j, &k);
		w[i][j] = min(w[i][j], k);
	}

int t = dijkstra();

printf("%d", t);
	return 0;
}
```

# 堆优化版

最后修改：2022 年 02 月 27 日

如果觉得我的文章对你有用，请随意赞赏

【算法基础】最短距离Dijkstra

Fivk • 2022 年 02 月 27 日

【算法基础】最短距离Dijkstra

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

这是好东西

【Fivk】文章归档

【知识总结】动态规划合集

中秋遇到国庆

【数据结构】PTA 公路村村通（最小生成树Prim算法引入）

此内容被密码保护

【Tool】Docker部署青龙面板

【算法基础】最短距离Dijkstra