【题目典例】分巧克力

### 题目描述

儿童节那天有 `K` 位小朋友到小明家做客。

小明拿出了珍藏的巧克力招待小朋友们。

小明一共有 `N` 块巧克力，其中第 `i` 块是 $H_i×W_i$ 的方格组成的长方形。

为了公平起见，小明需要从这 `N` 块巧克力中切出 `K` 块巧克力分给小朋友们。

切出的巧克力需要满足：

1. 形状是正方形，边长是整数
2. 大小相同

例如一块 `6×5` 的巧克力可以切出 `6` 块 `2×2` 的巧克力或者 `2` 块 `3×3` 的巧克力。

当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

### 输入格式

第一行包含两个整数 `N` 和 `K`。

以下 `N` 行每行包含两个整数 $H_i$ 和 $W_ i$。

输入保证每位小朋友至少能获得一块 $1×1$ 的巧克力。

### 输出格式

输出切出的正方形巧克力最大可能的边长。

### 数据范围

$1≤N,K≤10^5$
$1≤H_i,W_i≤10^5$

### 输入样例：

```
2 10
6 5
5 6
```

### 输出样例：

```
2
```

### 算法分析

由题意，6×5`的巧克力可以切出`6`块`2×2`的巧克力或者`2`块`3×3` 的巧克力：

![6×5](https://blog.fivk.cn/usr/uploads/2022/02/3294319497.png)

[album type="photos"]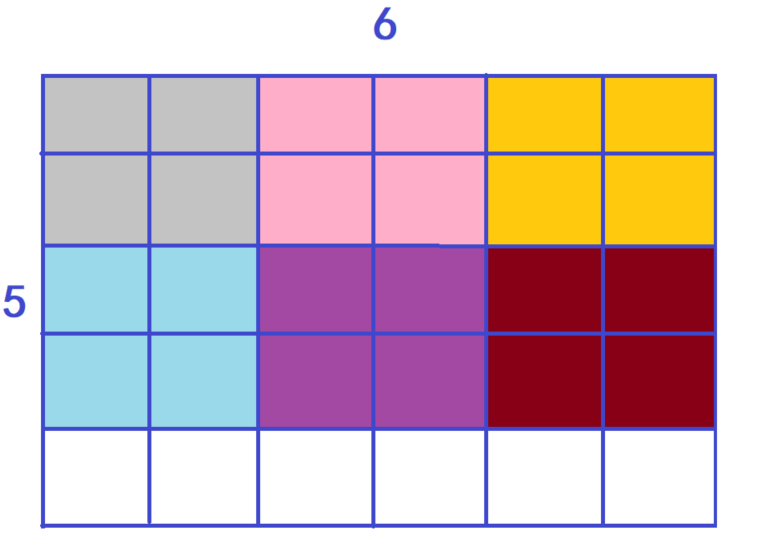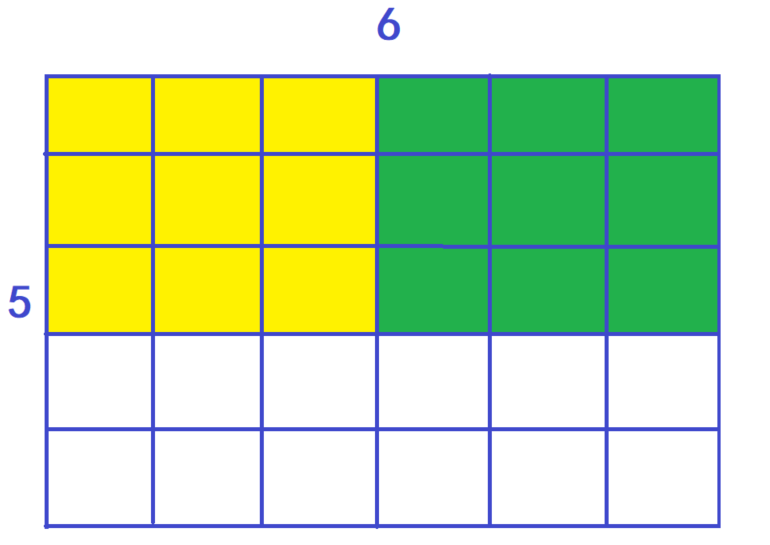

![6块2×2](https://blog.fivk.cn/usr/uploads/2022/02/161695195.png)

![2块3×3](https://blog.fivk.cn/usr/uploads/2022/02/3280149105.png)

[/album] </div>

#### 1.考虑是否能二分

很容易想到：边长越大，块数越小。

这里直接给出边长`x`对应块数`f(x)`的公式：$F(x)=\lfloor{\frac{W_i}{x}}\rfloor\times\lfloor\frac{H_i}{x}\rfloor$

对于我们的答案$X_0$，如果任意$X$满足$X{\leq}X_0$则$X$边长的小正方形一定能够切分，否则不能切分。

> 故满足二段性，可二分。

#### 2.判断二分的形式

二分有两个形式可参考以往笔记

<div class="inner-content" >
<p class="inser-title">【算法基础】二分查找算法模板</p>
<div class="inster-summary text-muted">
整数二分步骤：找一个区间[L, R]，使得答案一定在该区间中找一个判断条件，使得该判断条件具有二段性，并且答案一定...
</div>
</div>
</a>

</div>

</div>

根据我们想要得到大于等于第一个满足条件的值所以：

```cpp
if (F(Mid) >= K) L = Mid;
else R = Mid - 1;
```

因为我们写的是`L = Mid`所以我们的`Mid = L + R >> 1`。

### 参考程序

```cpp
#include <cstdio>
#include <iostream>
using namespace std;

const int N = 1e5 + 10;

int n, k;
int h[N], w[N];

bool check(int x) { // check函数代表解析中的F(x) 函数
    int res = 0;    // 表示一共可以分多少块
    for (int i = 0; i < n; i ++) {
        res += (h[i] / x) * (w[i] / x);
        if (res >= k) return true;
    }
    return false;
}

int main() {
    scanf("%d %d", &n, & k);
    for (int i = 0; i < n; i++) scanf("%d %d", &h[i], &w[i]);
  
    int l = 1, r = 1e5; // 答案保证大于1，不可能高于最大数据值
    while(l < r) {
        int mid = l + r + 1>> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
  
    printf("%d", r);
    return 0;
}
```

最后修改：2022 年 02 月 08 日