【数据结构】实验题

博主： Fivk
发布时间：2021 年 12 月 23 日
1330 次浏览
6635字数
分类：数据结构

# 7-1 单链表的创建及遍历 (30 分)

读入n值及n个整数，建立单链表并遍历输出。

### 输入格式:

读入n及n个整数。

### 输出格式:

输出n个整数，以空格分隔（最后一个数的后面没有空格）。

### 输入样例:

在这里给出一组输入。例如：

```in
2
10 5结尾无空行
```

### 输出样例:

在这里给出相应的输出。例如：

```out
10 5
```

```c
#include <stdio.h>
#include <stdlib.h>

typedef struct list {
	int data;
	struct list* next;
}*List;

int main()
{
	int n;
	List head = NULL, p = NULL, q = NULL;
	scanf("%d",&n);
	for (int i = 0; i < n; i++)
	{
		p = (List)malloc(sizeof(list));
		scanf("%d",&p->data);
		p->next = NULL;
		if (head == NULL)
		{
			head = p;
			q = p;
		} else {
			q -> next = p;
			q = q -> next;
		}
	}

for (List L = head; L != NULL; L = L -> next)
	{
		printf("%d",L -> data);
		if (L -> next != NULL) printf(" ");
	}

return 0;
} 
```

# 7-2 单链表基本操作 (5 分)

请编写程序实现单链表插入、删除结点等基本算法。给定一个单链表和一系列插入、删除结点的操作序列，输出实施上述操作后的链表。单链表数据域值为整数。

### 输入格式:

输入第1行为1个正整数n，表示当前单链表长度；第2行为n个空格间隔的整数，为该链表n个元素的数据域值。第3行为1个正整数m，表示对该链表施加的操作数量；接下来m行，每行表示一个操作，为2个或3个整数，格式为0 k d或1 k。0 k d表示在链表第k个结点后插入一个数据域值为d的结点，若k=0则表示表头插入。1 k表示删除链表中第k个结点，此时k不能为0。注：操作序列中若含有不合法的操作（如在长度为5的链表中删除第8个结点、删除第0个结点等），则忽略该操作。n和m不超过100000。

### 输出格式:

输出为一行整数，表示实施上述m个操作后的链表，每个整数后一个空格。输入数据保证结果链表不空。

### 输入样例:

```in
5
1 2 3 4 5
5
0 2 8
0 9 6
0 0 7
1 0 
1 6
```

### 输出样例:

```out
7 1 2 8 3 5 
```

```c
#include <stdio.h>
#include <stdlib.h>

typedef struct list {
	int data;
	struct list* next;
}*List;

void Insert(List &L, int k, int d)
{
	List p = (List)malloc(sizeof(struct list));
	p -> data = d;
	p -> next = NULL;
	if (k == 0)
	{
		p -> next = L;
		L = p;
		return;
	}
	List q = L;
	for (int i = 1; i < k; i++)
		q = q -> next;
	p -> next = q -> next;
	q -> next = p;
}

void Delete(List &L, int k)
{
	List q = L, p;
	for (int i = 1; i < k; i++) {
		p = q;
		q = q -> next;
	}

if (q == L) {
		L = L -> next;
	} else {
		p -> next = q -> next;
	}
	free(q);
}

int main()
{
	int n;
	List head = NULL, p = NULL, q = NULL;
	scanf("%d",&n);
	for (int i = 0; i < n; i++) {
		p = (List)malloc(sizeof(list));
		scanf("%d",&p->data);
		p->next = NULL;
		if (head == NULL) {
			head = p;
			q = p;
		} else {
			q -> next = p;
			q = q -> next;
		}
	}

//	for (List L = head; L != NULL; L = L -> next)
//	{
//		printf("%d",L -> data);
//		if (L -> next != NULL) printf(" ");
//	}
//	printf("\n\n\n");
	int m;
	scanf("%d",&m);
	int t,k,d;

while(m--) 
	{
		scanf("%d",&t);
		switch(t) {
			case 0:
				scanf("%d %d",&k,&d);
				if (k <= n) {
					Insert(head,k,d);
					n++;
				}
				break;
			case 1:
				scanf("%d",&k);
				if (k >= 1 && k <= n) {
					Delete(head, k);
					n--;
				}
				break;
		}
	}

for (List L = head; L != NULL; L = L -> next)
		printf("%d ",L -> data);
    printf("\n");

return 0;
} 
```

# 7-3 求解迷宫从入口到出口的路径 (15 分)

求解迷宫从入口到出口的路径。输入一个迷宫，求从入口通向出口的可行路径。为简化问题，迷宫用二维数组 int maze[10][10]来存储障碍物的分布，假设迷宫的横向和纵向尺寸的大小是一样的，并由程序运行读入, 若读入迷宫大小的值是n（3<n<=10），则该迷宫横向或纵向尺寸都是n，规定迷宫最外面的一圈是障碍物，迷宫的入口是maze[1][1]，出口是maze[n-2][n-2], 若maze[i][j] = 1代表该位置是障碍物，若maze[i][j] = 0代表该位置是可以行走的空位（0<=i<=n-1, 0<=j<=n-1）。求从入口maze[1][1]到出口maze[n-2][n-2]可以走通的路径。要求迷宫中只允许在水平或上下四个方向的空位上行走，走过的位置不能重复走，规定必须按向右、向下、向左、向上的顺序向前搜索试探。 如下这样一个迷宫：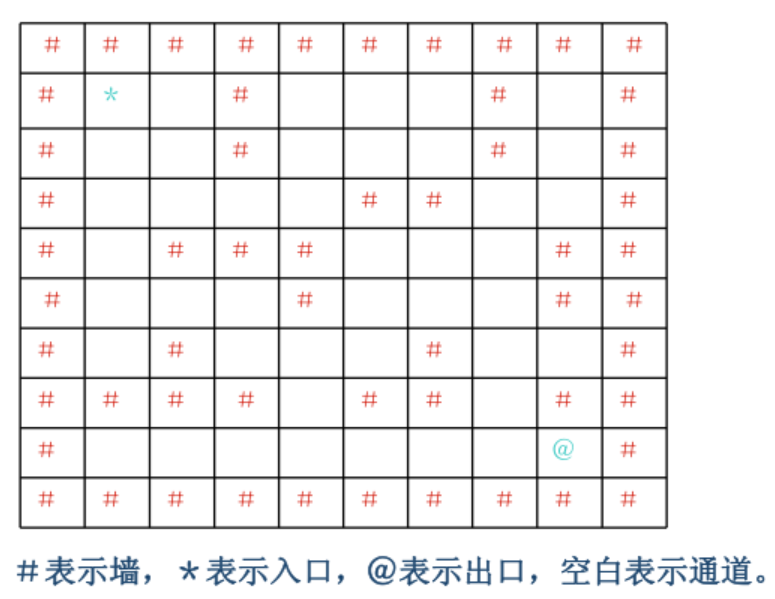

![dddd.png](https://blog.fivk.cn/usr/uploads/2021/12/3871161185.png)

对应的二维数组表示： int maze[10][10]={ {1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,0,0,1,1,0,0,1}, {1,0,1,1,1,0,0,0,1,1}, {1,0,0,0,1,0,0,0,1,1}, {1,0,1,0,0,0,1,0,0,1}, {1,1,1,1,0,1,1,0,1,1}, {1,0,0,0,0,0,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1}};

### 输入格式:

输入迷宫大小的整数n, 以及n行和n列的二维数组（数组元素1代表障碍物，0代表空位）。

### 输出格式:

依次输出从入口到出口可行路径每个位置的行列下标（i,j），每个位置间用“,”分隔。若没有通路，输出：NO。

### 输入样例1:

```in
4
1 1 1 1
1 0 1 1
1 0 0 1
1 1 1 1
```

### 输出样例1:

```out
(1,1)(2,1)(2,2)
```

### 输入样例2:

```in
10
1 1 1 1 1 1 1 1 1 1
1 0 0 1 0 0 0 1 0 1
1 0 0 1 0 0 0 1 0 1
1 0 0 0 0 1 1 0 0 1
1 0 1 1 1 0 0 0 0 1
1 0 0 0 1 0 0 0 0 1
1 0 1 0 0 0 1 0 0 1
1 0 1 1 1 0 1 1 0 1
1 1 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1
```

### 输出样例2:

```out
(1,1)(1,2)(2,2)(3,2)(3,1)(4,1)(5,1)(5,2)(5,3)(6,3)(6,4)(6,5)(7,5)(8,5)(8,6)(8,7)(8,8)
```

```cpp
#include <bits/stdc++.h>
using namespace std;
#define N 10

bool flag = false;
int n;
int a[N][N];

const int di[] = {0,1,0,-1};
const int dj[] = {1,0,-1,0};

struct Node {
	int i;
	int j;
};

vector<Node> p;
Node t;
void Print()
{
	for (Node node:p)
		printf("(%d,%d)",node.i, node.j);
}

void dfs(int x, int y)
{

if (flag) return;
	if (x == n - 2 && y == n - 2)
	{
		flag = true;
		Print();
		return;
	}

for (int i = 0; i < 4; i++)
	{
		int xi = x + di[i];
		int yj = y + dj[i];
		t.i = xi;
		t.j = yj;
		if (xi > 0 && xi < n && yj > 0 && yj < n && !a[xi][yj])
		{
			p.push_back(t);
			a[xi][yj] = 1;
			dfs(xi,yj);
			p.pop_back();
			a[xi][yj] = 0;
		}
	}

}

int main()
{
	cin >> n;

for (int i = 0; i < n; i ++)
		for (int j = 0; j < n; j++)
			scanf("%d",&a[i][j]);
	t.i = 1;
	t.j = 1;
	p.push_back(t);
	dfs(1,1);
	if (!flag) printf("NO");
}
```

# 7-4 求解迷宫从入口到出口的一条最短路径 (15 分)

求解迷宫从入口到出口的一条最短路径。输入一个迷宫，求从入口通向出口的一条可行最短路径。为简化问题，迷宫用二维数组 int maze[10][10]来存储障碍物的分布，假设迷宫的横向和纵向尺寸的大小是一样的，并由程序运行读入, 若读入迷宫大小的值是n（3<n<=10），则该迷宫横向或纵向尺寸都是n，规定迷宫最外面的一圈是障碍物，迷宫的入口是maze[1][1]，出口是maze[n-2][n-2], 若maze[i][j] = 1代表该位置是障碍物，若maze[i][j] = 0代表该位置是可以行走的空位（0<=i<=n-1, 0<=j<=n-1）。求从入口maze[1][1]到出口maze[n-2][n-2]可以走通的路径。要求迷宫中只允许在水平或上下四个方向的空位上行走，走过的位置不能重复走，规定必须按向右、向下、向左、向上的顺序向前搜索试探，输出先到达出口的最短路径。 如下这样一个迷宫：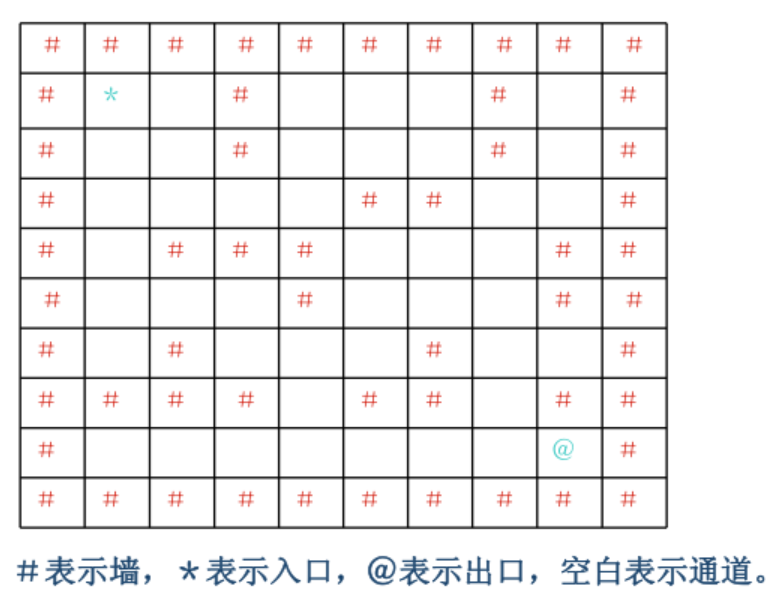

![dddd.png](https://blog.fivk.cn/usr/uploads/2021/12/2795296137.png)

### 输入格式:

输入迷宫大小的整数n, 以及n行和n列的二维数组（数组元素1代表障碍物，0代表空位）。

### 输出格式:

输出按规定搜索试探顺序先到达出口的首条最短路径，依次输出从入口到出口可行最短路径每个位置的行列下标（i,j），每个位置间用“,”分隔。若没有通路，输出：NO。

### 输入样例1:

```in
4
1 1 1 1
1 0 1 1
1 0 0 1
1 1 1 1
```

### 输出样例1:

```out
(1,1)(2,1)(2,2)
```

### 输入样例2:

### 输出样例2:

```out
(1,1)(2,1)(3,1)(4,1)(5,1)(5,2)(5,3)(6,3)(6,4)(6,5)(7,5)(8,5)(8,6)(8,7)(8,8)
```

```c
#include <stdio.h>

const int di[] = {0,1,0,-1};
const int dj[] = {1,0,-1,0};

int n, head, tail, x, y, a[101], b[101], pre[101], map[12][12];

int f;

void print(int d)
{
	if (pre[d] != 0) print(pre[d]);
		printf("(%d,%d)",a[d],b[d]); 
}

int main()
{
	int i, j;
	scanf("%d",&n);
	for (i = 0; i < n; i++)
		for (j = 0; j < n; j++)
			scanf("%d",&map[i][j]);

head = 0;
	tail = 1;

f = 0;
	map[1][1] = 1;
	a[tail] = 1;
	b[tail] = 1;
	pre[tail] = 0;

while (head != tail)
	{
		head++;
		for (i = 0; i < 4; i++)
		{
			x = a[head] + di[i];
			y = b[head] + dj[i];

if ((x > 0) && (x < n) && (y > 0) && (y < n) && map[x][y] == 0)
			{
				tail++;
				a[tail] = x;
				b[tail] = y;
				pre[tail] = head;
				map[x][y] = 1;
				if ((x == n - 2) && (y == n - 2))
				{
					f = 1;
					print(tail);
					break;
				}
			}
		}
		if (f) break;
	} 
	 
	if (!f) puts("NO");
	return 0;
}
```

# 7-5 公路村村通 (30 分)

现有村落间道路的统计数据表中，列出了有可能建设成标准公路的若干条道路的成本，求使每个村落都有公路连通所需要的最低成本。

### 输入格式:

输入数据包括城镇数目正整数**N**（**≤****1000**）和候选道路数目**M**（**≤****3****N**）；随后的**M**行对应**M**条道路，每行给出3个正整数，分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见，城镇从1到**N**编号。

### 输出格式:

输出村村通需要的最低成本。如果输入数据不足以保证畅通，则输出**−****1**，表示需要建设更多公路。

### 输入样例:

```in
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
```

### 输出样例:

```out
12
```

```cpp
#include <stdio.h>
#include <string.h>
#define N 1001

const int M = 1000;

int u,v,Min[N], mst,G[N][N];
int b[N];

int main()
{
	memset(Min,0x7f,sizeof(Min));
	memset(G,0x7f,sizeof(G));
	int n,m;
	scanf("%d %d",&n, &m);
	for (int i = 1; i <= m; i++)
	{
		int x,y,z;
		scanf("%d %d %d",&x,&y,&z);
		G[x][y] = G[y][x] = z;
	}

Min[1] = 0;
	mst = 0;

for (int i = 1; i <= n; i++)
	{
		int u = 0, min = M;

for (int j = 1; j <= n; j++)
			if (!b[j] && Min[j] < min)
			{
				min = Min[j];
				u = j;
			}

if (u == 0)
		{
			printf("-1");
			return 0;
		}

b[u] = 1;
		mst += Min[u]; 
		for (int j = 1; j <= n; j++)
			if (!b[j] && Min[j] > G[u][j])
				Min[j] = G[u][j];
	}
	printf("%d",mst);
	return 0;
}
```

# 7-6 最短路径之Dijkstra (10 分)

本题目要求通过读入无向网的边的信息（省略了各顶点的信息，仅用顶点编号来表示），构造图，并利用Dijkstra算法，求出指定源点到其它各点的最短路径。

### 输入样例:

第一行，两个整数，顶点数vN和边数eN。 以后若干行，是相关边的信息，无向图的边是对称的，只输入一半的边（小编号到大编号的，间以空格），最后两行各一个整数，前一个指定源点，后一个指定的查询的终到点。 （注意，示例中34条边，只输入了17条边的信息）

```in
10 34
0 1 2
0 3 5
1 2 5
1 3 2
2 4 8
2 5 4
3 5 4
3 6 2
4 7 5
4 5 2
5 6 3
5 7 9
5 8 7
6 8 7
7 8 3
7 9 4
8 9 8
0
8
```

### 输出样例:

在一行中输出从源点到指定终点的短路径及代价，注意：所有符号均为西文符号。

```out
0-->1-->3-->6-->8:13
```

```c
// #include <stdio.h>
// #include <string.h>

// void print(int pre[], int k, int t)
// {
// 	if (k == -1) return;
// 	print(pre,pre[k],t);
// 	printf("%d",k);
// 	if (k != t) printf("-->");
// }

// int main()
// {
// 	int v,e;
// 	scanf("%d %d",&v, &e);
//     e/=2;
// 	int w[1001][1001], dis[1001],pre[1001];
// 	int b[1001] = {0};
// 	memset(w,0x7f,sizeof(w));
// 	memset(dis,0x7f,sizeof(dis));
// 	memset(pre,0x7f,sizeof(pre));

// 	for (int i = 0; i < e; i++)
// 	{
// 		int x, y, z;
// 		scanf("%d %d %d",&x, &y ,&z);
// 		w[x][y] = w[y][x] = z;
// 	}

// 	int s,t;
// 	scanf("%d %d",&s, &t);

// 	b[s] = 1;

// 	for (int i = 0; i < v; i++)
// 	{
// 		dis[i] = w[s][i];
// 		pre[i] = s;
// 	}
// 	dis[s] = 0;
// 	for (int i = 0; i < v - 1; i++)
// 	{
// 		int k = -1, min = 0x7fffffff;
// 		for (int j = 0; j < v; j++)
// 		{
// 			if (!b[j] && dis[j] < min)
// 			{
// 				k = j;
// 				min = dis[j];
// 			}
// 		}

// 		if (k == -1) break;
// 		b[k] = 1;
// 		for (int j = 0; j < v; j++)
// 			if (dis[j] > dis[k] + w[k][j])
// 			{
// 				dis[j] = dis[k] + w[k][j];
// 				pre[j] = k;
// 			}
// 	}
// 	pre[s] = -1;
// 	print(pre,t,t);
// 	printf(":%d",dis[t]);
// 	return 0;
// }

// 不会了，搜的
#include<iostream>
#include<vector>
using namespace std;

#define INF 10001

struct Node{
	int v,l;//一条路的尾结点，该路的长度 
};

int n,e,start,stop;
vector<Node> v[1001];
//使用二维动态数组 ,其实二维动态数组和普通数组的唯一区别就在于定义不一样，其他的使用方法和意义都是一样的 ，所以千万不要觉得麻烦
int dist[1001];
int path[1001];
int visit[1001];

void Dijkstra(int start){
	fill(dist,dist + 1001,INF);
	dist[start] = 0;
	for(int i = 0;i < n;i ++){
		int u = -1,minx = INF;
		for(int j = 0;j < n;j ++){
			if(visit[j] == 0 && dist[j] < minx){
				minx = dist[j];
				u = j;
			}
		}
		if(u == -1) break;
		visit[u] = 1;
		for (int j = 0; j < v[u].size(); j++) {
            int x = v[u][j].v;
            if (visit[x] == 0 && dist[u] + v[u][j].l < dist[x]) {
                dist[x] = dist[u] + v[u][j].l;
                path[x] = u;
            }
        }
	}
}

int main(){
	cin >> n >> e;
    for (int i = 0; i < e / 2; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        //这两行就相当于用二维数组的edge[a][b] = edge[b][a] = c;但是很多情况下用二维数组都会运行超时，要不然就内存超限 
        v[a].push_back(Node{b, c});
        v[b].push_back(Node{a, c});
    }
    cin >> start >> stop;
    if (start == stop) {//如果起点和终点是同一个结点 
        printf("%d-->%d:0",start,start);
        return 0;
    }
    Dijkstra(start);
    vector<int> ve;
    int x = stop;
    while (x != start) {
        ve.push_back(x);
        x = path[x];
    }
    cout << start;
    for (int i = ve.size() - 1; i >= 0; i--)
        cout << "-->" << ve[i];//动态数组的输出也不一定需要迭代器 
    cout << ":" << dist[stop];
}

```

# 7-7 地下迷宫探索 (30 分)

地道战是在抗日战争时期，在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事，如下图所示。

![](https://images.ptausercontent.com/52)

我们在回顾前辈们艰苦卓绝的战争生活的同时，真心钦佩他们的聪明才智。在现在和平发展的年代，对多数人来说，探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。

假设有一个地下通道迷宫，它的通道都是直的，而通道所有交叉点（包括通道的端点）上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点？

![](https://images.ptausercontent.com/53)

### 输入格式:

输入第一行给出三个正整数，分别表示地下迷宫的节点数**N**（**1****<****N****≤****1000**，表示通道所有交叉点和端点）、边数**M**（**≤****3000**，表示通道数）和探索起始节点编号**S**（节点从1到**N**编号）。随后的**M**行对应**M**条边（通道），每行给出一对正整数，分别是该条边直接连通的两个节点的编号。

### 输出格式:

若可以点亮所有节点的灯，则输出从**S**开始并以**S**结束的包含所有节点的序列，序列中相邻的节点一定有边（通道）；否则虽然不能点亮所有节点的灯，但还是输出点亮部分灯的节点序列，最后输出0，此时表示迷宫不是连通图。

由于深度优先遍历的节点序列是不唯一的，为了使得输出具有唯一的结果，我们约定以节点小编号优先的次序访问（点灯）。在点亮所有可以点亮的灯后，以原路返回的方式回到起点。

### 输入样例1:

```in
6 8 1
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5
```

### 输出样例1:

```out
1 2 3 4 5 6 5 4 3 2 1
```

### 输入样例2:

```
6 6 6
1 2
1 3
2 3
5 4
6 5
6 4
```

### 输出样例2:

```
6 4 5 4 6 0
```

```c
// #include <stdio.h>
// #include <string.h>
// int a[1001][1001];
// int b[1001];
// int count;
// int c[1001], t;
// int n,m,s;
// int TEST = 0;

// void print()
// {
// 	TEST  = 1;
//     int test = 0;
// 	for (int i = 0; i < t; i++)
// 	{
// 		printf("%d", c[i]);
// 		if(i < t - 1) printf(" ");
// 	}
//     if (t > 1)
// 	for (int i = t - 2; i >= 0; i--)
// 	{
// 		printf(" %d",c[i]);
// 	}
// 	if (t < n - 1) printf(" 0");
// 	printf("\n");
// }

// void dfs(int k)
// {
// 	if (TEST) return;
// 	int test = 0;
// 	for (int i = 1; i <= n; i++)
// 	{
// 		if (!b[i] && a[i][k] )
// 		{
// 			test = 1;
// 			c[t] = i;
// 			b[i] = 1;
// 			a[i][k] = a[k][i] = 0;
// 			t++;
// 			count--;
// 			dfs(i);
// 			b[i] = 0;
// 			a[i][k] = a[k][i] = 1;
// 			t--;
// 		}
// 	}
// 	if (!test) print();
// }

// void fivk()
// {
//     memset(a,0,sizeof(a));
//     memset(b,0,sizeof(b));
//     memset(a,0,sizeof(a));
//     t = 0;
// 	count = n;
// 	TEST = 0;
// 	for (int i = 1; i <= m; i++)
// 	{
// 		int x, y;
// 		scanf("%d %d", &x, &y);
// 		a[x][y] = a[y][x] = 1;
// 	}
// 	b[s] = 1;
// 	c[t] = s;
// 	t++;
// 	dfs(s);
// }

// int main()
// {
//     while(~scanf("%d %d %d",&n, &m, &s))
//     {
//         fivk();
//     }
// 	return 0;
// }

// 只对了两个测试点

// 搜的
#include <iostream>
#include <cstdlib>
#include <string>
using namespace std;
int N, M, S, v = 1;
int G[1001][1001];
int visit[1001];
int flag = 0;
void ULE(int a)
{
	if (flag)
		cout << " ";
	flag++;
	cout << a;
	for (int i = 1; i <= N; i++)
	{
		if (!visit[i] && G[a][i])
		{
			visit[i] = 1;
			v++;
			ULE(i);
			cout << " " << a;
		}
	}
}
void CreatG()
{
	int a, b;
	for (int i = 0; i < M; i++)
	{
		cin >> a >> b;
		G[a][b] = G[b][a] = 1;
	}
}
int main()
{
	cin >> N >> M >> S;
	CreatG();
	visit[S] = 1;
	ULE(S);
	if (v < N)
		cout << " 0";
}

```

# 7-8 最短路径 (20 分)

给定一个有N个顶点和E条边的无向图，顶点从0到N−1编号。请判断给定的两个顶点之间是否有路径存在。如果存在，给出最短路径长度。 这里定义顶点到自身的最短路径长度为0。 进行搜索时，假设我们总是从编号最小的顶点出发，按编号递增的顺序访问邻接点。

### 输入格式:

输入第1行给出2个整数N(0<N≤10)和E，分别是图的顶点数和边数。 随后E行，每行给出一条边的两个顶点。每行中的数字之间用1空格分隔。 最后一行给出两个顶点编号i，j（0≤i,j<N）,i和j之间用空格分隔。

### 输出格式:

如果i和j之间存在路径，则输出"The length of the shortest path between i and j is X."，X为最短路径长度， 否则输出"There is no path between i and j."。

### 输入样例1:

```in
7 6
0 1
2 3
1 4
0 2
1 3
5 6
0 3
```

### 输出样例1:

```out
The length of the shortest path between 0 and 3 is 2.
```

### 输入样例2:

```in
7 6
0 1
2 3
1 4
0 2
1 3
5 6
0 6
```

### 输出样例2:

```out
There is no path between 0 and 6.
```

```c
// #include <stdio.h>
// #include <string.h>
// int w[12][12];
// int dis[12];
// int n,e;
// int b[12];
// int test = 0;

// int main()
// {
// 	scanf("%d %d",&n, &e);
// 	memset(w,1,sizeof(w));
// 	memset(dis,1,sizeof(dis));
// 	for (int i = 0; i < e; i++)
// 	{
// 		int x,y;
// 		scanf("%d %d",&x, &y);
// 		w[x][y] = w[y][x] = 1;
// 	}

// 	for (int i = 0; i < n; i++)
// 		w[i][i] = 0;

// 	int s,t;
// 	scanf("%d %d",&s, &t);
//     if (s == t)
//     {
//         printf("The length of the shortest path between %d and %d is 0.\n",s,s);
//         return 0;
//     }
// 	dis[s] = 0;
// 	b[s] = 1;

// 	for (int i = 0; i < n; i++)
// 		dis[i] = w[s][i];

// 	for (int i = 0; i < n - 1; i++)
// 	{
// 		int k = -1, min = 10000;
// 		for (int j = 0; j < n; j++)
// 		{
// 			if (!b[j] && dis[j] < min)
// 			{
// 				min = dis[j];
// 				k = j;
// 			}
// 		}

// 		if (k == -1)
// 		{
// 			test = 1;
// 			break;
// 		}

// 		b[k] = 1;

// 		for (int j = 0; j < n; j++)
// 		{
// 			if (dis[j] > dis[k] + w[k][j])
// 			{
// 				dis[j] = dis[k] + w[k][j];
// 			}
// 		}
// 	}

// 	if (test)
// 	{
// 		printf("There is no path between %d and %d.\n",s,t);
// 	} else {
// 		printf("The length of the shortest path between %d and %d is %d.\n",s,t,dis[t]);
// 	} 
// 	return 0;
// }

// 迪杰斯特拉错了一个点，试试floyde

// #include <stdio.h>
// #include <string.h>
// int w[12][12];
// int n,m;
// int main()
// {
//     scanf("%d %d",&n,&m);
//     memset(w,1,sizeof(w));
//     for (int i = 0; i < m; i++)
//     {
//         int x,y;
//         scanf("%d %d",&x,&y);
//         w[x][y] = w[y][x] = 1;
//     }
//     int s,t;
//     scanf("%d %d",&s,&t);
//     for (int k = 0; k < n; k++)
//         for (int i = 0; i < n; i++)
//             for (int j = 0; j < n; j++)
//                 if (i != j && j != k && i != k)
//                     if (w[i][j] > w[i][k] + w[k][j])
//                         w[i][j] = w[i][k] + w[k][j];
//     int dis = w[s][t];
//     if (dis < 1000)
//         printf("The length of the shortest path between %d and %d is %d.\n",s,t,dis);
//     else
//         printf("There is no path between %d and %d.\n",s,t);
//     return 0;
// }

// floyde也错了一个点，但是分数高一点

#include<bits/stdc++.h>
using namespace std;
int minstep = 0x7fffffff;
int n, e;
vector<int> v[1005];
int book[1005];
int flag = 0;
void dfs(int a, int b,int step) {
	if (a == b) {
		flag = 1;
		if (step < minstep)
			minstep = step;
		return;
	}
	int len = v[a].size();
	for (int i = 0;i < len;i++) {
		if (book[v[a][i]] == 0) {
			book[v[a][i]] = 1;
			if (step + 1 < minstep)
				dfs(v[a][i], b, step + 1);
			book[v[a][i]] = 0;
		}
	}
}
int main() {
	cin >> n >> e;
	for (int i = 1;i <= e;i++) {
		int a, b;
		cin >> a >> b;
		v[a].push_back(b);
		v[b].push_back(a);
	}
	for (int i = 0;i < n;i++)
		sort(v[i].begin(), v[i].end());
	int a, b;
	cin >> a >> b;
	dfs(a, b,0);
	if (flag)
		printf("The length of the shortest path between %d and %d is %d.", a, b, minstep);
	else
		printf("There is no path between %d and %d.", a, b);
}

```

# 7-9 二叉树的创建与遍历 (5 分)

通过带空指针信息的先根序列（亦称先序序列）创建二叉树，并进行先根（先序）、中根（中序）、后根（后序）遍历。二叉树结点数据域值为不等于0的整数（可能是正数也可能是负数），空指针用0表示，例如1 5 8 0 0 0 6 0 0表示如下图的二叉树。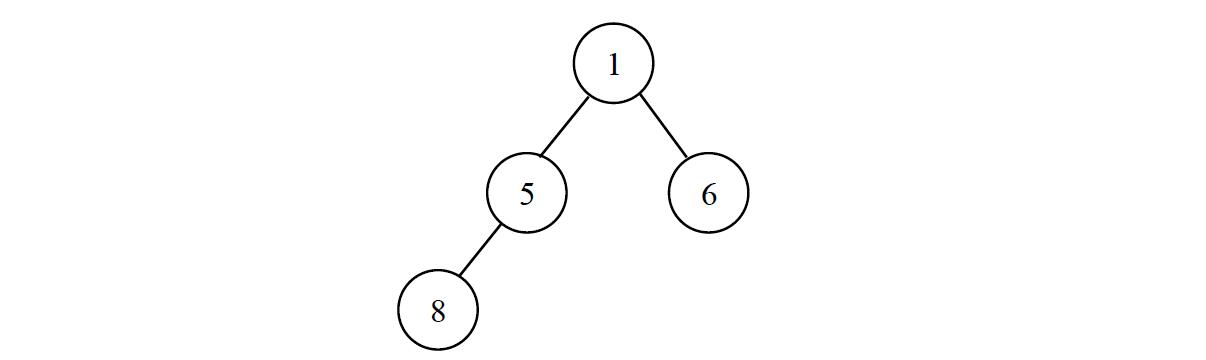

![PA567.jpg](https://blog.fivk.cn/usr/uploads/2021/12/3328504184.jpg)

### 输入格式:

输入为一组用空格间隔的整数，表示带空指针信息的二叉树先根序列。其中空指针信息用0表示。二叉树结点个数不超过150000，高度不超过6000。输入数据保证二叉树各结点数据值互不相等。

### 输出格式:

输出为3行整数，每个整数后一个空格。第1行为该二叉树的先根序列，第2行为中根序列，第3行为后根序列。

### 输入样例:

```in
1 5 8 0 0 0 6 0 0
```

### 输出样例:

```out
1 5 8 6 
8 5 1 6 
8 5 6 1 
```

```c
#include <stdio.h>
#include <stdlib.h>

typedef struct tree {
	int x;
	struct tree *lchild;
	struct tree *rchild;
}* Tree;

Tree insert(Tree root)
{
	int x;
	scanf("%d", &x);
	if (x != 0)
	{
		root = (Tree)malloc(sizeof(struct tree));
		root -> x = x;
		root -> lchild = root -> rchild = NULL;
		root -> lchild = insert(root -> lchild);
		root -> rchild = insert(root -> rchild);
	}
	return root;
}

void print_pre(Tree root)
{
	if (root == NULL)
		return;

printf("%d ",root -> x);
	print_pre(root->lchild);
	print_pre(root->rchild);
}

void print_mid(Tree root)
{
	if (root == NULL)
		return;

print_mid(root->lchild);
	printf("%d ",root -> x);
	print_mid(root->rchild);
}

void print_tail(Tree root)
{
	if (root == NULL)
		return;

print_tail(root->lchild);
	print_tail(root->rchild);
	printf("%d ",root -> x);
}

int main()
{
	Tree root = NULL;
	root = insert(root);
	print_pre(root);
    printf("\n");
	print_mid(root);
    printf("\n");
	print_tail(root);
    printf("\n");
	return 0;
 } 
```

# 7-10 构造哈夫曼树 (20 分)

输入一些单词及其出现的频度，构造一棵哈夫曼树，输出哈夫曼编码的平均码长。

### 输入格式:

输入N，表示有N个单词，以下N行，每一行表示一个单词及其频度。

### 输出格式:

平均码长用浮点数类型表示，保留小数点后5位。

### 输入样例:

在这里给出一组输入。例如：

```in
11
The 1192
of 677
a 541
to 518
and 462
that 242
he 195
is 190
for 157
His 138
are 124
```

### 输出样例:

在这里给出相应的输出。例如：

```out
3.10437
```

# 7-11 快速排序 (10 分)

给定包含n个元素的整型数组a[1],a[2],...,a[n]，利用快速排序算法对其进行递增排序，请输出排序过程，即每次Partition之后的数组。每次选择所处理的子数组的第一个元素作为基准元素。

### 输入格式:

输入为两行，第一行为一个整数n（1<n≤1000），表示数组长度。第二行为n个空格间隔的整数，表示待排序的数组。

### 输出格式:

输出为若干行，每行依次输出Partition后的数组，每个元素后一个空格。

### 输入样例:

```in
5
4 5 3 2 1
```

### 输出样例:

```out
2 1 3 4 5 
1 2 3 4 5 
1 2 3 4 5 
```

```c
#include <stdio.h>
int n;
void sort(int a[], int l, int r)
{
	if (l >= r) return;
	int i = l,j = r;
	int key = a[i];
	int temp;
	while(i < j)
	{
		while(i < j && a[j] > key) j--;
		while(i < j && a[i] <= key) i++;
		if (i < j) {
			temp = a[i];
			a[i] = a[j];
			a[j] = temp;
		}
	}
	temp = a[l];
	a[l] = a[i];
	a[i] = temp;
	int flag = 1;
	for (int k = 0; k < n; k++) 
	{
		printf("%d ",a[k]);
		if (k != 0 && a[k-1] > a[k])
			flag = 0;	// 这样可以减少无效的排序次数
	}
	printf("\n");
	if (flag) return;
	sort(a,l,j-1);
	sort(a,j+1,r);
}

int main()
{
	int a[1002];
	scanf("%d",&n);
	for (int i = 0; i < n; i++)
		scanf("%d",&a[i]);
	sort(a,0,n-1);
	for (int i = 0; i < n; i++)
		printf("%d ", a[i]);
    printf("\n");
	return 0;
} 
```

# 7-12 堆排序 (10 分)

对n个数，要求用堆排序（最大堆）对其进行排序。

### 输入格式:

第一行一个n（n<1000）。第二行给出n个数。

### 输出格式:

输出n行，每行n个数。第一行表示将n个数(将n个数看成一棵树)变成最大堆后的结果，第二行表示将上次结果的根节点交换到现有节点的最后一个节点（然后将除最后一个节点的数看成一颗树），然后将该剩余节点树从新变成最大堆后的结果输出（包括交换到最后的节点），依次类推。

### 输入样例:

```in
6
7 1 6 4 3 5
```

### 输出样例:

```out
7 4 6 1 3 5 
6 4 5 1 3 7 
5 4 3 1 6 7 
4 1 3 5 6 7 
3 1 4 5 6 7 
1 3 4 5 6 7 
```

```cpp
// 不会，，
//
//  main.cpp
//  Cpp_Homework
//
//  Created by 傅鳕鱼 on 2021/6/16.
//

#include <iostream>
#include <algorithm>
using namespace std;

void HeapAdjust(int *a,int i,int size)  //调整堆
{
    int lchild=2*i;       //i的左孩子节点序号
    int rchild=2*i+1;     //i的右孩子节点序号
    int max=i;            //临时变量
    if(i<=size/2)          //如果i不是叶节点就不用进行调整
    {
        if(lchild<=size&&a[lchild]>a[max])
        {
            max=lchild;
        }
        if(rchild<=size&&a[rchild]>a[max])
        {
            max=rchild;
        }
        if(max!=i)
        {
            swap(a[i],a[max]);
            HeapAdjust(a,max,size);    //避免调整之后以max为父节点的子树不是堆
        }

}

void BuildHeap(int *a,int size)    //建立堆
{
    int i;
    for(i=size/2;i>=1;i--)    //非叶节点最大序号值为size/2
    {
        HeapAdjust(a,i,size);

}
    for(int c=1;c<=size;c++)
        cout<<a[c]<<" ";
    cout<<endl;
}

void HeapSort(int *a,int size)    //堆排序
{
    int i;
    BuildHeap(a,size);
    for(i=size;i>1;i--)
    {
        //cout<<a[1]<<" ";
        swap(a[1],a[i]);           //交换堆顶和最后一个元素，即每次将剩余元素中的最大者放到最后面
          //BuildHeap(a,i-1);        //将余下元素重新建立为大顶堆
        HeapAdjust(a,1,i-1);      //重新调整堆顶节点成为大顶堆
        for(int c=1;c<=size;c++)
            cout<<a[c]<<" ";
        cout<<endl;

}
}

int main(int argc, char *argv[])
{
    int a[100];
    int size;
    while(scanf("%d",&size)==1&&size>0)
    {
        int i;
        for(i=1;i<=size;i++)
            cin>>a[i];
        HeapSort(a,size);
//        for(i=1;i<=size;i++)
//            cout<<a[i]<<" ";
//        cout<<endl;
    }
    return 0;
}
```

# 7-13 二分查找 (20 分)

输入n值(1<=n<=1000)、n个非降序排列的整数以及要查找的数x，使用**二分查找算法** 查找x，输出x所在的下标（0~n-1）及比较次数。若x不存在，输出-1和比较次数。

### 输入格式:

输入共三行： 第一行是n值； 第二行是n个整数； 第三行是x值。

### 输出格式:

输出x所在的下标（0~n-1）及比较次数。若x不存在，输出-1和比较次数。

### 输入样例:

```in
4
1 2 3 4
```

### 输出样例:

```out
0
2
```

```c
#include <stdio.h>
int main()
{
	int a[1001];
	int n,x;
	scanf("%d",&n);
	for (int i = 0; i < n; i++)
		scanf("%d",&a[i]);
	scanf("%d",&x);
	int l = 0, r = n - 1,mid;
	int count = 0;
	while(l <= r)
	{
		mid = l + r >> 1;
		count++;
		if (a[mid] == x) {
			printf("%d\n",mid);
			printf("%d",count);
			return 0;
		} else if (a[mid] > x) {
			r = mid - 1;
		} else {
			l = mid + 1;
		}
	}
	printf("-1\n");
	printf("%d",count);
	return 0;
}
```

# 7-14 统计成绩2 (10 分)

统计学生成绩(数据规模大，高效输入和高效算法，主要是卡时) 本题要求编写程序读入N个学生的百分制成绩，统计五分制成绩的分布。百分制成绩到五分制成绩的转换规则： •大于等于90分为A； •小于90且大于等于80为B； •小于80且大于等于70为C； •小于70且大于等于60为D； •小于60为E。

### 输入格式:

输入在第一行中给出一个正整数N（≤6000000），即学生人数；第二行中给出N个学生的百分制成绩（非负整数），其间以空格分隔。

### 输出格式:

在一行中输出A、B、C、D、E对应的五分制成绩的人数分布，数字间以空格分隔，行末不得有多余空格。

### 输入样例:

在这里给出一组输入。例如：

```in
7
77 54 92 73 60 65 69
```

### 输出样例:

在这里给出相应的输出。例如：

```out
1 0 2 3 1
```

# 7-15 建立二叉搜索树并查找父结点 (48 分)

按输入顺序建立二叉搜索树，并搜索某一结点，输出其父结点。

### 输入格式:

输入有三行： 第一行是n值，表示有n个结点； 第二行有n个整数，分别代表n个结点的数据值； 第三行是x，表示要搜索值为x的结点的父结点。

### 输出格式:

输出值为x的结点的父结点的值。 若值为x的结点不存在，则输出：It does not exist. 若值为x的结点是根结点，则输出：It doesn't have parent.

### 输入样例:

```in
2
20
30
20
```

### 输出样例:

```out
It doesn't have parent.
```

###输入样例：

```in
2
20
30
30
```

### 输出样例:

```out
20
```

最后修改：2021 年 12 月 23 日

如果觉得我的文章对你有用，请随意赞赏

【数据结构】实验题

Fivk • 2021 年 12 月 23 日

# 7-1 单链表的创建及遍历 (30 分)

读入n值及n个整数，建立单链表并遍历输出。

### 输入格式:

读入n及n个整数。

### 输出格式:

输出n个整数，以空格分隔（最后一个数的后面没有空格）。

### 输入样例:

在这里给出一组输入。例如：

```in
2
10 5结尾无空行
```

### 输出样例:

在这里给出相应的输出。例如：

```out
10 5
```

```c
#include <stdio.h>
#include <stdlib.h>

typedef struct list {
	int data;
	struct list* next;
}*List;

for (List L = head; L != NULL; L = L -> next)
	{
		printf("%d",L -> data);
		if (L -> next != NULL) printf(" ");
	}

return 0;
} 
```

# 7-2 单链表基本操作 (5 分)

### 输入格式:

### 输出格式:

输出为一行整数，表示实施上述m个操作后的链表，每个整数后一个空格。输入数据保证结果链表不空。

### 输入样例:

```in
5
1 2 3 4 5
5
0 2 8
0 9 6
0 0 7
1 0 
1 6
```

### 输出样例:

```out
7 1 2 8 3 5 
```

```c
#include <stdio.h>
#include <stdlib.h>

typedef struct list {
	int data;
	struct list* next;
}*List;

void Delete(List &L, int k)
{
	List q = L, p;
	for (int i = 1; i < k; i++) {
		p = q;
		q = q -> next;
	}

if (q == L) {
		L = L -> next;
	} else {
		p -> next = q -> next;
	}
	free(q);
}

int main()
{
	int n;
	List head = NULL, p = NULL, q = NULL;
	scanf("%d",&n);
	for (int i = 0; i < n; i++) {
		p = (List)malloc(sizeof(list));
		scanf("%d",&p->data);
		p->next = NULL;
		if (head == NULL) {
			head = p;
			q = p;
		} else {
			q -> next = p;
			q = q -> next;
		}
	}

//	for (List L = head; L != NULL; L = L -> next)
//	{
//		printf("%d",L -> data);
//		if (L -> next != NULL) printf(" ");
//	}
//	printf("\n\n\n");
	int m;
	scanf("%d",&m);
	int t,k,d;

for (List L = head; L != NULL; L = L -> next)
		printf("%d ",L -> data);
    printf("\n");

return 0;
} 
```

# 7-3 求解迷宫从入口到出口的路径 (15 分)

![dddd.png](https://blog.fivk.cn/usr/uploads/2021/12/3871161185.png)

### 输入格式:

输入迷宫大小的整数n, 以及n行和n列的二维数组（数组元素1代表障碍物，0代表空位）。

### 输出格式:

依次输出从入口到出口可行路径每个位置的行列下标（i,j），每个位置间用“,”分隔。若没有通路，输出：NO。

### 输入样例1:

```in
4
1 1 1 1
1 0 1 1
1 0 0 1
1 1 1 1
```

### 输出样例1:

```out
(1,1)(2,1)(2,2)
```

### 输入样例2:

### 输出样例2:

```out
(1,1)(1,2)(2,2)(3,2)(3,1)(4,1)(5,1)(5,2)(5,3)(6,3)(6,4)(6,5)(7,5)(8,5)(8,6)(8,7)(8,8)
```

```cpp
#include <bits/stdc++.h>
using namespace std;
#define N 10

bool flag = false;
int n;
int a[N][N];

const int di[] = {0,1,0,-1};
const int dj[] = {1,0,-1,0};

struct Node {
	int i;
	int j;
};

vector<Node> p;
Node t;
void Print()
{
	for (Node node:p)
		printf("(%d,%d)",node.i, node.j);
}

void dfs(int x, int y)
{

if (flag) return;
	if (x == n - 2 && y == n - 2)
	{
		flag = true;
		Print();
		return;
	}

}

int main()
{
	cin >> n;

for (int i = 0; i < n; i ++)
		for (int j = 0; j < n; j++)
			scanf("%d",&a[i][j]);
	t.i = 1;
	t.j = 1;
	p.push_back(t);
	dfs(1,1);
	if (!flag) printf("NO");
}
```

# 7-4 求解迷宫从入口到出口的一条最短路径 (15 分)

![dddd.png](https://blog.fivk.cn/usr/uploads/2021/12/2795296137.png)

### 输入格式:

输入迷宫大小的整数n, 以及n行和n列的二维数组（数组元素1代表障碍物，0代表空位）。

### 输出格式:

### 输入样例1:

```in
4
1 1 1 1
1 0 1 1
1 0 0 1
1 1 1 1
```

### 输出样例1:

```out
(1,1)(2,1)(2,2)
```

### 输入样例2:

### 输出样例2:

```out
(1,1)(2,1)(3,1)(4,1)(5,1)(5,2)(5,3)(6,3)(6,4)(6,5)(7,5)(8,5)(8,6)(8,7)(8,8)
```

```c
#include <stdio.h>

const int di[] = {0,1,0,-1};
const int dj[] = {1,0,-1,0};

int n, head, tail, x, y, a[101], b[101], pre[101], map[12][12];

int f;

void print(int d)
{
	if (pre[d] != 0) print(pre[d]);
		printf("(%d,%d)",a[d],b[d]); 
}

int main()
{
	int i, j;
	scanf("%d",&n);
	for (i = 0; i < n; i++)
		for (j = 0; j < n; j++)
			scanf("%d",&map[i][j]);

head = 0;
	tail = 1;

f = 0;
	map[1][1] = 1;
	a[tail] = 1;
	b[tail] = 1;
	pre[tail] = 0;

while (head != tail)
	{
		head++;
		for (i = 0; i < 4; i++)
		{
			x = a[head] + di[i];
			y = b[head] + dj[i];

# 7-5 公路村村通 (30 分)

现有村落间道路的统计数据表中，列出了有可能建设成标准公路的若干条道路的成本，求使每个村落都有公路连通所需要的最低成本。

### 输入格式:

### 输出格式:

输出村村通需要的最低成本。如果输入数据不足以保证畅通，则输出**−****1**，表示需要建设更多公路。

### 输入样例:

```in
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
```

### 输出样例:

```out
12
```

```cpp
#include <stdio.h>
#include <string.h>
#define N 1001

const int M = 1000;

int u,v,Min[N], mst,G[N][N];
int b[N];

Min[1] = 0;
	mst = 0;

for (int i = 1; i <= n; i++)
	{
		int u = 0, min = M;

for (int j = 1; j <= n; j++)
			if (!b[j] && Min[j] < min)
			{
				min = Min[j];
				u = j;
			}

if (u == 0)
		{
			printf("-1");
			return 0;
		}

b[u] = 1;
		mst += Min[u]; 
		for (int j = 1; j <= n; j++)
			if (!b[j] && Min[j] > G[u][j])
				Min[j] = G[u][j];
	}
	printf("%d",mst);
	return 0;
}
```

# 7-6 最短路径之Dijkstra (10 分)

### 输入样例:

```in
10 34
0 1 2
0 3 5
1 2 5
1 3 2
2 4 8
2 5 4
3 5 4
3 6 2
4 7 5
4 5 2
5 6 3
5 7 9
5 8 7
6 8 7
7 8 3
7 9 4
8 9 8
0
8
```

### 输出样例:

在一行中输出从源点到指定终点的短路径及代价，注意：所有符号均为西文符号。

```out
0-->1-->3-->6-->8:13
```

```c
// #include <stdio.h>
// #include <string.h>

// void print(int pre[], int k, int t)
// {
// 	if (k == -1) return;
// 	print(pre,pre[k],t);
// 	printf("%d",k);
// 	if (k != t) printf("-->");
// }

// 	for (int i = 0; i < e; i++)
// 	{
// 		int x, y, z;
// 		scanf("%d %d %d",&x, &y ,&z);
// 		w[x][y] = w[y][x] = z;
// 	}

// 	int s,t;
// 	scanf("%d %d",&s, &t);

// 	b[s] = 1;

// 不会了，搜的
#include<iostream>
#include<vector>
using namespace std;

#define INF 10001

struct Node{
	int v,l;//一条路的尾结点，该路的长度 
};

```

# 7-7 地下迷宫探索 (30 分)

地道战是在抗日战争时期，在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事，如下图所示。

![](https://images.ptausercontent.com/52)

![](https://images.ptausercontent.com/53)

### 输入格式:

### 输出格式:

### 输入样例1:

```in
6 8 1
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5
```

### 输出样例1:

```out
1 2 3 4 5 6 5 4 3 2 1
```

### 输入样例2:

```
6 6 6
1 2
1 3
2 3
5 4
6 5
6 4
```

### 输出样例2:

```
6 4 5 4 6 0
```

```c
// #include <stdio.h>
// #include <string.h>
// int a[1001][1001];
// int b[1001];
// int count;
// int c[1001], t;
// int n,m,s;
// int TEST = 0;

// int main()
// {
//     while(~scanf("%d %d %d",&n, &m, &s))
//     {
//         fivk();
//     }
// 	return 0;
// }

// 只对了两个测试点

```

# 7-8 最短路径 (20 分)

### 输入格式:

### 输出格式:

如果i和j之间存在路径，则输出"The length of the shortest path between i and j is X."，X为最短路径长度， 否则输出"There is no path between i and j."。

### 输入样例1:

```in
7 6
0 1
2 3
1 4
0 2
1 3
5 6
0 3
```

### 输出样例1:

```out
The length of the shortest path between 0 and 3 is 2.
```

### 输入样例2:

```in
7 6
0 1
2 3
1 4
0 2
1 3
5 6
0 6
```

### 输出样例2:

```out
There is no path between 0 and 6.
```

```c
// #include <stdio.h>
// #include <string.h>
// int w[12][12];
// int dis[12];
// int n,e;
// int b[12];
// int test = 0;

// 	for (int i = 0; i < n; i++)
// 		w[i][i] = 0;

// 	for (int i = 0; i < n; i++)
// 		dis[i] = w[s][i];

// 		if (k == -1)
// 		{
// 			test = 1;
// 			break;
// 		}

// 		b[k] = 1;

// 		for (int j = 0; j < n; j++)
// 		{
// 			if (dis[j] > dis[k] + w[k][j])
// 			{
// 				dis[j] = dis[k] + w[k][j];
// 			}
// 		}
// 	}

// 迪杰斯特拉错了一个点，试试floyde

// floyde也错了一个点，但是分数高一点

```

# 7-9 二叉树的创建与遍历 (5 分)

![PA567.jpg](https://blog.fivk.cn/usr/uploads/2021/12/3328504184.jpg)

### 输入格式:

### 输出格式:

输出为3行整数，每个整数后一个空格。第1行为该二叉树的先根序列，第2行为中根序列，第3行为后根序列。

### 输入样例:

```in
1 5 8 0 0 0 6 0 0
```

### 输出样例:

```out
1 5 8 6 
8 5 1 6 
8 5 6 1 
```

```c
#include <stdio.h>
#include <stdlib.h>

typedef struct tree {
	int x;
	struct tree *lchild;
	struct tree *rchild;
}* Tree;

void print_pre(Tree root)
{
	if (root == NULL)
		return;

printf("%d ",root -> x);
	print_pre(root->lchild);
	print_pre(root->rchild);
}

void print_mid(Tree root)
{
	if (root == NULL)
		return;

print_mid(root->lchild);
	printf("%d ",root -> x);
	print_mid(root->rchild);
}

void print_tail(Tree root)
{
	if (root == NULL)
		return;

print_tail(root->lchild);
	print_tail(root->rchild);
	printf("%d ",root -> x);
}

int main()
{
	Tree root = NULL;
	root = insert(root);
	print_pre(root);
    printf("\n");
	print_mid(root);
    printf("\n");
	print_tail(root);
    printf("\n");
	return 0;
 } 
```

# 7-10 构造哈夫曼树 (20 分)

输入一些单词及其出现的频度，构造一棵哈夫曼树，输出哈夫曼编码的平均码长。

### 输入格式:

输入N，表示有N个单词，以下N行，每一行表示一个单词及其频度。

### 输出格式:

平均码长用浮点数类型表示，保留小数点后5位。

### 输入样例:

在这里给出一组输入。例如：

```in
11
The 1192
of 677
a 541
to 518
and 462
that 242
he 195
is 190
for 157
His 138
are 124
```

### 输出样例:

在这里给出相应的输出。例如：

```out
3.10437
```

# 7-11 快速排序 (10 分)

### 输入格式:

输入为两行，第一行为一个整数n（1<n≤1000），表示数组长度。第二行为n个空格间隔的整数，表示待排序的数组。

### 输出格式:

输出为若干行，每行依次输出Partition后的数组，每个元素后一个空格。

### 输入样例:

```in
5
4 5 3 2 1
```

### 输出样例:

```out
2 1 3 4 5 
1 2 3 4 5 
1 2 3 4 5 
```

int main()
{
	int a[1002];
	scanf("%d",&n);
	for (int i = 0; i < n; i++)
		scanf("%d",&a[i]);
	sort(a,0,n-1);
	for (int i = 0; i < n; i++)
		printf("%d ", a[i]);
    printf("\n");
	return 0;
} 
```

# 7-12 堆排序 (10 分)

对n个数，要求用堆排序（最大堆）对其进行排序。

### 输入格式:

第一行一个n（n<1000）。第二行给出n个数。

### 输出格式:

### 输入样例:

```in
6
7 1 6 4 3 5
```

### 输出样例:

```out
7 4 6 1 3 5 
6 4 5 1 3 7 
5 4 3 1 6 7 
4 1 3 5 6 7 
3 1 4 5 6 7 
1 3 4 5 6 7 
```

```cpp
// 不会，，
//
//  main.cpp
//  Cpp_Homework
//
//  Created by 傅鳕鱼 on 2021/6/16.
//

#include <iostream>
#include <algorithm>
using namespace std;

}

void BuildHeap(int *a,int size)    //建立堆
{
    int i;
    for(i=size/2;i>=1;i--)    //非叶节点最大序号值为size/2
    {
        HeapAdjust(a,i,size);

}
    for(int c=1;c<=size;c++)
        cout<<a[c]<<" ";
    cout<<endl;
}

}
}

# 7-13 二分查找 (20 分)

### 输入格式:

输入共三行： 第一行是n值； 第二行是n个整数； 第三行是x值。

### 输出格式:

输出x所在的下标（0~n-1）及比较次数。若x不存在，输出-1和比较次数。

### 输入样例:

```in
4
1 2 3 4
```

### 输出样例:

```out
0
2
```

# 7-14 统计成绩2 (10 分)

### 输入格式:

输入在第一行中给出一个正整数N（≤6000000），即学生人数；第二行中给出N个学生的百分制成绩（非负整数），其间以空格分隔。

### 输出格式:

在一行中输出A、B、C、D、E对应的五分制成绩的人数分布，数字间以空格分隔，行末不得有多余空格。

### 输入样例:

在这里给出一组输入。例如：

```in
7
77 54 92 73 60 65 69
```

### 输出样例:

在这里给出相应的输出。例如：

```out
1 0 2 3 1
```

# 7-15 建立二叉搜索树并查找父结点 (48 分)

按输入顺序建立二叉搜索树，并搜索某一结点，输出其父结点。

### 输入格式:

输入有三行： 第一行是n值，表示有n个结点； 第二行有n个整数，分别代表n个结点的数据值； 第三行是x，表示要搜索值为x的结点的父结点。

### 输出格式:

输出值为x的结点的父结点的值。 若值为x的结点不存在，则输出：It does not exist. 若值为x的结点是根结点，则输出：It doesn't have parent.

### 输入样例:

```in
2
20
30
20
```

### 输出样例:

```out
It doesn't have parent.
```

###输入样例：

```in
2
20
30
30
```

### 输出样例:

```out
20
```

【数据结构】实验题

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

这是好东西

【Fivk】文章归档

【C++】STL容器的使用时机

【C++】STL常用容器_deque容器

【项目实战】瑞吉外卖-Day03

【开发技巧】Vue2中如何优雅地实现dialog的封装

【Java】继承

【数据结构】实验题