【期末复习】数据科学导论之最后的晚餐

博主： Fivk
发布时间：2021 年 12 月 20 日
1152 次浏览
10356字数
分类： python

# 填空

1.简述数据清洗阶段平滑噪声数据常见的三种方法？

- **分箱**：通过考察数据周围的值，采用近邻来光滑有序数据的值。
- **回归**：查找拟合合两个属性的“最佳”线,使得其中一个属性可以用于预测出另一个属性。
- **聚类**：将离散点组成簇和群。

<p></p></div></div></div>
2.什么是数据变换？

数据变换是将数据转化成适合挖掘的形式。

<p></p></div></div></div>
3.简述什么是最佳拟合线。

最佳拟合线指的是在散点图上绘制的一条直线，使得在这条直线上尽可能多的通过数据点，使大部分数据落在这条线上或离这条线很近。

<p></p></div></div></div>
4.试述购物篮分析法有几种及它们所应用的场所。

购物篮分析法有2种分类。

* 第一类是**美式购物篮分析法** ，适用于**卖场面积大** 、**商品种类多** 、**商品陈列区域距离相差大** 的卖场，类似于沃尔玛；
* 第二类是**日式购物篮分析法** ，适用于**营业面积小** ，**商品种类少** 、**商品陈列区域距离相差小** 的卖场，类似于便利店。

<p></p></div></div></div>
5.请简述什么是大数据傲慢。

大数据傲慢指以为利用大数据分析就可以完全忽略和取代传统数据的收集分析方法。

<p></p></div></div></div>
6.简述基于内容的推荐算法思路和基于人口统计学的推荐算法思路。

基于内容推荐：根据物品的内容来分类，类似的物品间进行推荐。

基于人口统计：给用户来进行分类，根据用户的喜好推荐给相似的用户。

<p></p></div></div></div>
7.简述决策树建立的步骤。

决策树建立的步骤

1. **特征选择**：构建根节点，使所有的训练数据放在根节点，选择最优的特征，分割子集，使得各个子集在当前的条件下有一个好的分类。
2. **决策树的生成**：子集能够基本正确分类则可以构建叶节点，并把这些子集分到所对应的叶节点去，子集如果不能正确分类则选择最优的特征继续进行分割，直到所有的训练子集被基本正确分类。
3. **决策树的修剪**

<p></p></div></div></div>
8.简述什么是数据可视化。

数据可视化是指利用计算机图形学等技术，将数据通过图形化的方式展示出来，直观的表达数据中蕴含的信息，规律和逻辑，便于用户进行观察和理解。

<p></p></div></div></div>
9.可视化的目的是什么？

* 挖掘数据有用信息
* 分析数据形成规律
* 预测数据未来走势

<p></p></div></div></div>
10.可视化的一般过程，包括哪些步骤。

（1）**过滤**：是选择原始数据集的一部分可视化
（2）**映射**：是指将抽象的数据转化为可视化表示的过程
（3）**渲染**：是指通过图形渲染库和显示卡的帮助，把经过映射的数据，以二维或者三维图形的形式绘制出来。
（4）**交互**：是指计算机对用户的某种特定动作，作出反应。

<p></p></div></div></div>
11.简述可视化的原则

1.可视化的首要原则是准确和清洗
2.可视化的结果要阐述事物的相关关系和变化趋势
3.使用用户熟悉的事物进行数据比较
4.构造实物场景，生动的展示数据

# 主观题

### 1.计算准确率与召回率

计算信息检索系统评价指标，一个是准确率，一个是召回率如下图的检索结果，请计算此系统的准确率和召回率。

|                                      | 实际上相关的文档 | 实际上不相关的文档 |
| -------------------------------------- | ------------------ | -------------------- |
| 检索系统返回的、判断为相关的文档     | 15               | 3                  |
| 检索系统不返回的、判断为不相关的文档 | 25               | 10                 |

没什么好分析的看图上公式：

![准确率、召回率.png](https://blog.fivk.cn/usr/uploads/2021/11/2178677838.png)

准确率 = $\frac{15+10}{15+3+25+10}\quad$ = $\frac{25}{53}\quad$

召回率 = $\frac{15}{15+25}\quad$ = $\frac{3}{8}\quad$

### 2.计算K-means

1.假设采用K-means聚类算法将下表的用户分成两类，请描述K-means聚类算法过程，距离函数采用余弦相似度。
</div>

| 用户 | C | D | E |
| ------ | --- | --- | --- |
| 1    | 2 | 3 | 4 |
| 2    | 1 | 5 | 3 |
| 3    | 5 | 4 | 1 |
| 4    | 3 | 3 | 2 |
| 5    | 4 | 1 | 2 |

* 先定义总共有多少个类/簇（cluster）
* 将每个簇心（cluster centers）随机定在一个点上
* 将每个数据点关联到最近簇中心所属的簇上
* 对于每一个簇找到其所有关联点的中心点（取每一个点坐标的平均值）
* 将上述点变为新的**簇心**
* 不停重复，直到每个簇所拥有的点**不变**

*余弦相似度计算公式：*

$$
similarity=cos(\varphi)=\frac{A·B}{|A|·|B|}=\frac{\sum_{i=1}^nA_i×B_i}{\sqrt{\sum_{i=1}^nB_{i}^2}×\sqrt{\sum_{i=1}^nA_{i}^2}}

余弦值越大越越相似。
</div>

```out
答：因为我们要将用户分为两类，所以先任意选取两类，分别为用户2和用户3作为簇1和簇2两类的簇。
各个用户的摸：
|A[1]| = sqrt(2^2+3^2+4^2) = 5.385
|A[2]| = sqrt(1^2+5^2+3^2) = 5.916
|A[3]| = sqrt(5^2+4^2+1^2) = 6.480
|A[4]| = sqrt(3^2+3^2+2^2) = 4.690
|A[5]| = sqrt(4^2+1^2+2^2) = 4.852

计算每个点到两个簇的距离:
到簇1的距离：
Dis_1[1] = (1x2+3x5+4x3)/(A[1]*A[2]) = 29/(5.385*5.916) = 0.910
Dis_1[2] = 1
Dis_1[3] = (1x5+5x4+3x1)/(A[3]*A[2]) = 28/(6.48*5.916) = 0.730
Dis_1[4] = (1x3+5x3+3x2)/(A[4]*A[2]) = 24/(4.69*5.916) = 0.817
Dis_1[5] = (1x4+1x5+2x3)/(A[5]*A[2]) = 15/(4.852*5.916) = 0.522

到簇2的距离：
Dis_2[1] = (5x2+4x3+1x4)/(A[1]*A[3]) = 26/(5.385*6.480) = 0.753
Dis_2[2] = (5x1+4x5+1x3)/(A[2]*A[3]) = 28/(5.916*6.480) = 0.730
Dis_2[3] = 1
Dis_2[4] = (5x3+4x3+1x2)/(A[4]*A[3]) = 29/(4.690*6.480) = 0.921
Dis_2[5] = (5x4+4x1+1x2)/(A[5]*A[3]) = 26/(4.852*6.480) = 0.826

根据第一次分类：
得到
	簇1 有 1，2
	簇2 有 3，4，5
对簇1，簇2取平均值再分类得到一样的分类类别（猜的，再写就没时间了，不可能得到不一样的类别），故停止计算。
综上所述：
	使用余弦相似度分为的两类分别为 1，2，4 和 3，5；

```

2.以下是男性或女性的身高与脚码的统计表。将用K-means聚类算法将它们分成两个性别的集合，中心点初定为第1、第5条数据，采用欧式距离作为距离度量。
</div>

| 用户 | 升高 | 鞋码 | 性别 |
| ------ | ------ | ------ | ------ |
| A    | 179  | 42   | 男   |
| B    | 178  | 43   | 男   |
| C    | 165  | 36   | 女   |
| D    | 177  | 42   | 男   |
| E    | 160  | 35   | 女   |

步骤一样的

直接看公式：

* 欧式距离公式：$d=\sqrt{\sum_{j=1}^n(x_j-y_j)^2}\quad$

$$
比如说A(a_1,b_1,c_1),B(a_2,b_2,c_2):

$$
d=\sqrt{(a_1-a_2)^2+(b_1-b_2)^2+(c_1-c_2)^2}\quad

```out
答：由题意中心点初定为第1、第5条数据，采用欧式距离作为距离度量

所以第一个类的坐标为(179,42),第二个类的距离为(160,35)。

各个数据到第1个类的距离：

dis1[1] = 0

dis1[2] = sqrt[(179-178)^2 + (42-43)^] = sqrt(1+1) = 1.414

dis1[3] = sqrt[(179-165)^2 + (42-36)^2] = sqrt(14^2+6^2) = 15.231

dis1[4] = sqrt[(179-177)^2 + (42-42)^2] = sqrt(2^2) = 2

dis1[5] = sqrt[(179-160)^2 + (42-35)^2] = sqrt(19^2 + 7^2) = 20.248

各个点到第2个类的距离：

dis2[1] = sqrt[(179-160)^2 + (42-35)^2] = sqrt(19^2 + 7^2) = 20.248

dis2[2] = sqrt[(178-160)^2 + (43-35)^2] = sqrt(18^2+8^2) = 19.697

dis2[3] = sqrt[(165 - 160)^2 + (36 - 35)^2] = sqrt(5^2 + 1^2) = 5.099

dis2[4] = sqrt[(177-160)^2 + (42-35)^2] = sqrt(17^2+7^2) = 18.384

dis2[5] = 0

所以

属于类1的用户为A、B、D

属于类2的用户为C、E

取用户的平均值，再次划分类得到的两种类与此结果一样，故停止计算。

综上所述：
	根据要求将他们划分为A、B、D、和C、E两个类别。
```

### 3.朴素贝叶斯(NaiveBayes)算法

比如，现在有如下的文档集，前4个文档是训练集，最后1个文档需要确定其类别。文档分为.两类，分别是日本(Japan)和中国(Chinese)。

[album type="photos"]

![](https://blog.fivk.cn/usr/uploads/2021/12/1837909458.png)
[/album] </div>

- 贝叶斯定理
  - 公式

$P(H|X)=\frac{P(X|H)P(H)}{P(X)}$
  - 特点：需要大量的关于不同事件间概率知识，使用需要**很大的计算成本**
- 朴素贝叶斯分类法
  - 假设：每一个属性都是互相独立的 attributes are conditionally independent
  - **公式**：$P(X|C_i)=\prod^{n}_{k=1} P(x_k|Ci)$

### 4.购物篮记录

1、若某购物篮记录为：

消费者1：啤酒、蛋糕、薯条、阿司匹林

消费者2：尿布、婴儿乳液、葡萄汁、婴儿食品、牛奶

消费者3：雪碧、薯条、牛奶

消费者4：啤酒、牛奶、冰激凌、薯条

消费者5：雪碧、咖啡、牛奶、面包、啤酒

消费者6：啤酒、薯条

请计算：

1) *S* (啤酒→薯条)
2) *S* (牛奶→雪碧)
3) *C* (啤酒→薯条)
4) *L* (啤酒→薯条)

废话少说，上公式

**1.支持度**
</div>

- 支持度$S(A→B)$指的是<span style='color:#A52A2A'>**A与B同时出现的概率**</span>

计算公式：

$S(A→B)=\frac{N(A\&B)}{N}\quad$

**2.置信度**
</div>

- 置信度$C(A→B)$指的是<span style='color:#A52A2A'>**A出现的情况下B同时出现的概率**</span>

计算公式：

$C(A→B)=\frac{N(A\&B)}{N(A)}\quad$

**3.提高度**
</div>

- 提高度$L(A→B)$指的是<span style='color:#A52A2A'>**A出现的情况对于B出现的影响度**</span>

计算公式：

$L(A→B)=\frac{C(A→B)}{S(B)}\quad$

```out
答：根据购物篮记录
(1) S(啤酒->薯条) = 3/6 = 1/2
(2) S(牛奶->雪碧) = 2/6 = 1/3
(3) C(啤酒→薯条) = 3/4
(4) 因为S(薯条) = 4/6 = 2/3
所以L(啤酒->薯条) = C(啤酒->薯条)/S(牛奶) = (3/4)/(2/3) = 9/8
```

### 5.线性回归（最小二乘法）

广告投入和汽车销售量的历史数据如下，假设有一周广告数量为6，预测的汽车销售量是多少？（采用最小二乘法的解法）

- TV：x
- Cars：y

| x | y  |
| --- | ---- |
| 1 | 14 |
| 3 | 24 |
| 2 | 18 |
| 1 | 17 |
| 3 | 27 |

带入最小二乘法方程即可：

$$
y=kx+b

$$
k=\frac{\sum_{i=1}^{n}(x_i-\overline{\text{x}}
)(y_i-\overline{\text{y}}
)}{\sum_{i=1}^{n}(x_i-\overline{\text{x}}
)^2}\quad

$$
b=\overline{\text{y}}-b_1\overline{\text{x}}

```out
答：由题意，假设广告量为自变量x，销售量为应变量y。
所以可设线性回归方程 y = kx+b
其中k为斜率，b为截距。
根据记录表的数据可知：
平均广告量x` = (1 + 3 + 2 + 1 + 3)/5 = 2
平均销售量y` = (14 + 24 + 18 + 17 + 27)/5 = 20
所以 
k = [(1-2)*(14-20)+(3-2)*(24-20)+(2-2)*(18-20)+(1-2)*(17-20)+(3-2)*(27-20)]/[(1-2)^2+(3-2)^2+(2-2)^2+(1-2)^2+(3-2)^2]
   = (-1*(-6)+1*4+(-1)*（-3）+1*7)/(1+1+1+1)
   = 20/4
   = 5

由  b = y` - kx` = 20 - 2*5 = 10
得到回归方程为 y = 5x +10
所以当广告量为 6 时 5*6 + 10 = 40
```

### 6.KNN算法

假设下表是判断糖尿病的训练集，请用K近邻(KNN)算法来预测第7个用户是否患病，若k=3，分别采用欧式距离、余弦相似度为距离度量，请写出预测结果。

| 编号 | A | B | Class(类别1为患病) |
| ------ | --- | --- | -------------------- |
| 1    | 5 | 3 | 0                  |
| 2    | 2 | 6 | 1                  |
| 3    | 4 | 7 | 1                  |
| 4    | 3 | 8 | 0                  |
| 5    | 7 | 5 | 1                  |
| 6    | 1 | 6 | 0                  |
| 7    | 3 | 4 | ?                  |

首先给到需要使用到的公式：

* 欧式距离公式：$d=\sqrt{\sum_{j=1}^n(x_j-y_j)^2}\quad$

$$
比如说A(a_1,b_1,c_1),B(a_2,b_2,c_2):

$$
d=\sqrt{(a_1-a_2)^2+(b_1-b_2)^2+(c_1-c_2)^2}\quad

- 曼哈顿距离公式：$d=\sum_{j=1}^n|x_j-y_j|$

$$
比如说A(a_1,b_1,c_1),B(a_2,b_2,c_2):

$$
d=|a_1-a_2|+|b_1-b_2|+|c_1-c_2|

- 余弦相似度计算公式：

$$
similarity=cos(\varphi)=\frac{A·B}{|A|·|B|}=\frac{\sum_{i=1}^nA_i×B_i}{\sqrt{\sum_{i=1}^nB_{i}^2}×\sqrt{\sum_{i=1}^nA_{i}^2}}

余弦值越大越越相似。
</div>

KNN计算步骤：

1. 计算所有数据与预测数据的距离
2. 按照距离从近到远进行排序
3. 选取k组(一般题目会给出k值)中类别较多的一组
4. 将需要预测的一组归类为广告选取的类别

```out
答：由题意
（1）采用欧氏距离：
使用欧氏距离各个用户与用户7的距离为：
dis[1] = sqrt[(5-3)^2 + (3-4)^2] = sqrt(5)
dis[2] = sqrt[(2-3)^2 + (6-4)^2] = sqrt(5)
dis[3] = sqrt[(4-3)^2 + (7-4)^2] = sqrt(10)
dis[4] = sqrt[(3-3)^2 + (8-4)^2] = sqrt(16)
dis[5] = sqrt[(7-3)^2 + (5-4)^2] = sqrt(17)
dis[6] = sqrt[(1-3)^2 + (6-4)^2] = sqrt(8)

因为k = 3，距离用户7最近的3位用户分别是1、2、6
	其中属于Class = 0 的用户有：1、6
	    属于Class = 1的用户有：2
用户7的邻居属于Class为0居多，故可认为7的Class值为0，
即用户7不患病。
（2）采用余弦相似度
各个用户的模为：
A[1] = sqrt(5^2 + 3^2) = sqrt(34)
A[2] = sqrt(2^2 + 6^2) = sqrt(40)
A[3] = sqrt(4^2 + 7^2) = sqrt(65)
A[4] = sqrt(3^2 + 8^2) = sqrt(90)
A[5] = sqrt(7^2 + 5^2) = sqrt(74)
A[6] = sqrt(1^2 + 6^2) = sqrt(37)
A[7] = sqrt(3^2 + 4^2) = sqrt(25)
使用余弦相似度计算各个用户与用户7的距离
c[1] = (5*3+3*4)/(A[1]*A[7]) = 0.926
c[2] = (2*3+6*4)/(A[2]*A[7]) = 0.948
c[3] = (4*3+7*4)/(A[3]*A[7]) = 0.992
c[4] = (3*3+8*4)/(A[4]*A[7]) = 0.864
c[5] = (7*3+5*4)/(A[5]*A[7]) = 0.953
c[6] = (1*3+6*4)/(A[6]*A[7]) = 0.887
因为k = 3,距离用户7最近的3位用户分别是3、5、2
	其中邻居属于 Class 0的用户不存在，这三个用户均属于Class 1，故根据余弦相似度，
可判断用户7属于Class 1。
```

最后修改：2021 年 12 月 30 日

如果觉得我的文章对你有用，请随意赞赏

【期末复习】数据科学导论之最后的晚餐

Fivk • 2021 年 12 月 20 日

# 填空

1.简述数据清洗阶段平滑噪声数据常见的三种方法？

<p></p></div></div></div>
2.什么是数据变换？

数据变换是将数据转化成适合挖掘的形式。

<p></p></div></div></div>
3.简述什么是最佳拟合线。

最佳拟合线指的是在散点图上绘制的一条直线，使得在这条直线上尽可能多的通过数据点，使大部分数据落在这条线上或离这条线很近。

<p></p></div></div></div>
4.试述购物篮分析法有几种及它们所应用的场所。

购物篮分析法有2种分类。

<p></p></div></div></div>
5.请简述什么是大数据傲慢。

大数据傲慢指以为利用大数据分析就可以完全忽略和取代传统数据的收集分析方法。

<p></p></div></div></div>
6.简述基于内容的推荐算法思路和基于人口统计学的推荐算法思路。

基于内容推荐：根据物品的内容来分类，类似的物品间进行推荐。

基于人口统计：给用户来进行分类，根据用户的喜好推荐给相似的用户。

<p></p></div></div></div>
7.简述决策树建立的步骤。

决策树建立的步骤

<p></p></div></div></div>
8.简述什么是数据可视化。

<p></p></div></div></div>
9.可视化的目的是什么？

* 挖掘数据有用信息
* 分析数据形成规律
* 预测数据未来走势

<p></p></div></div></div>
10.可视化的一般过程，包括哪些步骤。

<p></p></div></div></div>
11.简述可视化的原则

# 主观题

### 1.计算准确率与召回率

计算信息检索系统评价指标，一个是准确率，一个是召回率如下图的检索结果，请计算此系统的准确率和召回率。

没什么好分析的看图上公式：

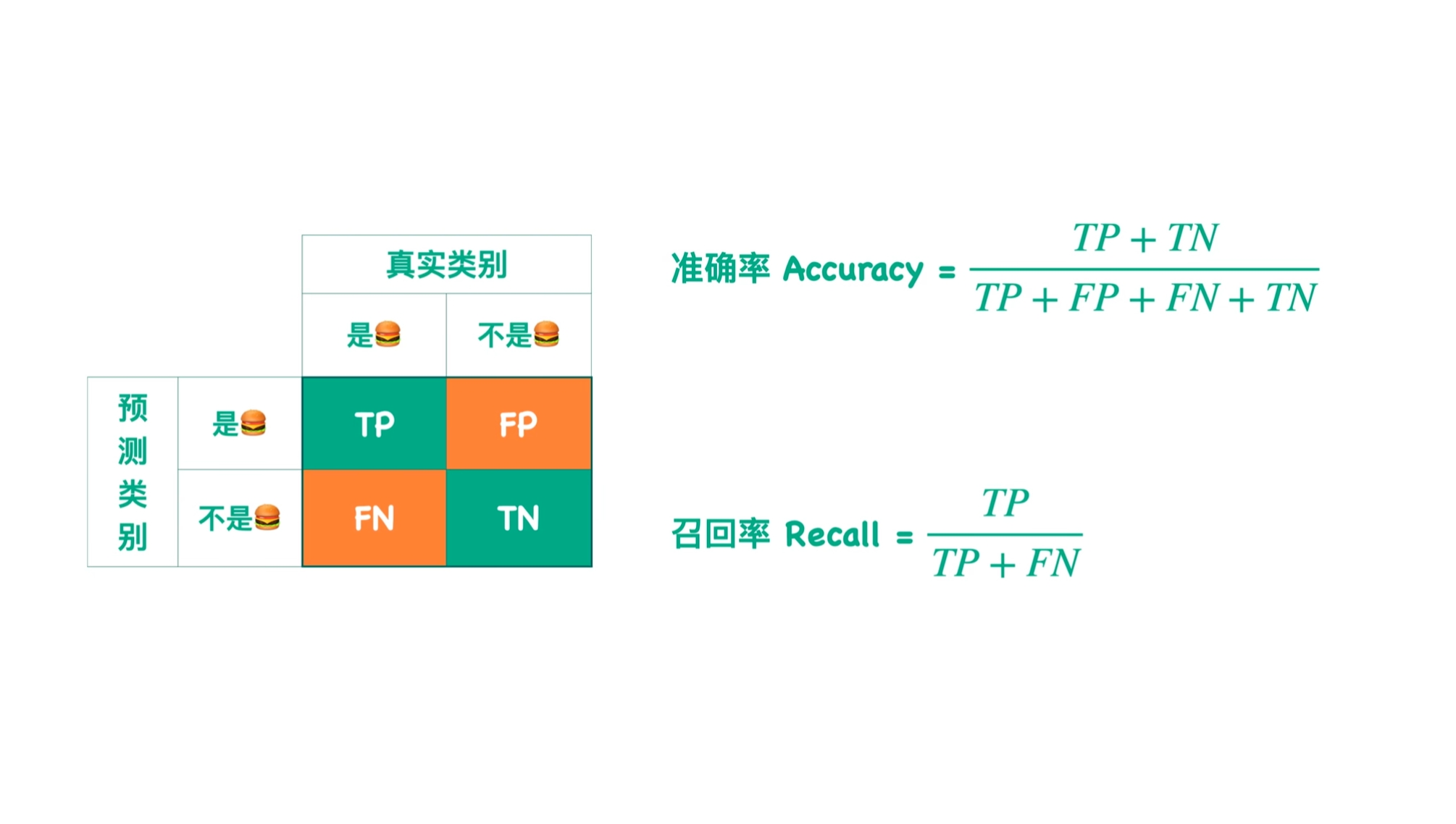![准确率、召回率.png](https://blog.fivk.cn/usr/uploads/2021/11/2178677838.png)

准确率 = $\frac{15+10}{15+3+25+10}\quad$ = $\frac{25}{53}\quad$

召回率 = $\frac{15}{15+25}\quad$ = $\frac{3}{8}\quad$

### 2.计算K-means

1.假设采用K-means聚类算法将下表的用户分成两类，请描述K-means聚类算法过程，距离函数采用余弦相似度。
</div>

| 用户 | C | D | E |
| ------ | --- | --- | --- |
| 1    | 2 | 3 | 4 |
| 2    | 1 | 5 | 3 |
| 3    | 5 | 4 | 1 |
| 4    | 3 | 3 | 2 |
| 5    | 4 | 1 | 2 |

*余弦相似度计算公式：*

$$
similarity=cos(\varphi)=\frac{A·B}{|A|·|B|}=\frac{\sum_{i=1}^nA_i×B_i}{\sqrt{\sum_{i=1}^nB_{i}^2}×\sqrt{\sum_{i=1}^nA_{i}^2}}

余弦值越大越越相似。
</div>

```

步骤一样的

直接看公式：

* 欧式距离公式：$d=\sqrt{\sum_{j=1}^n(x_j-y_j)^2}\quad$

$$
比如说A(a_1,b_1,c_1),B(a_2,b_2,c_2):

$$
d=\sqrt{(a_1-a_2)^2+(b_1-b_2)^2+(c_1-c_2)^2}\quad

```out
答：由题意中心点初定为第1、第5条数据，采用欧式距离作为距离度量

所以第一个类的坐标为(179,42),第二个类的距离为(160,35)。

各个数据到第1个类的距离：

dis1[1] = 0

dis1[2] = sqrt[(179-178)^2 + (42-43)^] = sqrt(1+1) = 1.414

dis1[3] = sqrt[(179-165)^2 + (42-36)^2] = sqrt(14^2+6^2) = 15.231

dis1[4] = sqrt[(179-177)^2 + (42-42)^2] = sqrt(2^2) = 2

dis1[5] = sqrt[(179-160)^2 + (42-35)^2] = sqrt(19^2 + 7^2) = 20.248

各个点到第2个类的距离：

dis2[1] = sqrt[(179-160)^2 + (42-35)^2] = sqrt(19^2 + 7^2) = 20.248

dis2[2] = sqrt[(178-160)^2 + (43-35)^2] = sqrt(18^2+8^2) = 19.697

dis2[3] = sqrt[(165 - 160)^2 + (36 - 35)^2] = sqrt(5^2 + 1^2) = 5.099

dis2[4] = sqrt[(177-160)^2 + (42-35)^2] = sqrt(17^2+7^2) = 18.384

dis2[5] = 0

所以

属于类1的用户为A、B、D

属于类2的用户为C、E

取用户的平均值，再次划分类得到的两种类与此结果一样，故停止计算。

综上所述：
	根据要求将他们划分为A、B、D、和C、E两个类别。
```

### 3.朴素贝叶斯(NaiveBayes)算法

比如，现在有如下的文档集，前4个文档是训练集，最后1个文档需要确定其类别。文档分为.两类，分别是日本(Japan)和中国(Chinese)。

[album type="photos"]

![](https://blog.fivk.cn/usr/uploads/2021/12/1837909458.png)
[/album] </div>

- 贝叶斯定理
  - 公式

### 4.购物篮记录

1、若某购物篮记录为：

消费者1：啤酒、蛋糕、薯条、阿司匹林

消费者2：尿布、婴儿乳液、葡萄汁、婴儿食品、牛奶

消费者3：雪碧、薯条、牛奶

消费者4：啤酒、牛奶、冰激凌、薯条

消费者5：雪碧、咖啡、牛奶、面包、啤酒

消费者6：啤酒、薯条

请计算：

1) *S* (啤酒→薯条)
2) *S* (牛奶→雪碧)
3) *C* (啤酒→薯条)
4) *L* (啤酒→薯条)

废话少说，上公式

**1.支持度**
</div>

- 支持度$S(A→B)$指的是<span style='color:#A52A2A'>**A与B同时出现的概率**</span>

计算公式：

$S(A→B)=\frac{N(A\&B)}{N}\quad$

**2.置信度**
</div>

- 置信度$C(A→B)$指的是<span style='color:#A52A2A'>**A出现的情况下B同时出现的概率**</span>

计算公式：

$C(A→B)=\frac{N(A\&B)}{N(A)}\quad$

**3.提高度**
</div>

- 提高度$L(A→B)$指的是<span style='color:#A52A2A'>**A出现的情况对于B出现的影响度**</span>

计算公式：

$L(A→B)=\frac{C(A→B)}{S(B)}\quad$

### 5.线性回归（最小二乘法）

广告投入和汽车销售量的历史数据如下，假设有一周广告数量为6，预测的汽车销售量是多少？（采用最小二乘法的解法）

- TV：x
- Cars：y

| x | y  |
| --- | ---- |
| 1 | 14 |
| 3 | 24 |
| 2 | 18 |
| 1 | 17 |
| 3 | 27 |

带入最小二乘法方程即可：

$$
y=kx+b

$$
k=\frac{\sum_{i=1}^{n}(x_i-\overline{\text{x}}
)(y_i-\overline{\text{y}}
)}{\sum_{i=1}^{n}(x_i-\overline{\text{x}}
)^2}\quad

$$
b=\overline{\text{y}}-b_1\overline{\text{x}}

由  b = y` - kx` = 20 - 2*5 = 10
得到回归方程为 y = 5x +10
所以当广告量为 6 时 5*6 + 10 = 40
```

### 6.KNN算法

假设下表是判断糖尿病的训练集，请用K近邻(KNN)算法来预测第7个用户是否患病，若k=3，分别采用欧式距离、余弦相似度为距离度量，请写出预测结果。

首先给到需要使用到的公式：

* 欧式距离公式：$d=\sqrt{\sum_{j=1}^n(x_j-y_j)^2}\quad$

$$
比如说A(a_1,b_1,c_1),B(a_2,b_2,c_2):

$$
d=\sqrt{(a_1-a_2)^2+(b_1-b_2)^2+(c_1-c_2)^2}\quad

- 曼哈顿距离公式：$d=\sum_{j=1}^n|x_j-y_j|$

$$
比如说A(a_1,b_1,c_1),B(a_2,b_2,c_2):

$$
d=|a_1-a_2|+|b_1-b_2|+|c_1-c_2|

- 余弦相似度计算公式：

$$
similarity=cos(\varphi)=\frac{A·B}{|A|·|B|}=\frac{\sum_{i=1}^nA_i×B_i}{\sqrt{\sum_{i=1}^nB_{i}^2}×\sqrt{\sum_{i=1}^nA_{i}^2}}

余弦值越大越越相似。
</div>

KNN计算步骤：

【期末复习】数据科学导论之最后的晚餐

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

这是好东西

【Fivk】文章归档

[函数快查] fclose -- 关闭一个打开的文件

【算法基础】二维前缀和

【MySQL】基础

【Java】常用类之包装类

【ACM】大勾股定理(仿2021 520钻石争霸赛7-5—浙江大学陈越)

【期末复习】数据科学导论之最后的晚餐