【Python】线性回归

博主： Fivk
发布时间：2021 年 11 月 08 日
1632 次浏览
暂无评论
3734字数
分类： python

## 简介

</div>

Python之所以如此受欢迎的一个原因就在于它能够应用于数据分析和挖掘方面的工作。不仅是在工业化运用还是在科学研究中，Python提供了非常方便和高性能的应用接口，是人们只需要关注数据本身，而不需要花太多的精力在方法上。

**线性回归** 模型是最常见的统计模型，它反映了系统整体的运动规律。从数学的角度讲，就是根据系统的总体静态观测值，通过算法去除随机性的噪点，发现系统整体运动规律的过程。最简单的线性回归是基于最小二乘法进行拟合的，同时根据自变量的个数，分为**一元线性回归分析** 和**多元线性回归分析** 。

## 一元线性回归分析

</div>

一元线性回归方程如下：

```matlab
y=a*x+b
```

其中a为权重或者斜率，b为截距，我们的目标是研究x和y之间的关系。

假设有如下数据集：

| x     | y     |
| ------- | ------- |
| -3.51 | -4.18 |
| -4.31 | -2.39 |
| -2.68 | -6.33 |
| -3.4  | -4.22 |
| -4.12 | -3.21 |
| -2.81 | -5.62 |
| -3.5  | -4.46 |

我们的目标就是拟合一条线性方程，在这里首先导入需要的库：

```python
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
```

使用`sklearn`库中的 `linear_model` 能够快速搭建训练模型。具体代码如下：

```python
x = [-3.51, -4.31, -2.68, -3.4, -4.12, -2.81, -3.5]
y = [-4.18, -2.39, -6.33, -4.22, -3.21, -5.62, -4.46]
data = pd.DataFrame({'x': x, 'y': y})
x = data[['x']]
y = data['y']
 
# 构建模型
reg = linear_model.LinearRegression()
# 训练模型
reg.fit(x, y)
# 评估模型
print(reg.coef_)        # 斜率
print(reg.intercept_)   # 截距
print(reg.score(x, y))  # R2值
# 预测并可视化
plt.scatter(x, y)
plt.plot(x, reg.predict(x), color='red')
plt.show()
```

在这里输入数据处理稍微复杂，主要是为了构建一个DataFrame型的数据，这样的做法主要是考虑到大多数时候我们都是从文件中读取内容，因而使用pandas读取构建data数据。主要经历以下步骤：

* 接下来调用 `LinearRegression()` 方法构建线性回归模型；
* 训练模型只需要使用 `fit()`函数就能轻松实现；
* 然后分析模型的参数和$R^2$ 值；
* 最终我们将拟合的效果可视化。

输出的结果如下：

```python
[-2.17951421]
-11.91965440487348
0.9715399906543265
```

它的斜率为-2.17，截距为-11.92，$R^2$ 值为0.97。表明x与y之间具有强相关性，并且是负相关的关系。

可视化的图片如下：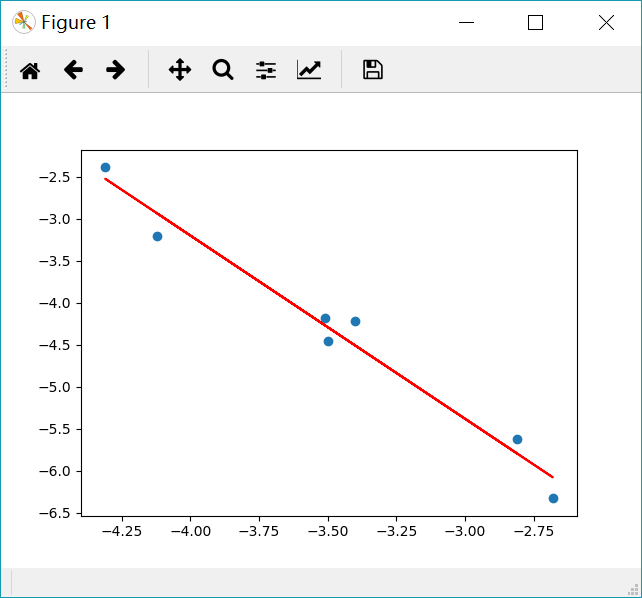

![](https://blog.fivk.cn/usr/uploads/2021/11/510024691.png)

## 多元线性回归分析

</div>

与一元线性回归不同，多元线性回归会出现多个自变量。它的形式如下：

```matlab
y=a*x1+b*x2+c
```

其中a和b为权重，c为截距。

同样，我们考察以下数据集：

| x1    | x2    | y    |
| ------- | ------- | ------ |
| -3.51 | -3.4  | 5.23 |
| -4.31 | -3.93 | 4.25 |
| -2.68 | -2.98 | 6.75 |
| -3.4  | -3.29 | 5.81 |
| -4.12 | -3.88 | 4.7  |
| -2.81 | -2.86 | 6.78 |
| -3.5  | -3.58 | 6.03 |

### 通过Seaborn实现

Seaborn提供了非常方便的可视化接口，能够快速实现线性回归拟合。代码实现如下：

```python
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
 
x1 = [-3.51, -4.31, -2.68, -3.4, -4.12, -2.81, -3.5]
x2 = [-3.4, -3.93, -2.98, -3.29, -3.88, -2.86, -3.58]
y = [5.23, 4.25, 6.75, 5.81, 4.7, 6.78, 6.03]
 
data = pd.DataFrame({'x1': x1, 'x2': x2, 'y': y})
sns.pairplot(data, x_vars=['x1', 'x2'], y_vars='y', kind='reg', size=5)
plt.show()
```

`pairplot()` 函数可以直接将`DataFrame`类型的数据可视化，通过 `kind` 参数选择 `reg` 方法，最终得到如下图：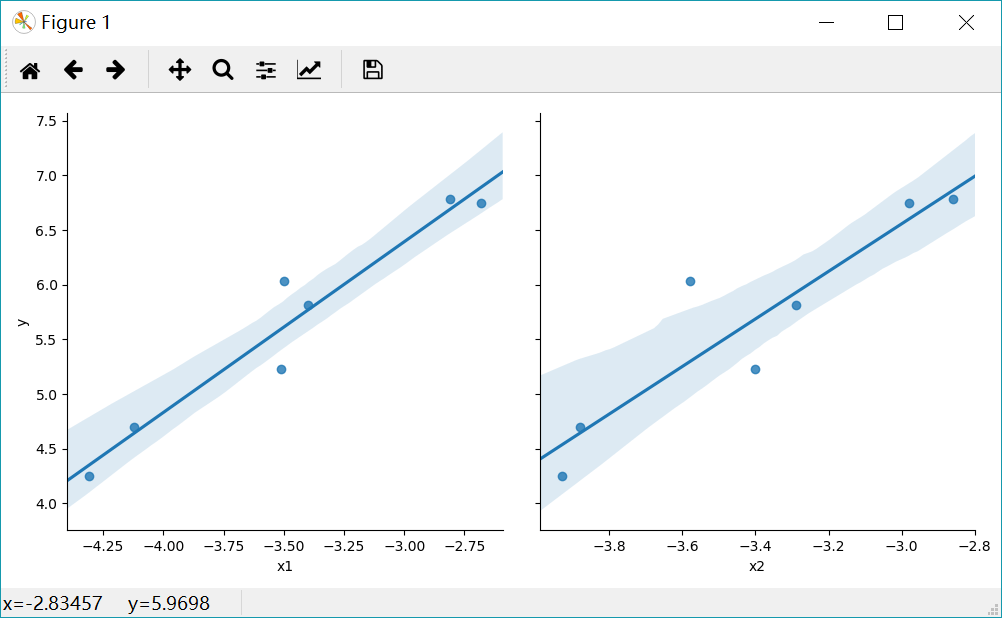

![](https://blog.fivk.cn/usr/uploads/2021/11/4223402728.png)

图中表明（x1，y）和（x2，y）分别具有线性关系，图中带状阴影表示数据的密度，数据越多，该处的阴影越狭窄。

### 通过sklearn实现

同样使用 `LinearRegression` 方法训练数据。代码如下：

```python
import pandas as pd
from sklearn import linear_model
 
x1 = [-3.51, -4.31, -2.68, -3.4, -4.12, -2.81, -3.5]
x2 = [-3.4, -3.93, -2.98, -3.29, -3.88, -2.86, -3.58]
y = [5.23, 4.25, 6.75, 5.81, 4.7, 6.78, 6.03]
data = pd.DataFrame({'x1': x1, 'x2': x2, 'y': y})
x = data[['x1', 'x2']]
y = data['y']
# 构建模型
reg = linear_model.LinearRegression()
# 训练模型
reg.fit(x, y)
# 评估模型
print(reg.coef_)
print(reg.intercept_)
print(reg.score(x, y))
```

输入结果如下：

```matlab
[ 2.24640635 -1.03298326]
9.928015273935468
0.948262589588942
```

y与x1之间斜率为2.25，y与x2之间斜率为-1.03，而我们的模型拟合的$R^2$ 值为0.95，有很强的相关性。

## 总结

</div>

本文主要介绍了以最小二乘法拟合的线性回归方法，sklearn提供了非常方便的模型供我们使用。需要注意的是，sklearn要求x是一个特征矩阵，y是一个NumPy向量。因此，在pandas中x可以是pandas的DataFrame，y可以是pandas的Series。

文章地址：[Python数据挖掘——线性回归 - FINTHON](https://finthon.com/linear-regression/)

</div>

最后修改：2021 年 11 月 09 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

本当迷
哈哈时过境迁再看一遍帆的文章质量还是那么高
挺胸的打工人
感谢博主分享
菜菜
一天就学一些我不知道的东西(´இ皿இ｀)
zhanqy
博主赛高！
null ？？［］
还可以把扩展运算符加上呀，这个很有用［…arr］，用于数组合...

【Python】线性回归

Fivk • 2021 年 11 月 08 日

## 简介

</div>

## 一元线性回归分析

</div>

一元线性回归方程如下：

```matlab
y=a*x+b
```

其中a为权重或者斜率，b为截距，我们的目标是研究x和y之间的关系。

假设有如下数据集：

| x     | y     |
| ------- | ------- |
| -3.51 | -4.18 |
| -4.31 | -2.39 |
| -2.68 | -6.33 |
| -3.4  | -4.22 |
| -4.12 | -3.21 |
| -2.81 | -5.62 |
| -3.5  | -4.46 |

我们的目标就是拟合一条线性方程，在这里首先导入需要的库：

```python
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
```

使用`sklearn`库中的 `linear_model` 能够快速搭建训练模型。具体代码如下：

输出的结果如下：

```python
[-2.17951421]
-11.91965440487348
0.9715399906543265
```

它的斜率为-2.17，截距为-11.92，$R^2$ 值为0.97。表明x与y之间具有强相关性，并且是负相关的关系。

可视化的图片如下：

![](https://blog.fivk.cn/usr/uploads/2021/11/510024691.png)

## 多元线性回归分析

</div>

与一元线性回归不同，多元线性回归会出现多个自变量。它的形式如下：

```matlab
y=a*x1+b*x2+c
```

其中a和b为权重，c为截距。

同样，我们考察以下数据集：

### 通过Seaborn实现

Seaborn提供了非常方便的可视化接口，能够快速实现线性回归拟合。代码实现如下：

`pairplot()` 函数可以直接将`DataFrame`类型的数据可视化，通过 `kind` 参数选择 `reg` 方法，最终得到如下图：

![](https://blog.fivk.cn/usr/uploads/2021/11/4223402728.png)

图中表明（x1，y）和（x2，y）分别具有线性关系，图中带状阴影表示数据的密度，数据越多，该处的阴影越狭窄。

### 通过sklearn实现

同样使用 `LinearRegression` 方法训练数据。代码如下：

输入结果如下：

```matlab
[ 2.24640635 -1.03298326]
9.928015273935468
0.948262589588942
```

y与x1之间斜率为2.25，y与x2之间斜率为-1.03，而我们的模型拟合的$R^2$ 值为0.95，有很强的相关性。

## 总结

</div>

文章地址：[Python数据挖掘——线性回归 - FINTHON](https://finthon.com/linear-regression/)

</div>

【Python】线性回归

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

【Fivk】文章归档

回忆刚入天柱二中的我

【算法基础】离散化

【Python】线性回归

【Docker】docker启动MongoDB简单方法

【C】二进制的分析（原码反码补码）

【前端笔记】JavaScript

【Python】线性回归

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【Python】线性回归

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款