【数据结构】图论算法_最小树生成

博主： Fivk
发布时间：2021 年 08 月 22 日
1248 次浏览
3401字数
分类：数据结构

# 一、什么是图的最小生成树（MST）

不知道大家还记不记得树的一个定理：N个点用 N - 1 条边连接成一个连通块，形成的图形只可能是树，没有别的可能。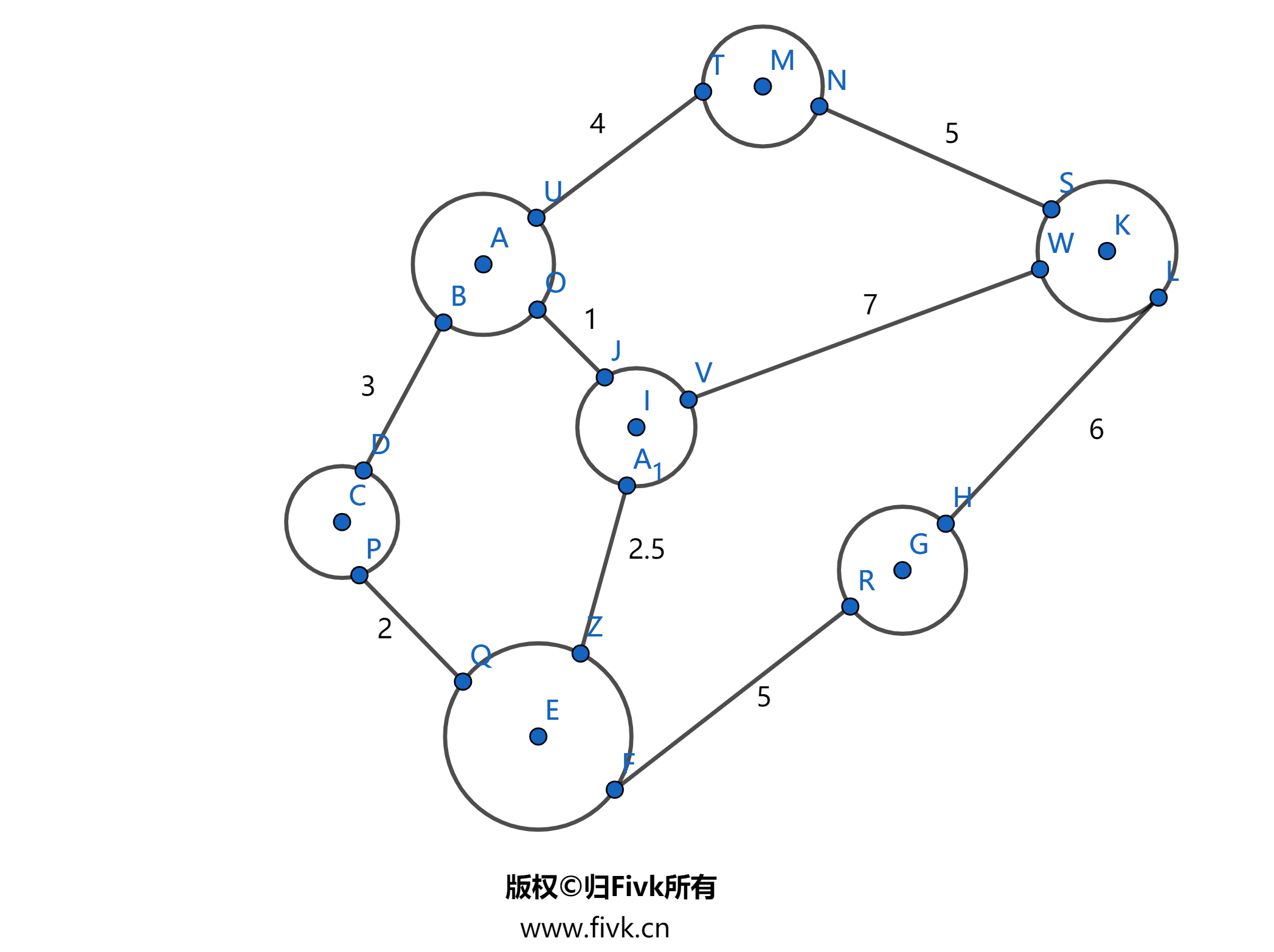

![](https://blog.fivk.cn/usr/uploads/2021/08/1983932691.png)

一个有 N 个顶点的图，边一定是大于等于 N - 1 条的。图的最小生成树，就是在这些边中选择 N - 1 条出来，连接所有的 N 个顶点。这 N - 1 条边的边权之和是所有方案中最小的。

# 二、最小生成树用来解决什么问题？

就是用来解决如何用最小的“代价”用 N - 1条边连接 N 个点的问题。例如：

**例 城市公交网建设问题**

> 【问题描述】
>
> 有一张城市地图，图中的顶点为城市，无向边代表两个城市间的连通关系，边上的权为这两个城市之间修建高速公路的造价，研究后发现，这个地图有一个特点，即任意一对城市都是连通的。现在的问题就是，要修建若干高速公路把所有的城市联系起来，问如何设计可使得工程总造价最少？
>
> 【输入格式】
>
> n（城市数，1<=n<=100）
>
> e（边数）
>
> 以下 e 行，每行3个数 i、j、$w_{ij}$，表示在城市 i、j 之间修建高速公路的造价。
>
> 【输出格式】
>
> n - 1 行，每行为两个城市的序号，表明这个两个城市间建一条高速公路。
>
> 【输入样例】
>
> ```cpp
> 5 8
> 1 2 2
> 2 5 9
> 5 4 7
> 4 1 10
> 1 3 12
> 4 3 6
> 5 3 3
> 2 3 8
> ```
>
> 【输出样例】
>
> ```cpp
> 1 2
> 2 3
> 3 4
> 3 5
> ```

# 三、Prim 算法

Prim 算法采用与 Dijkstra、Bellman—Ford 算法一样的“蓝白点”思想：白点代表已经进入最小生成树的点，蓝点代表未进入最小生成树的点。

**算法描述**：

> 以 1 为起点生成最小树，min[v] 表示蓝点 v 与白点相连的最小边权。
>
> MST 表示最小生成树的权值之和。
>
> - (a) 初始化 ： min[v] = ∞ （v!=1）；min[1] = 0；MST = 0；
> - (b) for(i = 1; i <= n; i++)
>   1. 寻找 min[u] 最小的蓝点 u。
>   2. 将 u 标记为白点。
>   3. MST += min[u]。
>   4. for 与 u 相连的所有蓝点 v
>
>      ```cpp
>      if(min[v] > w[u][v])
>          min[v] = w[u][v];
>      ```
> - (c) 算法结束：MST 即为最小生成树的权值之和。
>
> 算法的时间复杂度：$O(N^2)$。

**例题 最优布线问题(wire)**

> 【问题描述】
>
> 学校有 n 台计算机，为了方便数据传输，现在要将它们用数据线连接起来。两台计算机被连接是指它们有数据线连接。由于计算机所处的位置不同，因此不同的两台计算机的连接费往往是不同的。
>
> 当然，如果将任意两台计算机都用数据线连接，费用将是相当庞大的。为了节省费用，我们采用数据的间接传输手段，即一台计算机可以间接的通过若干台计算机（作为中转）来实现与另一台计算机的连接。
>
> 现在由你负责连接这些，计算机，任务是任意两台计算机都连通（不管是直接还是间接的）。
>
> 【输入格式】
>
> 输入文件 wire.in，第一行为整数 n （2 <= n <= 100），表示计算机的数目。此后 n 行，每行 n 个整数。第 x + 1 行 y 列的整数表示直接连接第 x 台计算机和 y 台计算机的费用。
>
> 【输出格式】
>
> 输出文件 wire.out，一个整数，表示最小的连接费用。
>
> 【输入样例】
>
> ```in
> 3
> 0 1 2
> 1 0 1
> 2 1 0
> ```
>
> 【输出格式】
>
> ```out
> 2
> ```
>
> 【参考程序】
>
> ```cpp
> #include <iostream>
> #include <cstring>
> using namespace std;
>
> bool b[101];    // 记录 蓝白点
> int Min[101];   // 表示蓝点 v 与 白点相连的最小边权
> int f[101][101];
> int n,MST;
>
> int main()
> {
>     cin >> n;
>     for(int i = 1; i <= n; i++)
>         for(int j = 1; j <= n; j++)
>             cin >> f[i][j];
>
>     // (a) 初始化
>     memset(Min,0x7f,sizeof(Min));
>     Min[1] = 0;
>     MST = 0;
>     //b[1] 不用初始化，应为后面算法要用到 ，不确定 1 是不是最短
>
>     // (b) 算法开始
>     for(int i = 1; i <= n; i++)
>     {
>         int u = 0,min = 0x7fffffff;
>
>         // 寻找最小的 Min[v]
>         for(int j = 1; j <= n; j++)
>         if(!b[j] && Min[j] < min)
>         {
>             min = Min[j];
>             u = j;
>         }
>
>         if(u == 0) break;
>
>         // 将 u 标记为白点
>         b[u] = true;
>         MST += Min[u];
>
>         // 更新 与u相连的所有蓝点 v
>         for(int j = 1; j <= n; j++)
>             if(!b[j] && Mij[j] > f[u][j])
>                 Min[j] = f[u][j];
>     }
>     cout << MST << endl;
>     system("pause");
>     return 0;
> }
> ```
>
> ![是不是太简单了？哈哈哈](https://blog.fivk.cn/usr/uploads/2021/08/459482078.png)

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-8b2023930e02941388345577b543933215" aria-expanded="true"><div class="accordion-toggle"><span style="">老师上课的内容</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-8b2023930e02941388345577b543933215" class="collapse collapse-content"><p></p>

100 表示无穷大

输入数据：

```in
6
100 006 001 005 100 100
006 100 005 100 003 100
001 005 100 007 005 004
005 100 007 100 100 002
100 003 005 100 100 006
100 100 004 002 006 100
```

Code:

```c
#include <stdio.h>
#define N 20

typedef struct {
	int s, e;		// 起点 终点 
	int w;			// 权值 
}ED;

void Prim(int a[N][N], int n, ED edge[])
{
	int i, j, k, m, c;				
	ED e;

for (i = 0; i < n; i++) 		/*边表初始化*/
	{                    
		edge[i].s = 0;
		edge[i].e = i + 1;
		edge[i].w = a[0][i+1];
	}

for (j = 0; j <= n - 2; j++) 
	{
		for (m = j, k = j + 1; k <= n - 2; k++) 	/*选定最小边*/ 
			if (edge[k].w < edge[m].w)
				m = k;
			
		e = edge[j];
		edge[j] = edge[m];
		edge[m] = e;								// 交换，表示下一次不会使用，k从j+1个开始，交换后，以后不会选取这条
	
		for (k = j + 1; k <= n -2; k++)				/*修改其余边*/ 
			if (edge[k].w > a[edge[j].e][edge[k].e])
			{
				edge[k].s = edge[j].e;
				edge[k].w = a[edge[j].e][edge[k].e];
			}
	}
}

int main()
{
	ED edge[N];
	int a[N][N],mw;
	int i, j, n, k;

scanf("%d",&n);
	for (i = 0; i < n; i++)
		for (j = 0; j < n; j++)
			scanf("%d",&a[i][j]);
	printf("\n");
	Prim(a,n,edge);

for (mw = 0, k = 0; k < n - 1; k++)
	{
		printf("%d %d %d\n",edge[k].s, edge[k].e,edge[k].w);
		mw += edge[k].w;
	}
	printf("\nW = %d\n",mw);
	return 0;
}
```

最后修改：2021 年 11 月 12 日

如果觉得我的文章对你有用，请随意赞赏

【数据结构】图论算法_最小树生成

Fivk • 2021 年 08 月 22 日

# 一、什么是图的最小生成树（MST）

不知道大家还记不记得树的一个定理：N个点用 N - 1 条边连接成一个连通块，形成的图形只可能是树，没有别的可能。

![](https://blog.fivk.cn/usr/uploads/2021/08/1983932691.png)

# 二、最小生成树用来解决什么问题？

就是用来解决如何用最小的“代价”用 N - 1条边连接 N 个点的问题。例如：

**例 城市公交网建设问题**

# 三、Prim 算法

Prim 算法采用与 Dijkstra、Bellman—Ford 算法一样的“蓝白点”思想：白点代表已经进入最小生成树的点，蓝点代表未进入最小生成树的点。

**算法描述**：

**例题 最优布线问题(wire)**

100 表示无穷大

输入数据：

```in
6
100 006 001 005 100 100
006 100 005 100 003 100
001 005 100 007 005 004
005 100 007 100 100 002
100 003 005 100 100 006
100 100 004 002 006 100
```

Code:

```c
#include <stdio.h>
#define N 20

typedef struct {
	int s, e;		// 起点 终点 
	int w;			// 权值 
}ED;

void Prim(int a[N][N], int n, ED edge[])
{
	int i, j, k, m, c;				
	ED e;

for (i = 0; i < n; i++) 		/*边表初始化*/
	{                    
		edge[i].s = 0;
		edge[i].e = i + 1;
		edge[i].w = a[0][i+1];
	}

int main()
{
	ED edge[N];
	int a[N][N],mw;
	int i, j, n, k;

scanf("%d",&n);
	for (i = 0; i < n; i++)
		for (j = 0; j < n; j++)
			scanf("%d",&a[i][j]);
	printf("\n");
	Prim(a,n,edge);

for (mw = 0, k = 0; k < n - 1; k++)
	{
		printf("%d %d %d\n",edge[k].s, edge[k].e,edge[k].w);
		mw += edge[k].w;
	}
	printf("\nW = %d\n",mw);
	return 0;
}
```

【数据结构】图论算法_最小树生成

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

这是好东西

【Fivk】文章归档

【C++】STL常用算法_谓词

【c】质数判断

【Java】常用类之File

【Spring】概念知识回顾

【前端笔记】JavaScript

【数据结构】图论算法_最小树生成