【数据结构】二叉树

博主： Fivk
发布时间：2021 年 07 月 13 日
1194 次浏览
暂无评论
4051字数
分类：数据结构

# 一、二叉树基本概念

二叉树(binary tree,简写成BT)是一种特殊的树型结构,它的度数为2的树。即二叉树的每个结点最多有两个子结点。每个结点的子结点分别称为左孩子、右孩子,它的两棵子树分别称为左子树、右子树。二叉树有5中基本形态: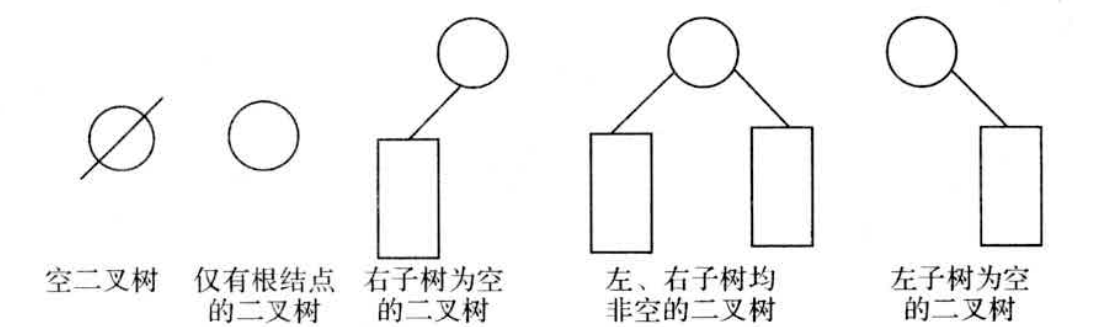

![](https://blog.fivk.cn/usr/uploads/2021/07/1734372890.png)

前面引入的树的术语也基本适用于二叉树,但二叉树与树也有很多不同,如:首先二叉树的每个结点至多只能有两个子结点,二叉树可以为空,二叉树一定是有序的,通过它的左、右子树关系体现出来。

# 二、二叉树的性质

* 【性质1】在二叉树的第i层上最多有$2^{n-1}$个结点(i>=1)。
  证明:很简单,用归纳法:当i=1时,$2^{i-1}=1$显然成立;现在假设第i-1层时命题成立，即第i—1层上最多有$2^{i-1}$个结点。由于二叉树的每个结点的度最多为⒉,故在第i层上的最大结点数为第i一1层的2倍,即$2*2^{i-2}=2^{i-1}$。
* 【性质2】深度为k的二叉树至多有$2^k-1$个结点(k≥1)。
  证明:在具有相同深度的二叉树中,仅当每一层都含有最大结点数时,其树中结点数最多。因此利用性质1可得,深度为k的二叉树的结点数至多为:

$2^0+2^1+2^2+2^3+...+2^{k-1}=2^k-1$

故命题正确。
  特别:一棵深度为k且有$2^k-1$个结点的二叉树称为满二叉树。如图A为深度为4的满二叉树,这种树的特点是每层上的结点数都是最大结点数。

可以对满二叉树的结点进行连续编号,约定编号从根结点起,自上而下,从左到右,由此引出完全二叉树的定义,深度为k,有n个结点的二叉树当且仅当其每一个结点都与深度为k 的满二叉树中编号从1到n的结点—一对应时,称为完全二叉树。

图B就是一个深度为4,结点数为12的完全二叉树。它有如下特征:叶结点只可能在层次最大的两层上出现;对任一结点,若其右分支下的子孙的最大层次为m,则在其左分支下的子孙的最大层次必为m或m+1。图C,D不是完全二叉树,请大家思考为什么?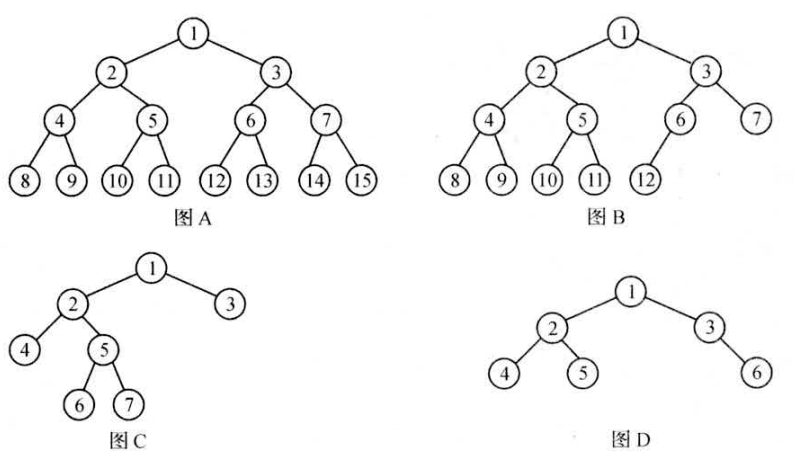

![](https://blog.fivk.cn/usr/uploads/2021/07/3513745431.png)

【性质3】对任意一棵二叉树,如果其叶结点数为$n_0$度为2的结点数为$n_2$,则一定满足:$n_0=n_2+1$。
证明:因为二叉树中所有结点的度数均不大于2,所以结点总数(记为n)应等于0度结点数$n_0$、1度结点n和2度结点数$n_2$:之和:

$n=n_0+n_1+n_2$        (式子1)
另一方面,1度结点有一个孩子,2度结点有两个孩子,故二叉树中孩子结点总数是:$n_1+2n_2$
树中只有根结点不是任何结点的孩子,故二叉树中的结点总数又可表示为:

$n-1=n_1+n_2$        (式子2)
由式子1和式子2得到:$n_0=n_2+1$

【性质4】具有n个结点的完全二叉树的深度为$floog(log2_n)+1$
证明:假设深度为k,根据完全二叉树的定义,前面k一1层一定是满的,所以$n>2^{k-1}-1$。但n又要满足$n<=2^k-1$,所以,$2^{k-1}-1<n<=2^k-1$，变换一下为$2{k-1}<=n<2^k$。以2为底取对数得到：$k-1<=log_2n<k$。而k是整数，所以$k=floor(log_2n)+1$。

【性质5】对于一棵n个结点的完全二叉树,对任一个结点(编号为i),有:

1. 如果i=1,则结点i为根,无父结点;如果i>1,则其父结点编号为i/2。
   如果$2*i>n$,则结点i无左孩子(当然也无右孩子,为什么?即结点i为叶结点);否则左孩子编号为2*i。
2. 如果$2*i+1>n$,则结点i无右孩子;否则右孩子编号为$2*i+1$。证明:略,我们只要验证一下即可。总结如图: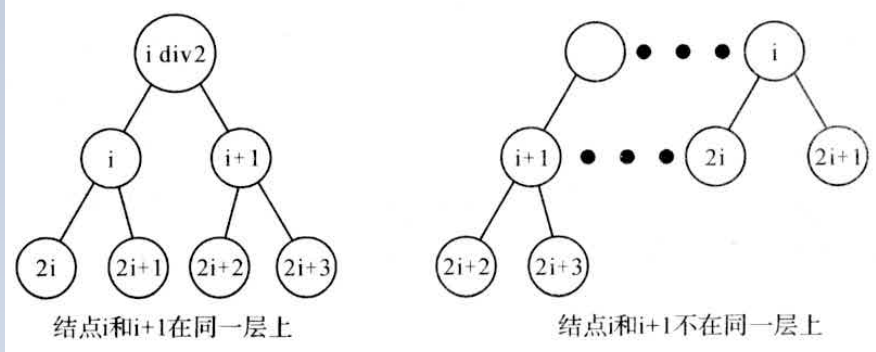

![](https://blog.fivk.cn/usr/uploads/2021/07/2824171434.png)

# 三、二叉树的存储结构

> （1）**链式存储结构**：即单链表结构或双链表结构（同树）。数据结构修改如下：

```cpp
typedef struct node;
typedef node* tree;
struct node
{
	char data;
	tree lchild,rchild;
};
tree bt;
```

或

```cpp
typedef struct node;
typedef node* tree;
struct node
{
	char data;
	tree lchild,rchild,father;
};
tree bt;
```

如图A的一颗二叉树用单链表就可以表示成如图B的形式：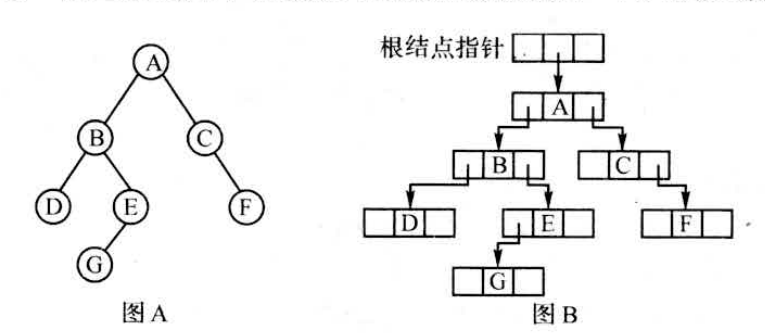

![](https://blog.fivk.cn/usr/uploads/2021/07/1478096122.png)

> （2）**顺序储存结构**：即几个数组加一个指针变量。数据结构如下：

```cpp
const int n=10;
char data[n];
char lchild[n];
char rchild[n];
int bt;			//根结点指针
```

二叉树在处理表达式时经常用到，一般用叶结点表示运算元，分界点表示运算符。这样的二叉树称为表达式树。如现在有一个表达式：$(a+b/c)*(d-e)$，可以用图表示：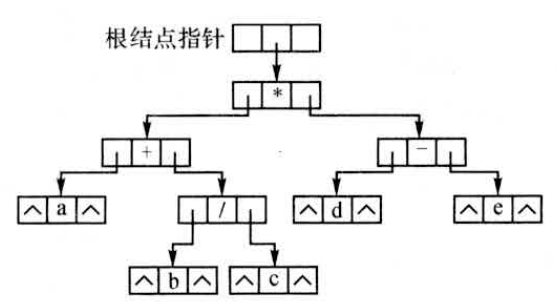

![](https://blog.fivk.cn/usr/uploads/2021/07/1985862166.png)

数据结构定义如下：

按表达式的书写顺序逐个编号，分别为1...9，注意表达式中的所有括号在树中是不出现的，因为表达式树本身就是有序的。叶结点的左右子树均为空（用0表示）。

```cpp
char data[9]={'a','+','b','/','c','*','d','-','e'};
int lchild[9]={0,1,0,3,0,2,0,7,0};
int rchild[9]={0,4,0,5,0,8,0,9,0};
int bt;			//结点点指针，初值=6,指向'*'
```

二叉树的操作：最重要的是遍历二叉树，但基础又是建一颗二叉树、插入一个结点到二叉树中、删除结点或子树等。
</div>

**例 3.3 医院设置**

【问题描述】

设有一颗二叉树如图，其中圈中的数字表示结点中居民的人口，圈边上的数字表示结点编号。现在要求在某个结点上建立一个医院，即所有居民所走的路径之和为最小，同时约定，相邻结点之间距离为1，就本图而言，若医院建在1处，则距离和$=4+12+2*20+2*40=136$；若医院建在3处，则距离和$=4*2+13+20+40=81$...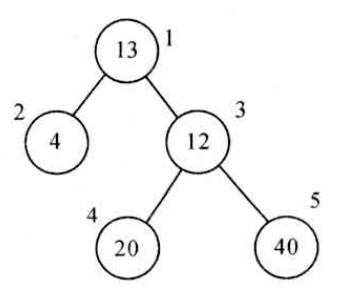

![](https://blog.fivk.cn/usr/uploads/2021/07/54869262.png)

</div>

【输入格式】

输入文件名为hospital.in，其中第一行一个整数n，表示树的结点树（n<=100）。接下来的n行每行描述了一个结点的状况，包含三个整数，整数之间用空格(一个或多个)分割，其中：第一个数为居民人口数；第二个数为左链接，为0表示无链接；第三个数为右链接，为0表示无链接。

【输出格式】

输出文件为hospital.out，该文件只有一个整数，表示最小距离和。

【输入格式】

```in
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
```

【输出样例】

```out
8
```

这是一道简单的二叉树应用问题，问题中的结点数并不多，数据规模也不大，采用邻接矩阵储存，用Floyed求出任意两个结点之间的最短路径，然后穷举医院可能建立的n个结点位置，找出一个最小距离的位置即可。当然也可以用双链表结构或带父结点信息的数组存储结构来解决，但实际操作稍微麻烦了一点。

```cpp
#include<iostream>
#include<cstdlib>
#include<cstdio>
using namespace std;
int a[101];
int g[101][101];
int main()
{
    int n,i,j,k,l,r,min,total;
    freopen("hospital.in","r",stdin);
    freopen("hospital.out","w",stdout);

cin>>n;

for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            g[i][j]=1000000;

for(i=1;i<=n;i++)   //读入、初始化
    {
        g[i][i]=0;
        cin>>a[i]>>l>>r;
        if(l>0) g[i][l]=g[l][i]=1;
        if(r>0) g[i][r]=g[r][i]=1;
    }

for(k=1;k<=n;k++)   //用Floyed求任意两结点之间的最短路径
        for(i=1;i<=n;i++)
        if(i!=k)
            for(j=1;j<=n;j++)
            if(i!=j && k!=j && g[i][k] + g[k][j] < g[i][j])
                g[i][j]=g[i][k]+g[k][j];
  
    min=0x7fffffff;

for(i=1;i<=n;i++)
    {
        total=0;
        for(j=1;j<=n;j++)
            total+=g[i][j]*a[j];
        if(total<min) min=total;
    }

cout<<min<<endl;

fclose(stdin);
    fclose(stdout);

system("pause");
    return 0;
}
```

后记：

在各种竞赛中经常遇到这样的问题：n-1条公路连接着n个城市，从每个城市出发都可以通过公路到达其他任意城市。每个城市里面都有一定数量的居民，但是数量并不一定相等，每条公路的长度也不一定相等。x公司（或者是政府）决定在某一个城市建立一个医院/酒广/游乐场……问：将它建在哪，可以使所有居民移动到那里的总消耗最小？这种题目都是本题的“变形”，一般称为“树的中心问题”。除了简单的穷举法之外，还有更好的时间复杂度为$O(n)$的算法，我们将在后续继续讨论。

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-f990fb31f09f300be9e72a5c5f86a73d38" aria-expanded="true"><div class="accordion-toggle"><span style="">floyed算法例题</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-f990fb31f09f300be9e72a5c5f86a73d38" class="collapse collapse-content"><p></p>

【问题描述】

平面上有n个点(N<=100)，每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点直线的距离。现在的任务是找出从一点到另一点之间的最短路径。

</div>

【输入格式】

第1行为整数n。
第2行到第n+1行（共n行），每行两个整数x和y，描述了一个点的坐标（以一个空格分隔）。
第n+2行为一个整数m，表示图中连线的个数。
此后的m行，每行描述一条连线，由两个整数i和j组成，表示第1个点和第j个点之间有连线。
最后一行：两个整数s和t，分别表示源点和目标点。
【输出格式】

仅1行，一个实数（保留两位小数），表示从s到t的最短路径长度。

```in
5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5
```

```out
3.41
```

```cpp
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;

int a[101][3];
double f[101][101];

int main()
{

int i,j,k,total,min;
    int n,m,x,y,s,t;

memset(f,0x7f,sizeof(f));

cin>>n;

for(i=1;i<=n;i++)
        cin>>a[i][1]>>a[i][2];
    cin>>m;

for(i=1;i<=m;i++)
    {
        cin>>x>>y;
        f[x][y]=f[y][x]=sqrt(pow(double(a[x][1]-a[y][1]),2)+pow(double(a[x][2]-a[y][2]),2));
    }

cin>>s>>t;

for(k=1;k<=n;k++)
        for(i=1;i<=n;i++)
            if(k!=i)
            for(j=1;j<=n;j++)
            if(j!=i && j!=k && f[i][j]>f[k][j]+f[i][k])
            f[i][j]=f[k][j]+f[i][k];

printf("%.2lf\n",f[s][t]);

return 0;
}
```

# 四、遍历二叉树

在二叉树的应用中,常常要求在树中查找具有某种特征的结点,或者对全部结点逐一进行某种处理,这就是二叉树的遍历问题。所谓二叉树的遍历是指按一定的规律和次序访问树中的各个结点,而且每个结点仅被访问一次。“访问”的含义很广,可以是对结点作各种处理，如输出结点的信息等。遍历一般按照从左到右的顺序,共有3种遍历方法,先(根)序遍历，中(根)序遍历,后(根)序遍历。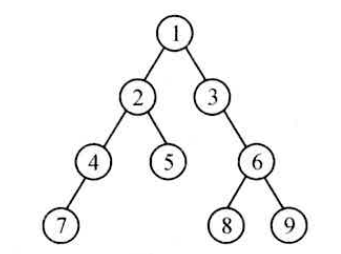

![](https://blog.fivk.cn/usr/uploads/2021/07/3775628437.png)

> （一）先序遍历的操作定义如下

若二叉树为空，则空操作返回，否则：

1. 访问根结点
2. 先序遍历左子树
3. 先序遍历右子树

先序遍历树结果为：124753689

数据结构如下：

```）cpp
void preorder(tree bt)	//先序遍历根结点为bt的二叉树的递归算法
{
	if(bt)
	{
		cout<<bt->data;			//显示结点数据，可以更改为其他对结点的操作
		preorder(bt->lchild);		//先序遍历左子树
		preorder(bt->rchild);		//先序遍历右子树
	}
}
```

> （二）中序遍历的操作定义如下：

若二叉树为空，则空操作返回，否则：

1. 中序遍历左子树
2. 访问根结点
3. 中序遍历右子树

数据结构如下：

```））cpp
void postorder(tree bt)		//后序遍历根结点为bt的二叉树的递归算法
{
	if(bt)
	{
		postorder(bt->lchild);	//中序遍历左子树
		cout<<bt->data;		//显示结点数据，可以更改为其他对结点的操作
		postorder(bt->rchild);	//中序遍历右子树
	}
}
```

> （三）后序遍历的操作定义如下：

若二叉树为空，则空操作返回，否则：

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根节点

后序遍历结果为：745289631

```cpp
void postorder(tree bt)		//后序遍历根节点为bt的二叉树的递归算法
{
	if(bt)
	{
		postorder(bt->rchild);	//后序遍历左子树
		postorder(bt->lchild);	//后序遍历右子树
		cout<<bt->data;		//显示结点数据，可以更改为其他对结点的操作
	}
}
```

> （四）层序遍历的操作定义如下：

若二叉树为空，则空操作返回，否则：

1. 从树的第一层（也就是根结点）访问
2. 从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。

如下图所示，遍历的顺序为：ABCDEFGHL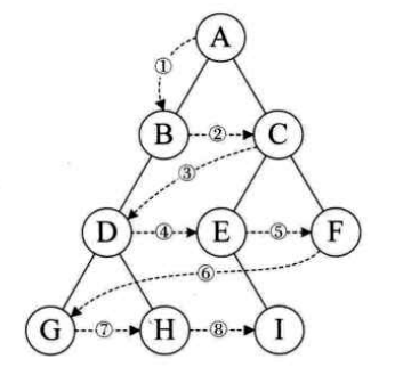

![](https://blog.fivk.cn/usr/uploads/2021/07/3482429990.png)

```cpp
bool Leveltraverse(tree bt)
{
	tree p;
	if(!bt)
		return false;
	queue<tree> Q;	//创建一个普通队列（先进后出），里面存放指针类型
	Q.push(bt);	//根指针入队
	while(!Q.empty())
	{		//如果队列不空
		p=Q.front();	//取出队头元素作为当前扩展结点livenode
		Q.pop();	//弹出队头元素

cout<<p->data<<"  ";
		fi(p->lchild)
			Q.push(p->lchild);
		if(p->rchild)
			Q.push(p->rchild);
	}
	return true;
}
```

当然我们还可以改用栈实现的非递归过程，这里我们就不探究了。

</div>

关于前面讲的表达式树，我们可以分别用先序、中序、后序的遍历方法得出完全不同的遍历结果，如对下图遍历结果如下，它们正好对应着表达式的3中表示方法。

* $-+a*b-cd/rf$（前缀表式，波兰式）
* $a+b*c-d-e/f$（中缀表达）
* $abcd-*+ef/-$（后缀表示，逆波兰式）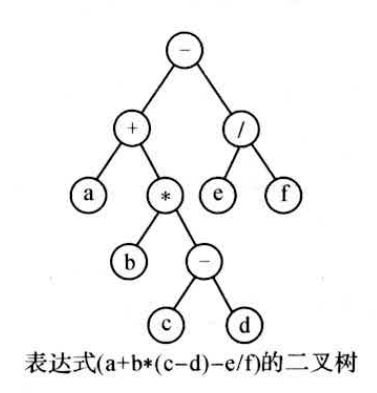

![](https://blog.fivk.cn/usr/uploads/2021/07/1478135364.png)

# 五、二叉树的其他重要操作

除了“遍历”以外，二叉树的其他重要操作还有：建立一颗二叉树、插入一个结点到二叉树中、删除结点或子树等。
</div>

* **1.建立一颗二叉树**

```cpp
void pre_crt(tree &bt)		//按先序次序输入二叉树中结点的值生成
{
	char ch;
	ch=getchar();	//二叉树的单链表存储结构，bt为指向根节点的指针，'$'表示空树
	if(ch!='$')
	{
		bt->new node;		//建立根节点
		bt->data=ch;
		pre_crt(bt->lchild);	//建立左子树
		pre_crt(bt->rchild);	//建立右子树
	}
	else bt=NULL;
}
```

- **2.删除二叉树**

```cpp
void dis(tree &bt)	//删除二叉树
{
	if(bt)
	{
		dis(bt->lchild);	//删除左子树
		dis(bt->rchild);	//删除右子树
		delete bt;		//释放父节点
	}
}
```

- **3.插入一个结点到排序二叉树中**

```cpp
void insert(tree &pb,int n)	//插入一个结点到排序二叉树中
{
	if(pb)
	{
		if(n<bt->data) insert(bt->lchild,n);
		else if(n>bt->data) insert(bt->rchild,n);
	}
	else
	{
		bt=new node;	//新开辟一块空间
		bt->data=n;
		bt->lchild=bt->rchild=NULL;
	}
}
```

- **4.在排序二叉树中查找一个数，找到返回该节点，否则返回NULL**

```cpp
tree findn(tree bt,int n)	//在二叉树中查找一个数，找到返回该节点，否则返回NULL
{
	if(bt)
	{
		if(n<bt->data) findn(bt->lchild,n);
		else if(n>bt->data) find(bt->rchild,n);
		else return bt;
	}
	else return NULL;
}
```

- **5.用嵌套括号表示法输出二叉树**

```cpp
void print(tree bt)		//用嵌套括号法输出二叉树
{
	if(bt)
	{
		cout<<bt->data;
		if(bt->lchild || bt->rchild)
		{
			cout<<'(';
			print(bt->lchild);
			if(bt->rchild) cout<<',';
			print(bt->rchild);
			cout<<')';
		}
	}
}
```

## 补空法创建二叉树与遍历二叉树

补空法是指：如果树的左子树或右子树为空时，则用特殊字符补空，如'#'。然后按照先序遍历的顺序，得到先序遍历序列，再根据序列递归创建二叉树。

算法实现：

如果ch=='#'，bt==NULL，否则创建一个新结点，令bt->data=ch，递归创建bt的左子树，递归创建bt的右子树。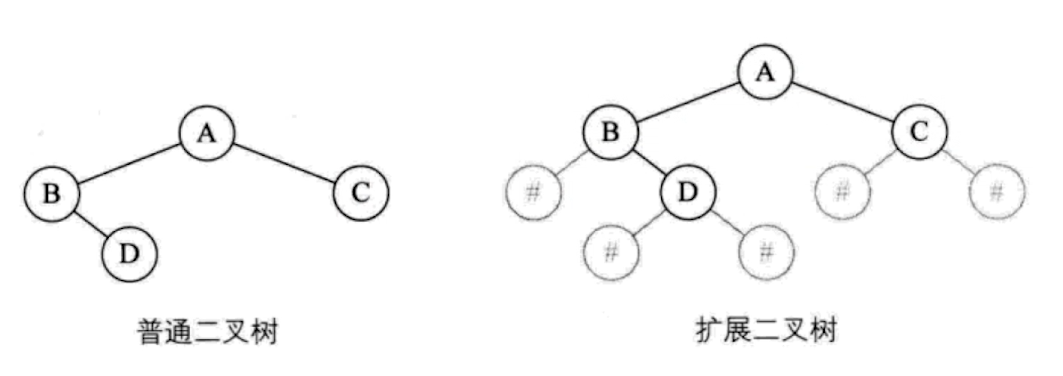

![](https://blog.fivk.cn/usr/uploads/2021/07/1379453709.png)

```cpp
#include<iostream>
#include<cstdlib>
#include<queue>
using namespace std;

//定义二叉树的存储结构
typedef struct node
{
    char data;
    struct node *lchild,*rchild;
}*tree,Node;

//创建二叉树
void CreateTree(tree &bt);

//先序遍历
void preorder(tree bt);

//中序遍历
void inorder(tree bt);

//后序遍历
void postorder(tree bt);

//层序遍历
void LevelTraverse(tree);

int main()
{
    tree mytree;
    cout<<"请按照先序遍历次序输入二叉树结点的值（孩子为空输入#），创建一颗二叉树"<<endl;
    CreateTree(mytree);
    cout<<endl;

cout<<"二叉树先序遍历的结果"<<endl;
    preorder(mytree);
    cout<<endl;

cout<<"二叉树中序遍历的结果"<<endl;
    inorder(mytree);
    cout<<endl;

cout<<"二叉树后序遍历的结果"<<endl;
    postorder(mytree);
    cout<<endl;

cout<<"二叉树层序遍历的结果"<<endl;
    LevelTraverse(mytree);
    cout<<endl;

system("pause");
    return 0;
}

//按先序次序输入，创建二叉树
void CreateTree(tree &bt)
{
    char ch;
    ch=getchar();
    if(ch=='#')
    {
        bt=NULL;
    }else{
        bt=new Node;    //创建一个根结点
        bt->data=ch;
        bt->lchild=NULL;
        bt->rchild=NULL;

CreateTree(bt->lchild);
        CreateTree(bt->rchild);
    }
}

//先序遍历
void preorder(tree bt)
{
    if(bt)
    {
        cout<<bt->data;
        preorder(bt->lchild);
        preorder(bt->rchild);
    }
}

//中序遍历
void inorder(tree bt)
{
    if(bt)
    {
        inorder(bt->lchild);
        cout<<bt->data;
        inorder(bt->rchild);
    }
}

//后序遍历
void postorder(tree bt)
{
    if(bt)
    {
        postorder(bt->lchild);
        postorder(bt->rchild);
        cout<<bt->data;
    }
}

//层序遍历
void LevelTraverse(tree bt)
{
    queue<tree> Q;
    tree p;
    if(bt!=NULL)
    {
        Q.push(bt);
        while(!Q.empty())
        {
            p=Q.front();
            Q.pop();
            cout<<p->data;

if(p->lchild)
                Q.push(p->lchild);
  
            if(p->rchild)
                Q.push(p->rchild);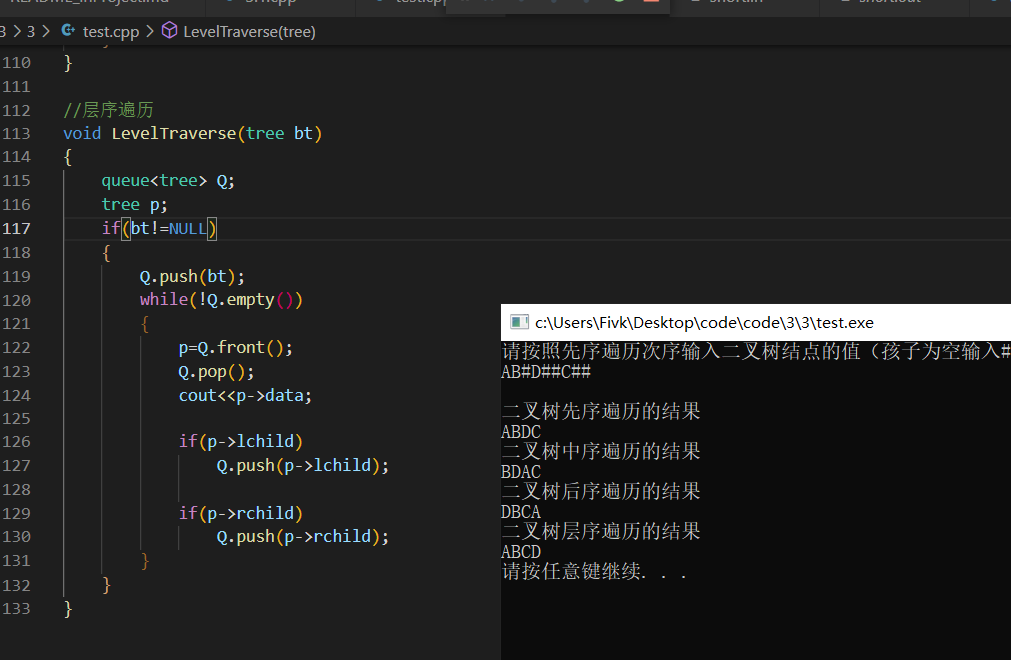
        }
    }
}
```

![运行结束](https://blog.fivk.cn/usr/uploads/2021/07/1974717255.png)

下面我们换个角度考虑这个问题，从二叉树的遍历已经知道，任意一颗二叉树结点的先序序列和中序序列是唯一的。反过来，给定结点的先序序列和中序序列，能否确定一颗二叉树呢？又是否唯一呢？

由定义，二叉树的先序遍历是先访问根节点，再遍历左子树，最后遍历右子树，即在结点的先序序列中，第一个结点必须是根节点，假设为root。再结合中序遍历，因为中序遍历是先遍历左子树，再访问根节点，最后遍历右子树，所以结点root正好把中序序列分成了两部分，root之前应该是左子树上的结点，root之后应该是右子树的结点。依次类推，便可递归得到整颗二叉树。

结论：

已知先序序列和中序序列可以确定出二叉树；

已知中序序列和后序序列也可以确定出二叉树；

</div>

但，已知前序序列和后序序列却不能确定出二叉树；为什么？举出3个结点的反例。

假如：已知结点的先序序列为ABCDEFG，中序序列为：CBEDAFG。构造出二叉树，过程见图：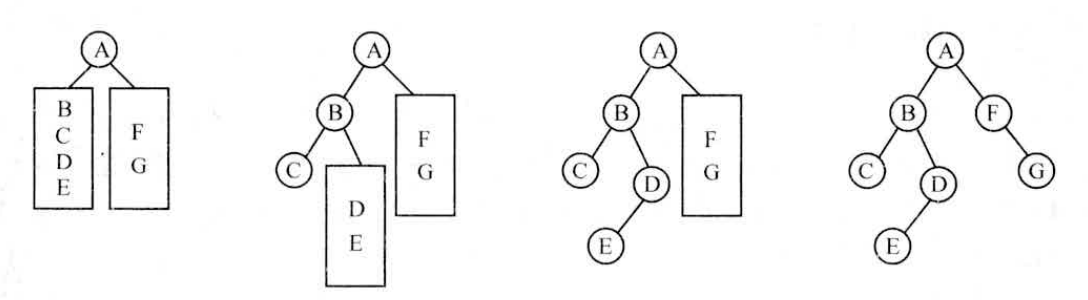

![](https://blog.fivk.cn/usr/uploads/2021/07/1554414151.png)

**例 3.4 求后序遍历**

【问题描述】

输入一颗二叉树的先序和中序遍历序列，输出其后序列遍历序列。

</div>

【输入格式】

输入文件为tree.in，共两行，第1行一个字符串，表示树的先序遍历，第2行一个字符串，表示树的中序遍历。树的结点一律用小写字母表示。

【输出格式】

输出文件为tree.out，仅一行，表示树的后序遍历序列。

【输入样例】

```in
abdec
dbeac
```

【输出样例】

```out
debca
```

![](https://blog.fivk.cn/usr/uploads/2021/07/2736930442.png)

```cpp
#include<cstring>
#include<iostream>
#include<cstdio>
using namespace std;
string s1,s2;

void calc(int l1,int r1,int l2,int r2)
{
    int m=s2.find(s1[l1]);
    if(m>l2) calc(l1+1,l1+m-12,12,m-1);
    if(m<r2) calc(l1+m-12+1,r1,m+1,r2);
    cout<<s1[l1];
}

int main()
{
    cin>>s1>>s2;
    calc(0,s1.length()-1,0,s2.length()-1);
    cout<<endl;
    system("pause");
    return 0;
}
```

**例 3.5 扩展二叉树**

【问题描述】

由于先序、中序、后序序列中的任意一个都不能唯一确定一颗二叉树，所以对二叉树做如下处理，将二叉树的空结点用“·”补齐，如图所示。我们把这样处理后的二叉树称为原二叉树的扩展二叉树，扩展二叉树的先序和后序序列能唯一确定其二叉树。

![](https://blog.fivk.cn/usr/uploads/2021/07/3311886758.png)

现给出扩展二叉树的先序序列，要求输出其中序序列和后序序列。

</div>

【输入样例】

```in
ABD..EF..G..C..
```

【输出样例】

```out
DBFEGAC
DFGEBCA
```

现在看起来就真的感觉太简单啦，哈哈哈哈哈

```cpp
#include<iostream>
#include<cstdlib>
#include<queue>
using namespace std;

typedef struct node
{
    char data;
    struct node *lchild,*rchild;
}Node,*tree;

//前序插入
void Insert(tree &bt)
{
    char ch;
    cin>>ch;
    if(ch!='.')
    {
        bt=new node;
        bt->data=ch;
        bt->lchild=bt->rchild=NULL;

Insert(bt->lchild);
        Insert(bt->rchild);

}else{
        bt=NULL;
    }
}

//前序遍历
void print1(tree bt)
{
    if(bt)
    {
        print1(bt->lchild);
        cout<<bt->data;
        print1(bt->rchild);
    }
}

//后序遍历
void print2(tree bt)
{
    if(bt)
    {
        print2(bt->lchild);
        print2(bt->rchild);
        cout<<bt->data;
    }
}

//层序遍历
void print3(tree bt)
{
    if(bt)
    {
        tree p;
        queue<tree> Q;
        Q.push(bt);

while(Q.size())
        {
            p=Q.front();
            Q.pop();

cout<<p->data;

if(p->lchild)
                Q.push(p->lchild);

if(p->rchild)
                Q.push(p->rchild);
        }
    }
}

int main()
{
    tree mybt;
    Insert(mybt);
    print1(mybt);
    cout<<endl;

print2(mybt);
    cout<<endl;

print3(mybt);
    cout<<endl;

system("pause");
    return 0;
}
```

# 六、普通树转换成二叉树

由于二叉树是有序的，而且操作和应用更广泛，所以在实际使用时，我们经常把普通树转换成为叉树进行操作。如何转换呢？一般方法如下：

1. 将树中每个结点除了最左边的一个分支保留外，其余分支都去掉。
2. 从最左边结点开始画一条线，把同一层上的兄弟结点都链接起来。
3. 以整颗树的根结点为轴心，将整颗树顺时针大致旋转45度。

把图所示的普通树转换成二叉树的过程如图所示：

![](https://blog.fivk.cn/usr/uploads/2021/07/2457561060.png)

同样我们可以把森林也转换成二叉树处理，假设$F$={$T_1,T_2,...,T_m$}是森林，则可按如下规则转换成一颗二叉树$B$={$root,lb,rb$}。

1. 若F为空，即m=0，则B为空树。
2. 若F为非空，即m!=0，则B的根root即为森立中第一颗树的根$root(T_1)$;B的左子树lb是从$T_1$中根节点的子树森林$F_1=${$T_{11},T_{12},T_{13},...,T_{1m}$}转换而成的二叉树；其右子树rb是从森立$F^{'}$={$T_2,T_3,...,T_m$}转换而成的二叉树。

# 七、树的统计数问题

具有n个结点的不同形态的二叉树有多少棵？具有n个结点的不同形态的树有多少棵？首先了解两个概念，“相似二叉树”是指两者不仅相似，而且所有对应结点上的数据元素均相同。二叉树的计数问题就是讨论具有n个结点、互不相似的二叉树的数目$A_n$。

在n很小时，很容易得出，$A_0=1,A_1=1,A_2=2,A_3=5$。

![](https://blog.fivk.cn/usr/uploads/2021/07/1049708352.png)

一般情况，一棵具有k(k>1)个结点的二叉树可以看成是由一个根结点、一颗具有i个结点的左子树和一颗具有i个结点的左子树和一颗具有k-i-1个结点的右子树，其中0<=i<=k-1。

由此不难得出下列递归公式：

$A[K]=\sum_{i=0}^{k-1}A[i]*A[k-1-i]$

其中$A[0]=1,A[1]=1$。

这个递推公式，我们就能够想到[Catalan数](https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746?fromtitle=Catalan%E6%95%B0&fromid=7767308&fr=aladdin)，这就是[Catalan数](https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746?fromtitle=Catalan%E6%95%B0&fromid=7767308&fr=aladdin)的形式之一。我们可以利用生成函数讨论这个递归公式，得出[Catalan数](https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746?fromtitle=Catalan%E6%95%B0&fromid=7767308&fr=aladdin)的另一个形式：

$A[K]=C_{2k}^k*\frac{1}{K+1}$

类推到具有K个结点、互不相似的多叉树的数目$T_k$，由于树可以转换成二叉树且转换之后的根节点没有右儿子，所以，可以推出：$T_k=A[K-1]$。

**例 3.6 二叉树计数**

【题目描述】

由n个结点可组成多少个不同形态的二叉树？

</div>

【输入格式】

一行，一个正整数n。

【输出格式】

不同的二叉树的个数。

【样例输入】

```in
2
```

【样例输出】

```out
2
```

【数据规模】

保证 40%的数据n<=35

保证 100%的数据n<=5000

我们记由k个结点构成的不同形态的二叉树数目A[K]。对于一颗二叉树，它必定是由根、左子树和右子树构成（其中左子树与右子树可为空树）。

我们由$A[K]=C_{2k}^k*\frac{1}{K+1}$这个通向就让我们有能力应付题目的数据范围了，剩下的工作就是高精度乘与高精度除了。

$A[K]=C_{2k}^k*\frac{1}{K+1}$

$=\frac{(2k)!}{k!*k!*(k+1)}$

$=\frac{(k+2)*(k+3)*...*(2k)}{2*3*...*k}$

高精度乘法和高高精度除技巧：

算组合时，我们可以边乘边除，这样可以极大地提高运算效率。这种算法最后能得到70分；更强的优化是，直接将乘数和除数分解质因数，同时统计各个质因数个数，最后将这些质因数相乘即可。这也是本题的标准算法；最后有一种基于位移的高精度乘法，这是在乘数过多时使用的，感兴趣的请自行搜索相关资料。

最后修改：2021 年 09 月 12 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

【数据结构】二叉树

Fivk • 2021 年 07 月 13 日

# 一、二叉树基本概念

![](https://blog.fivk.cn/usr/uploads/2021/07/1734372890.png)

# 二、二叉树的性质

$2^0+2^1+2^2+2^3+...+2^{k-1}=2^k-1$

![](https://blog.fivk.cn/usr/uploads/2021/07/3513745431.png)

$n-1=n_1+n_2$        (式子2)
由式子1和式子2得到:$n_0=n_2+1$

【性质5】对于一棵n个结点的完全二叉树,对任一个结点(编号为i),有:

![](https://blog.fivk.cn/usr/uploads/2021/07/2824171434.png)

# 三、二叉树的存储结构

> （1）**链式存储结构**：即单链表结构或双链表结构（同树）。数据结构修改如下：

```cpp
typedef struct node;
typedef node* tree;
struct node
{
	char data;
	tree lchild,rchild;
};
tree bt;
```

或

```cpp
typedef struct node;
typedef node* tree;
struct node
{
	char data;
	tree lchild,rchild,father;
};
tree bt;
```

如图A的一颗二叉树用单链表就可以表示成如图B的形式：

![](https://blog.fivk.cn/usr/uploads/2021/07/1478096122.png)

> （2）**顺序储存结构**：即几个数组加一个指针变量。数据结构如下：

```cpp
const int n=10;
char data[n];
char lchild[n];
char rchild[n];
int bt;			//根结点指针
```

![](https://blog.fivk.cn/usr/uploads/2021/07/1985862166.png)

数据结构定义如下：

```cpp
char data[9]={'a','+','b','/','c','*','d','-','e'};
int lchild[9]={0,1,0,3,0,2,0,7,0};
int rchild[9]={0,4,0,5,0,8,0,9,0};
int bt;			//结点点指针，初值=6,指向'*'
```

二叉树的操作：最重要的是遍历二叉树，但基础又是建一颗二叉树、插入一个结点到二叉树中、删除结点或子树等。
</div>

**例 3.3 医院设置**

【问题描述】

![](https://blog.fivk.cn/usr/uploads/2021/07/54869262.png)

</div>

【输入格式】

【输出格式】

输出文件为hospital.out，该文件只有一个整数，表示最小距离和。

【输入格式】

```in
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
```

【输出样例】

```out
8
```

cin>>n;

for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            g[i][j]=1000000;

for(i=1;i<=n;i++)   //读入、初始化
    {
        g[i][i]=0;
        cin>>a[i]>>l>>r;
        if(l>0) g[i][l]=g[l][i]=1;
        if(r>0) g[i][r]=g[r][i]=1;
    }

for(i=1;i<=n;i++)
    {
        total=0;
        for(j=1;j<=n;j++)
            total+=g[i][j]*a[j];
        if(total<min) min=total;
    }

cout<<min<<endl;

fclose(stdin);
    fclose(stdout);

system("pause");
    return 0;
}
```

后记：

【问题描述】

</div>

【输入格式】

仅1行，一个实数（保留两位小数），表示从s到t的最短路径长度。

```in
5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5
```

```out
3.41
```

```cpp
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;

int a[101][3];
double f[101][101];

int main()
{

int i,j,k,total,min;
    int n,m,x,y,s,t;

memset(f,0x7f,sizeof(f));

cin>>n;

for(i=1;i<=n;i++)
        cin>>a[i][1]>>a[i][2];
    cin>>m;

for(i=1;i<=m;i++)
    {
        cin>>x>>y;
        f[x][y]=f[y][x]=sqrt(pow(double(a[x][1]-a[y][1]),2)+pow(double(a[x][2]-a[y][2]),2));
    }

cin>>s>>t;

for(k=1;k<=n;k++)
        for(i=1;i<=n;i++)
            if(k!=i)
            for(j=1;j<=n;j++)
            if(j!=i && j!=k && f[i][j]>f[k][j]+f[i][k])
            f[i][j]=f[k][j]+f[i][k];

printf("%.2lf\n",f[s][t]);

return 0;
}
```

# 四、遍历二叉树

![](https://blog.fivk.cn/usr/uploads/2021/07/3775628437.png)

> （一）先序遍历的操作定义如下

若二叉树为空，则空操作返回，否则：

1. 访问根结点
2. 先序遍历左子树
3. 先序遍历右子树

先序遍历树结果为：124753689

数据结构如下：

> （二）中序遍历的操作定义如下：

若二叉树为空，则空操作返回，否则：

1. 中序遍历左子树
2. 访问根结点
3. 中序遍历右子树

数据结构如下：

> （三）后序遍历的操作定义如下：

若二叉树为空，则空操作返回，否则：

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根节点

后序遍历结果为：745289631

> （四）层序遍历的操作定义如下：

若二叉树为空，则空操作返回，否则：

1. 从树的第一层（也就是根结点）访问
2. 从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。

如下图所示，遍历的顺序为：ABCDEFGHL

![](https://blog.fivk.cn/usr/uploads/2021/07/3482429990.png)

cout<<p->data<<"  ";
		fi(p->lchild)
			Q.push(p->lchild);
		if(p->rchild)
			Q.push(p->rchild);
	}
	return true;
}
```

当然我们还可以改用栈实现的非递归过程，这里我们就不探究了。

</div>

* $-+a*b-cd/rf$（前缀表式，波兰式）
* $a+b*c-d-e/f$（中缀表达）
* $abcd-*+ef/-$（后缀表示，逆波兰式）

![](https://blog.fivk.cn/usr/uploads/2021/07/1478135364.png)

# 五、二叉树的其他重要操作

除了“遍历”以外，二叉树的其他重要操作还有：建立一颗二叉树、插入一个结点到二叉树中、删除结点或子树等。
</div>

* **1.建立一颗二叉树**

- **2.删除二叉树**

```cpp
void dis(tree &bt)	//删除二叉树
{
	if(bt)
	{
		dis(bt->lchild);	//删除左子树
		dis(bt->rchild);	//删除右子树
		delete bt;		//释放父节点
	}
}
```

- **3.插入一个结点到排序二叉树中**

- **4.在排序二叉树中查找一个数，找到返回该节点，否则返回NULL**

- **5.用嵌套括号表示法输出二叉树**

## 补空法创建二叉树与遍历二叉树

算法实现：

如果ch=='#'，bt==NULL，否则创建一个新结点，令bt->data=ch，递归创建bt的左子树，递归创建bt的右子树。

![](https://blog.fivk.cn/usr/uploads/2021/07/1379453709.png)

```cpp
#include<iostream>
#include<cstdlib>
#include<queue>
using namespace std;

//定义二叉树的存储结构
typedef struct node
{
    char data;
    struct node *lchild,*rchild;
}*tree,Node;

//创建二叉树
void CreateTree(tree &bt);

//先序遍历
void preorder(tree bt);

//中序遍历
void inorder(tree bt);

//后序遍历
void postorder(tree bt);

//层序遍历
void LevelTraverse(tree);

int main()
{
    tree mytree;
    cout<<"请按照先序遍历次序输入二叉树结点的值（孩子为空输入#），创建一颗二叉树"<<endl;
    CreateTree(mytree);
    cout<<endl;

cout<<"二叉树先序遍历的结果"<<endl;
    preorder(mytree);
    cout<<endl;

cout<<"二叉树中序遍历的结果"<<endl;
    inorder(mytree);
    cout<<endl;

cout<<"二叉树后序遍历的结果"<<endl;
    postorder(mytree);
    cout<<endl;

cout<<"二叉树层序遍历的结果"<<endl;
    LevelTraverse(mytree);
    cout<<endl;

system("pause");
    return 0;
}

CreateTree(bt->lchild);
        CreateTree(bt->rchild);
    }
}

//先序遍历
void preorder(tree bt)
{
    if(bt)
    {
        cout<<bt->data;
        preorder(bt->lchild);
        preorder(bt->rchild);
    }
}

//中序遍历
void inorder(tree bt)
{
    if(bt)
    {
        inorder(bt->lchild);
        cout<<bt->data;
        inorder(bt->rchild);
    }
}

//后序遍历
void postorder(tree bt)
{
    if(bt)
    {
        postorder(bt->lchild);
        postorder(bt->rchild);
        cout<<bt->data;
    }
}

if(p->lchild)
                Q.push(p->lchild);
  
            if(p->rchild)
                Q.push(p->rchild);
        }
    }
}
```

![运行结束](https://blog.fivk.cn/usr/uploads/2021/07/1974717255.png)

结论：

已知先序序列和中序序列可以确定出二叉树；

已知中序序列和后序序列也可以确定出二叉树；

</div>

但，已知前序序列和后序序列却不能确定出二叉树；为什么？举出3个结点的反例。

假如：已知结点的先序序列为ABCDEFG，中序序列为：CBEDAFG。构造出二叉树，过程见图：

![](https://blog.fivk.cn/usr/uploads/2021/07/1554414151.png)

**例 3.4 求后序遍历**

【问题描述】

输入一颗二叉树的先序和中序遍历序列，输出其后序列遍历序列。

</div>

【输入格式】

输入文件为tree.in，共两行，第1行一个字符串，表示树的先序遍历，第2行一个字符串，表示树的中序遍历。树的结点一律用小写字母表示。

【输出格式】

输出文件为tree.out，仅一行，表示树的后序遍历序列。

【输入样例】

```in
abdec
dbeac
```

【输出样例】

```out
debca
```

![](https://blog.fivk.cn/usr/uploads/2021/07/2736930442.png)

```cpp
#include<cstring>
#include<iostream>
#include<cstdio>
using namespace std;
string s1,s2;

void calc(int l1,int r1,int l2,int r2)
{
    int m=s2.find(s1[l1]);
    if(m>l2) calc(l1+1,l1+m-12,12,m-1);
    if(m<r2) calc(l1+m-12+1,r1,m+1,r2);
    cout<<s1[l1];
}

int main()
{
    cin>>s1>>s2;
    calc(0,s1.length()-1,0,s2.length()-1);
    cout<<endl;
    system("pause");
    return 0;
}
```

**例 3.5 扩展二叉树**

【问题描述】

![](https://blog.fivk.cn/usr/uploads/2021/07/3311886758.png)

现给出扩展二叉树的先序序列，要求输出其中序序列和后序序列。

</div>

【输入样例】

```in
ABD..EF..G..C..
```

【输出样例】

```out
DBFEGAC
DFGEBCA
```

现在看起来就真的感觉太简单啦，哈哈哈哈哈

```cpp
#include<iostream>
#include<cstdlib>
#include<queue>
using namespace std;

typedef struct node
{
    char data;
    struct node *lchild,*rchild;
}Node,*tree;

//前序插入
void Insert(tree &bt)
{
    char ch;
    cin>>ch;
    if(ch!='.')
    {
        bt=new node;
        bt->data=ch;
        bt->lchild=bt->rchild=NULL;

Insert(bt->lchild);
        Insert(bt->rchild);

}else{
        bt=NULL;
    }
}

//前序遍历
void print1(tree bt)
{
    if(bt)
    {
        print1(bt->lchild);
        cout<<bt->data;
        print1(bt->rchild);
    }
}

//后序遍历
void print2(tree bt)
{
    if(bt)
    {
        print2(bt->lchild);
        print2(bt->rchild);
        cout<<bt->data;
    }
}

//层序遍历
void print3(tree bt)
{
    if(bt)
    {
        tree p;
        queue<tree> Q;
        Q.push(bt);

while(Q.size())
        {
            p=Q.front();
            Q.pop();

cout<<p->data;

if(p->lchild)
                Q.push(p->lchild);

if(p->rchild)
                Q.push(p->rchild);
        }
    }
}

int main()
{
    tree mybt;
    Insert(mybt);
    print1(mybt);
    cout<<endl;

print2(mybt);
    cout<<endl;

print3(mybt);
    cout<<endl;

system("pause");
    return 0;
}
```

# 六、普通树转换成二叉树

由于二叉树是有序的，而且操作和应用更广泛，所以在实际使用时，我们经常把普通树转换成为叉树进行操作。如何转换呢？一般方法如下：

把图所示的普通树转换成二叉树的过程如图所示：

![](https://blog.fivk.cn/usr/uploads/2021/07/2457561060.png)

同样我们可以把森林也转换成二叉树处理，假设$F$={$T_1,T_2,...,T_m$}是森林，则可按如下规则转换成一颗二叉树$B$={$root,lb,rb$}。

# 七、树的统计数问题

在n很小时，很容易得出，$A_0=1,A_1=1,A_2=2,A_3=5$。

![](https://blog.fivk.cn/usr/uploads/2021/07/1049708352.png)

由此不难得出下列递归公式：

$A[K]=\sum_{i=0}^{k-1}A[i]*A[k-1-i]$

其中$A[0]=1,A[1]=1$。

$A[K]=C_{2k}^k*\frac{1}{K+1}$

类推到具有K个结点、互不相似的多叉树的数目$T_k$，由于树可以转换成二叉树且转换之后的根节点没有右儿子，所以，可以推出：$T_k=A[K-1]$。

**例 3.6 二叉树计数**

【题目描述】

由n个结点可组成多少个不同形态的二叉树？

</div>

【输入格式】

一行，一个正整数n。

【输出格式】

不同的二叉树的个数。

【样例输入】

```in
2
```

【样例输出】

```out
2
```

【数据规模】

保证 40%的数据n<=35

保证 100%的数据n<=5000

我们记由k个结点构成的不同形态的二叉树数目A[K]。对于一颗二叉树，它必定是由根、左子树和右子树构成（其中左子树与右子树可为空树）。

我们由$A[K]=C_{2k}^k*\frac{1}{K+1}$这个通向就让我们有能力应付题目的数据范围了，剩下的工作就是高精度乘与高精度除了。

$A[K]=C_{2k}^k*\frac{1}{K+1}$

$=\frac{(2k)!}{k!*k!*(k+1)}$

$=\frac{(k+2)*(k+3)*...*(2k)}{2*3*...*k}$

高精度乘法和高高精度除技巧：

【数据结构】二叉树

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

【Fivk】文章归档

回忆刚入天柱二中的我

【Java】集合之HashTable

HBase 入门：理解其特性并使用 Java API 进行操作

【开发技巧】字符串判断为空或者非空

【踩坑日志】端口被占用导致Tomcat报错或者springboot启动报错

【相册图片】20岁生日

【数据结构】二叉树

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【数据结构】二叉树

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款