【算法基础】更加简单通用的二分查找模板

博主： Fivk
发布时间：2023 年 09 月 13 日
520 次浏览
1004字数
分类：算法基础

# 一、模板示范

闫而总之，只要所要寻找的数组能够满足某一条件而被分成两边，就能进行二分，这边我们就拿有序数组的二分来做例子；
假设目前有这么一组数据:1 2 2 3 3 4 下标从0开始

![](https://blog.fivk.cn/usr/uploads/2023/09/469866690.png)

假设此时的情景为，需要我们找到第一个≥3的数字，**试想一下，如果能把整个区间分了两半，左边是<3的区间，右边是≥3的区间** 如图: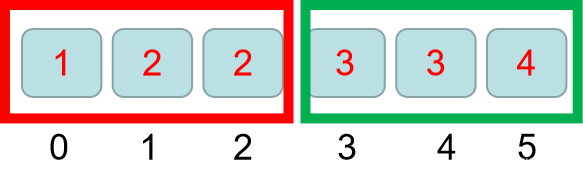

![](https://blog.fivk.cn/usr/uploads/2023/09/3388873862.png)

**那么右区间的第一个点，就是我们找到的符合≥3的第一个数字**,将区间分为两半，是不是非常清晰！
我先给出代码实现(不要害怕 马上就能见证奇迹)

```cpp
#include<iostream>
using namespace std;

int main() {
	int a[6]={1,2,2,3,3,4};
	int l=-1,r=6; //定义两个指针
	while (l+1!=r) {
		int mid=l+r>>1; //(相当于(l+r)/2)
		if (a[mid] < 3) l=mid; //或者if(a[mid]>=3) r=mid;
		else r=mid;		   // else l=mid;
	}
	cout<<"第一个3所在的下标为  "<<r<<endl;
	return 0;
}
```

```cout
返回的结果为:第一个3所在的下标为  3
```

最后二分的结果就是下面这个图，是我们想要的样子！
然后因为我们要找到的是第一个>=3的数字，所以就取 r 也就是>=3区间的第一个数字；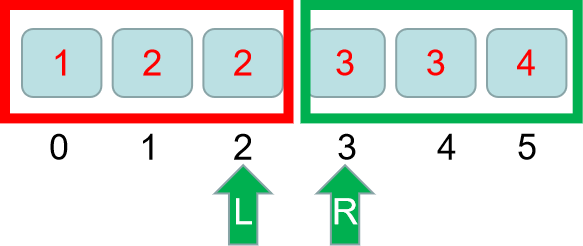

![](https://blog.fivk.cn/usr/uploads/2023/09/1687389162.png)

# 二、模板

对于一个有序数组,假设下标为0,1,2,3…,n-1;总共n个数字
那么模板为

```cpp
int L=-1,R=n;
while(L+1!=R)
{
	int mid=L+R>>1;
	if(check()) L=mid;
	else R=mid;
	//最后根据你所分左右两边区间的结果
	//选取L或者R作为结果
}
```

# 三、细节说明

## 为什么L的初始值为-1，R的初始值为N

> 首先，如果二分本来就没有结果：比如对于本文例题 1 2 2 3 3 4，，如果你要寻找第一个 **>=5** 的数，你会发现，整个过程都在执行**L=mid**，最后得到的结果中,**R是等于下标6的，他明显这个时候是越界的，说明我们找不到要寻找的数字**，而如果我们一开始将**R赋值为n-1，也就是赋值为下标5的时候**，他返回的R是5，**是没有越界的，被我们当成了答案，但其实这时候我们的二分是没有答案的,就发生了错误**；

> 其次，L最小值为-1，R最小值只能取到1，因为L+1！=R为循环结束条件，R最大值为N,同理则L的最大值为N-2，则（L+R）/2的取值范围是 [0,N)，mid的值始终位于0到N的左闭右开区间里面,不会发生越界的错误；

## 为什么循环结束的条件是while(L+1!=R)?

之前学过二分的小伙伴可能会发现，之前学的二分，他循环结束的条件是**while(L<R)**

而这边给出的循环条件是**while(L+1!=R)** 其实，就是当L和R相邻的时候，循环就结束，而原本的**while(L<R)**

是当**两区间重合**以后，循环才结束，所以之前我们需要判断对**mid**进行加一或者减一的操作，而且因为区间重合的问题，最后返回的L、R还要再进行判断，而这边的这个二分，因为区间反回的是不重合的两区间，**只有L=mid和R=mid这两种情况，最后根据需要返回L或者R；**

## 不会陷入死循环

对于比较奇葩的情况，比如数组大小为1或者2

比如int a[1],b[2];

由于我们是while(L+1!=R)结束循环，也就是当L和R相邻的时候结束条件

**对于a[1],他的下标为0 此时L=-1，R=n也就是1**

**对于b[2],他的下标为0,1 此时L=-1，R=n也就是2**

所以无论何种情况，初始的L+1始终小于R，历经循环后最终L和R相邻，不会出现一开始L就和R重合等情况导致出现while(L+1!=R)循环不能结束的情况

# 最后

我们就能够通过二分得到不重合的两区间，而且只需要L=mid和R=mid，不需要考虑L=mid+1，R=mid-1的情况且记得一开始对于一个下标为0,1,2…n-1的数组，指针L要赋值为-1，指针R要赋值为n，那么你就学会了最后我给出y总基础算法中的二分例题

**AcWing.789-数的范围**的这题的关于这个二分方法的代码实现

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-0839ba739a545fdd7249f5ebd3b347c946" aria-expanded="true"><div class="accordion-toggle"><span style="">【题目点击展开】</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-0839ba739a545fdd7249f5ebd3b347c946" class="collapse collapse-content"><p></p>

给定一个按照升序排列的长度为 $n$的整数数组，以及$q$个查询。
对于每个查询，返回一个元素 $k$的起始位置和终止位置（位置从$0$开始计数）。
如果数组中不存在该元素，则返回 `-1 -1`。

**输入格式**
第一行包含整数$n$ 和 $q$，表示数组长度和询问个数。

第二行包含 $n$ 个整数（均在 $1∼10000$范围内），表示完整数组。

接下来 $q$ 行，每行包含一个整数 $k$，表示一个询问元素。

**输出格式**
共 $q$ 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 `-1 -1`。
**数据范围**
$1≤n≤100000$
$1≤q≤10000$
$1≤k≤10000$
**输入样例：**

```bash
6 3
1 2 2 3 3 4
3
4
5
```

**输出样例：**

```bash
3 4
5 5
-1 -1
```

```cpp
#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int a[N];

int main() {
	int n, q, k;

cin >> n >> q;

for (int i = 0; i < n; i ++) {
		cin >> a[i];
	}

while (q --) {
		cin >> k;
		// 寻找第一个k出现的下标，我这边让二分的边界定为 左边为<k 右边>=k 则所求为r 
		int l = -1, r = n;

while (l + 1 != r) {
			int mid = l + r >> 1;
			if (a[mid] >= k) r = mid;
			else l = mid; 
		}

//此时得到的r是第一个>=k的坐标
		if (a[r] != k) {
			cout << "-1 -1" << endl;
		} else {
			cout << r << ' ';

// 寻找最后出现k的下标，我这边让二分的边界定为 左边界 <= k,右边界 > k，则所求为l
			l = -1, r = n;
			while (l + 1 != r) {
				int mid = l + r >> 1;
				if (a[mid] <= k) l = mid;
				else r = mid;
			}

cout << l << endl;
		}
	}

return 0;
}
```

附上相关学习视频：[https://www.bilibili.com/video/BV1d54y1q7k7](https://www.bilibili.com/video/BV1d54y1q7k7)

最后修改：2023 年 12 月 06 日

如果觉得我的文章对你有用，请随意赞赏

【算法基础】更加简单通用的二分查找模板

Fivk • 2023 年 09 月 13 日

# 一、模板示范

![](https://blog.fivk.cn/usr/uploads/2023/09/469866690.png)

假设此时的情景为，需要我们找到第一个≥3的数字，**试想一下，如果能把整个区间分了两半，左边是<3的区间，右边是≥3的区间** 如图:

![](https://blog.fivk.cn/usr/uploads/2023/09/3388873862.png)

**那么右区间的第一个点，就是我们找到的符合≥3的第一个数字**,将区间分为两半，是不是非常清晰！
我先给出代码实现(不要害怕 马上就能见证奇迹)

```cpp
#include<iostream>
using namespace std;

```cout
返回的结果为:第一个3所在的下标为  3
```

最后二分的结果就是下面这个图，是我们想要的样子！
然后因为我们要找到的是第一个>=3的数字，所以就取 r 也就是>=3区间的第一个数字；

![](https://blog.fivk.cn/usr/uploads/2023/09/1687389162.png)

# 二、模板

对于一个有序数组,假设下标为0,1,2,3…,n-1;总共n个数字
那么模板为

```cpp
int L=-1,R=n;
while(L+1!=R)
{
	int mid=L+R>>1;
	if(check()) L=mid;
	else R=mid;
	//最后根据你所分左右两边区间的结果
	//选取L或者R作为结果
}
```

# 三、细节说明

## 为什么L的初始值为-1，R的初始值为N

## 为什么循环结束的条件是while(L+1!=R)?

之前学过二分的小伙伴可能会发现，之前学的二分，他循环结束的条件是**while(L<R)**

而这边给出的循环条件是**while(L+1!=R)** 其实，就是当L和R相邻的时候，循环就结束，而原本的**while(L<R)**

## 不会陷入死循环

对于比较奇葩的情况，比如数组大小为1或者2

比如int a[1],b[2];

由于我们是while(L+1!=R)结束循环，也就是当L和R相邻的时候结束条件

**对于a[1],他的下标为0 此时L=-1，R=n也就是1**

**对于b[2],他的下标为0,1 此时L=-1，R=n也就是2**

所以无论何种情况，初始的L+1始终小于R，历经循环后最终L和R相邻，不会出现一开始L就和R重合等情况导致出现while(L+1!=R)循环不能结束的情况

# 最后

**AcWing.789-数的范围**的这题的关于这个二分方法的代码实现

**输入格式**
第一行包含整数$n$ 和 $q$，表示数组长度和询问个数。

第二行包含 $n$ 个整数（均在 $1∼10000$范围内），表示完整数组。

接下来 $q$ 行，每行包含一个整数 $k$，表示一个询问元素。

**输出格式**
共 $q$ 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 `-1 -1`。
**数据范围**
$1≤n≤100000$
$1≤q≤10000$
$1≤k≤10000$
**输入样例：**

```bash
6 3
1 2 2 3 3 4
3
4
5
```

**输出样例：**

```bash
3 4
5 5
-1 -1
```

```cpp
#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int a[N];

int main() {
	int n, q, k;

cin >> n >> q;

for (int i = 0; i < n; i ++) {
		cin >> a[i];
	}

while (q --) {
		cin >> k;
		// 寻找第一个k出现的下标，我这边让二分的边界定为 左边为<k 右边>=k 则所求为r 
		int l = -1, r = n;

while (l + 1 != r) {
			int mid = l + r >> 1;
			if (a[mid] >= k) r = mid;
			else l = mid; 
		}

//此时得到的r是第一个>=k的坐标
		if (a[r] != k) {
			cout << "-1 -1" << endl;
		} else {
			cout << r << ' ';

cout << l << endl;
		}
	}

return 0;
}
```

附上相关学习视频：[https://www.bilibili.com/video/BV1d54y1q7k7](https://www.bilibili.com/video/BV1d54y1q7k7)

【算法基础】更加简单通用的二分查找模板

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

这是好东西

【Fivk】文章归档

【C】预处理

数据没了

【C++】STL常用容器_stack容器

【python】数据分析模型

闲来无事，不如有事。

【算法基础】更加简单通用的二分查找模板