【算法基础】分治算法

博主： Fivk
发布时间：2021 年 05 月 08 日
955 次浏览
暂无评论
4037字数
分类：算法基础

所谓分治就是指分而治之，即将较大规模的问题分解成几个较小规模的问题，通过对较小规模问题的求解达到对整个问题的求解。当我们将问题分解成两个较小问题求解时的分治法称之为二分法。

你们玩过猜数字的游戏吗？你的朋友心想一个1000以内的正整数，你可以给出一个数字x，你的朋友只要回答“比x大”或者“比x小”或者“猜中”，你能保证在10次内猜中吗？运气好只要一次就猜中。

gep开始猜测是1到1000之间，你可以先才500，运气好可以一次猜中，如果答案比500大，显然答案不可能在500之间，下一次猜测的区间变成501到1000，如果答案比500小，那答案不可能在500到1000之间，下一次猜测的区间变为1到499。只要每次猜测区间的中间点，这样就可以把猜测区间缩小一半。由于 $\frac{1000}{2^{10}}$$<$ 1 因此不超过10次询问区间就可以缩小为1，答案就会猜中了，这就是二分的基本思想。

每一次使得可选的范围缩小一半，最终使得范围缩小为一个数，从而得出答案。假设问范围是1到n，根据 $\frac{n}{2^{x}}$$\leq$ 1 得 x $\geq$ $\log_2{n}$ ，所以我们只需要问O($log{n}$) 次就能知道答案了。

需要注意的是使用二分法有一个重要的前提，就是有序性，下面通过几个例子来体会二分法的应用。

# 经典案例

## 例1：找数

描述：

给一个长度为n的单调递增的正整数序列，即序列中每一个数都比前一个数大。有m个询问，每次询问一个x，问序列中最后一个小于等于x的数是什么？

**输入：**

第一行两个整数n,m。

接下来一行n个数，表示这个序列。

接下来m行每行一个数，表示一个询问。

**输出：**

输出共m行，表示序列中最后一个小于等于x的数是什么。假设没有，则输出-1。

</div>

【输入样例】

```输入样例
5 3
1 2 3 4 6
5
1 
3
```

【输出样例】

```输出样例
4
1
3
```

我们用Left表示询问的左边区间，用Right表示询问区间的有边界，[Left,Right]组成询问区间。一开始Left=1，Right=n；我们可以把原始序列的左边想象成若干个无穷小的数，把序列的右边想象成无穷大的数，这样比较好理解。序列已经按照升序排好，保证了二分的有序性。

**每一次二分，我们这样来做：**

1. 取区间中间值Mid=(Left+Right)/2;
2. 判断Mid与x的关系，如果a[Mid]>x,由于序列是升序排列，所以区间[Mid,Right]都可以被排除，修改右边界Right=Mid-1;
3. 如果a[Mid] $\leq$ x修改左边界 Left=Mid+1;

**重复执行二分法操作直到Left>Right。**

下面我们来分析答案的情况。<span style="color:#A52A2A">循环结束</span>示意图：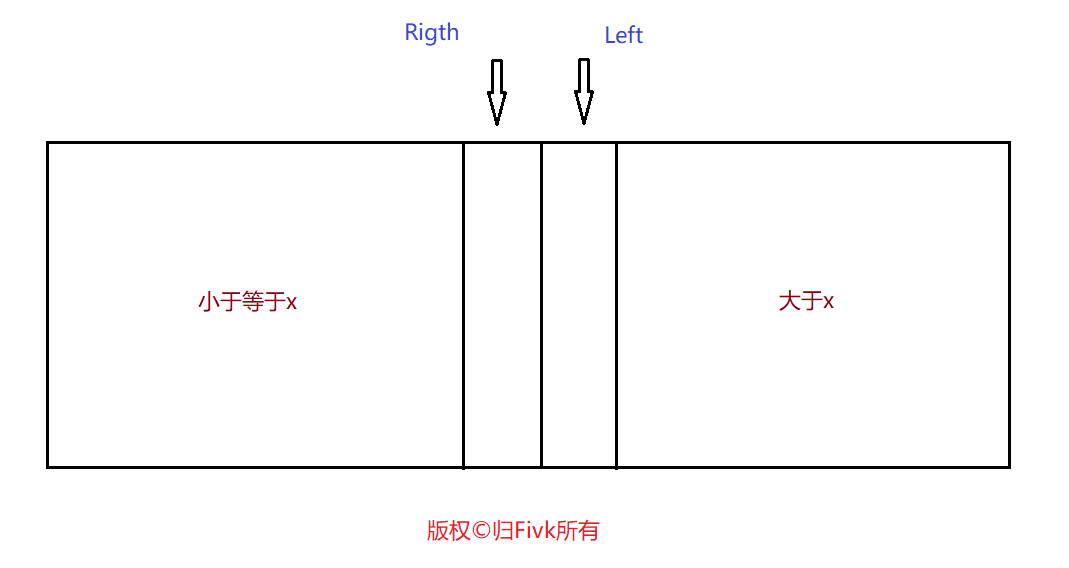

![](https://blog.fivk.cn/usr/uploads/2021/05/2071262191.png)

最终循环结束时一定是Left=Right+1，根据二分的2步的做法我们知道Right的右边一定是大于x的，而根据第3步我们可以知道Left左边一定是小于等于x的。

所以，一目了然，最终答案是Right指向的数。Right=0就是题目中输出-1的情况。

```Cpp
#include<iostream>
using namespace std;

int n, m, a[110000];
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    a[0] = -1;
    for (int i = 1; i <= m; i++)
    {
        int x;
        int left = 1, right = n, mid;
        cin >> x;
        while (left <= right)
        {
            mid = (left + right) / 2;
            if (a[mid] <= x)
            {
                left = mid + 1;
            }
            else {
                right = mid - 1;
            }
        }
        cout << a[right] << endl;
        //输出a[mid]的话就是第一个大于它的数以为mid=right+1（right=mid-1）
    }

return 0;
}
```

## 例2：快速排序(Quicksort)

快速排序有C.A.R.Hoare在1962年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

设要排序的数组是A[1]……A[N],首先任意选取一个数据（通常选用数组的中间数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

</div>

一趟快速排序的算法是：

1. 设置两个变量i、j，排序开始的时候：i=1，j=N;
2. 以数组中任意两个元素作为关键数据（一般以数组中间元素作为关键数据），赋值给key，可以是key=A[(i+j)/2];
3. 从j开始向前搜索，即由后开始向前搜索（j--），找到的一个小于等于key的值A[j];
4. 从i开始向后搜索，即由前开始向后搜索（i++），找到第一个大于等于key的A[i];
5. 交换A[i]和A[j]的值，同时i++，j--;
6. 重复的3、4、5步，直到i>j;

![](https://blog.fivk.cn/usr/uploads/2021/05/556719723.png)

此时i>j，并且i左边的数字都小于等于key，j右边的数字都大于等于key，进而接下来可以分别对左边段[i,j]和右边段[i,N]利用同样的方法排序。

```cpp
#include<iostream>
using namespace std;

void qsort(int, int);
int a[101];
int main()
{
	int n, i;
	cin >> n;
	for (i = 1; i <= n; i++)
		cin >> a[i];
	qsort(1, n);
	for (i = 1; i <= n; i++)
		cout << a[i] << " ";
	cout << endl;
	return 0;
}

void qsort(int l, int r)
{
	int i, j, mid, p;
	i = l;
	j = r;
	mid = a[(l + r) / 2];	//当前程序在中间位置的数定义为分隔数
	while (i <= j)
	{
		while (a[i] < mid) i++;	//在左半部分寻找比中间数大的数
		while (a[j] > mid) j--;	//在右半部分寻找比中间数小的数
		if (i <= j)
		{						//若找到一组与排序目标不一致的数对，则交换他们
			p = a[i];
			a[i] = a[j];
			a[j] = p;
			i++;
			j--;				//继续找
		}
	}

if (l < j) qsort(l, j);		//若未到两个数的边界，则递归搜索左右区间
	if (i < r) qsort(i, r);

}
```

快速排序(Quicksort)是对冒泡排序的一种改进，快速排序的时间复杂程度是O(nlogn)，速度快，但它是不稳定的排序方法。就平均时间而言，快速排序是目前被认为是最好的一种排内部排序方法。但快速排序需要一个栈空间来实现递归，若每一趟排序都将记录序列均匀的分割成长度相似的两个子序列，则栈的最大深度为log(n+1)。

## 例3：一元三次方程求解

如形如有$ax^{3}+bx^{2}+cx+d=0$ 一个元三次方程。给出该方程中各项的系数（a、b、c、d均为实数），并约定该方程存在三个不同实根（根的氛围在-100至100之间），且根与根之差的绝对值 $\geq$ 1。

要求由大到小依次在同一行输出这三个实根（根与根从小到大留有空格），并精确到小数点后2位。

提示：记方程$f(x)=0$ ，若存在2个数 $x_1$ 与 $x_2$ ,且 $x_1<x_2,f(x_1)*f(x_2)<0$ 则在$(x_1,x_2)$ 之间一定有一个根。

> 输入：
>
> a b c d

> 输出：
>
> 三个实根（根与根之间保留有空格）

</div>

【输入样例】

```输入样例
1 -5 -4 20
```

【输出样例】

```输出样例
-2.00 2.00 5.00
```

这是一道有趣的解方程题。为了便于求解，设方程$f(x)=ax^{3}+bx^{2}+cx+d=0$ ,设根的值域(-100至100之间)中有x，其左右两边相距0.0005的敌方有$x_1$和$x_2$ 两个数，即$x_1=x-0.0005,x_2=x+0.0005$ 。$x_1$ 和 $x_2$ 间的距离(0.001)满足进度要求(精确到小数点后两位)。若出现如图所示的两种情况之一，则确定x为$f(x)=0$ 的根。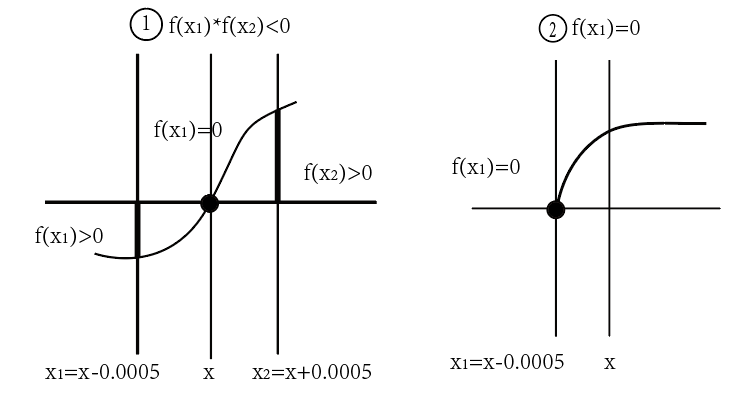

![](https://blog.fivk.cn/usr/uploads/2021/05/4100581259.png)

有两种方法计算$f(x)=0$ 的根x:

* (1)**枚举法**

根据值域和根与根之间的距离要求($\ge$ 1)，我们不妨将根的值域扩大100倍(-10000$\le$ x$\le$ 10000)，依次枚举该区域的每一个整数值x，并在题目要求的精度内设定区间:$x_1=\frac{x-0.05}{100},x_2=\frac{x+0.05}{100}$ 。若区间端点的函数值$f(x_1)$ 和$f(x_2)$ 异号或者在区间端点$x_1$ 的函数值$f(x_1)=0$ 则确定$\frac{x}{100}$ 为$f(x)=0$ 的一个根。

**由此得出算法：**

```cpp
//输入方程中各项系数 a b c d
for (x = -10000; x <= 10000; x++)		//枚举当前根*100的可能范围
{
	x1 = (x - 0.05) / 100;				//在要求的精度内设定区间
	x2 = (x + 0.05) / 100;
	if ((f(x1) * f(x2) < 0) || f(x1) == 0)
	{						//若在区间两端的函数异号或在x1处的函数值为0
		printf("%.2lf", x / 100);		//则确定x/100为根
	}
}

//函数f(x)
double f(double x)
{
	return a * x * x * x + b * x * x + c * x + d;
}
```

- (2)分治法

枚举根的值域中的每一个整数x(-100$\le$x$\le$ 100)。由于根与根之差的绝对值$\ge$ 1，因此设定搜索区间$[x_1,x_2]$ ，其中$x_1=x,x_2=x+1$ 。

1. $f(x_1)=0$ 则确定$x_1$ 为$f(x)$ 的根;
2. 若$f(x_1)*f(x_2)>0$ 则确定根x不在区间$[x_1,x_2]$ 内，设定$[x_2,x_2+1]$ 为下一个搜索区间;
3. 若$f(x_1)*f(x_2)<0$ 则确定根在区间$[x_1,x_2]$ 内。

如果确定根x在区间$[x_1,x_2]$ 内的话（$f(x_1)*f(x_2)<0$ ），如何在该区间找到根的确切位置。采用二分法，将区间$[x_1,x_2]$ 分成左右两个子区间:左子区间$[x_1,x]$ 和右子区间$[x,x_2]$ （其中$x=\frac{x_1+x_2}{2}$）：

> 若$f(x_1)*f(x_2)<=0$ ，则确定根在左子区间，将x设为该区间的右指针($x_2=x$)，继续对左子区间进行对分析;若$f(x_1)*f(x_2)>0$，则确定根在右区间$[x,x_2]$内，将x设为该区间1的左指针($x_1=x$)，继续对右子区间进行对分;

上述对分过程一直进行到区间距离满足精度要求为止($x_2-x_1<0.001$)。此时确定$x_1$为$f(x)$的根。

由此得出算法:

```cpp
	输入方案中各项的系数a、b、c、d;
	for (x = -100; x <= 100; x++)	//枚举每一种可能的根
	{
		x1 = x;
		x2 = x + 1;					//确定根的可能区间
		if (f(x1) == 0)				//若x1为根，则输出
		{
			printf("%.2lf ", x1);
		}
		else if (f(x1) * f(x2) < 0)	//若根在[x1,x2]中
		{
			while (x2 - x1 >= 0.001)	//若区间[x1,x2]不满足精度要求，则循环
			{
				xx = (x1 + x2) / 2;	//计算区间[x1,x2]的中间位置
				if (f(x1) * f(xx) <= 0)	//若根在左子区间，则调整右指针
				{
					x2 = xx;
				}
				else {
					x1 = xx;			//若根在右子区间，则调整左指针
				}
			}
			printf("%.2lf ", x1);		//区间[x1,x2]满足精度要求，确定x1为根
		}
	}
}

double f(double x)		//计算函数值
{
	return a * x * x * x + b * x * x + c * x + d;
}
```

* 枚举

```cpp
#include<iostream>
using namespace std;

double f(double x);

double x, a, b, c, d, x1, x2;

int main()
{
	cin>>a>>b>>c>>d; 
	//输入方程中各项系数 a b c d
	for (x = -10000; x <= 10000; x++)		//枚举当前根*100的可能范围
	{
		x1 = (x - 0.05) / 100;				//在要求的精度内设定区间
		x2 = (x + 0.05) / 100;
		if ((f(x1) * f(x2) < 0) || f(x1) == 0)
		{									//若在区间两端的函数异号或在x1处的函数值为0
			printf("%.2lf \n", (double)(x / 100.0));		//则确定x/100为根
		}
	}
	return 0;
}

//函数f(x)
double f(double x)
{
	return a * x * x * x + b * x * x + c * x + d;
}
```

* 分治

```cpp
#include<iostream>
using namespace std;
double f(double x);

double a, b, c, d;
double x1, x2, x, xx;

int main()
{
	cin >> a >> b >> c >> d;
	for (x = -100; x <= 100; x++)	//枚举每一种可能的根
	{
		x1 = x;
		x2 = x + 1;					//确定根的可能区间
		if (f(x1) == 0)				//若x1为根，则输出
		{
			printf("%.2lf ", x1);
		}
		else if (f(x1) * f(x2) < 0)	//若根在[x1,x2]中
		{
			while (x2 - x1 >= 0.001)	//若区间[x1,x2]不满足精度要求，则循环
			{
				xx = (x1 + x2) / 2;	//计算区间[x1,x2]的中间位置
				if (f(x1) * f(xx) <= 0)	//若根在左子区间，则调整右指针
				{
					x2 = xx;
				}
				else {
					x1 = xx;			//若根在右子区间，则调整左指针
				}
			}
			printf("%.2lf ", x1);		//区间[x1,x2]满足精度要求，确定x1为根
		}
	}
}

double f(double x)		//计算函数值
{
	return a * x * x * x + b * x * x + c * x + d;
}
```

昨天在PTA做ACM训练时刚好有一道类似的题：

> 7-2 二分法求多项式单根 (20 分)
>
> 二分法求函数根的原理为：如果连续函数f(x)在区间[a,b]的两个端点取值异号，即f(a)f(b)<0，则它在这个区间内至少存在1个根r，即f(r)=0。
>
> 二分法的步骤为：
>
> * 检查区间长度，如果小于给定阈值，则停止，输出区间中点(a+b)/2；否则
> * 如果f(a)f(b)<0，则计算中点的值f((a+b)/2)；
> * 如果f((a+b)/2)正好为0，则(a+b)/2就是要求的根；否则
> * 如果f((a+b)/2)与f(a)同号，则说明根在区间[(a+b)/2,b]，令a=(a+b)/2，重复循环；
> * 如果f((a+b)/2)与f(b)同号，则说明根在区间[a,(a+b)/2]，令b=(a+b)/2，重复循环。
>
> 本题目要求编写程序，计算给定3阶多项式f(x)=a3x3+a2x2+a1x+a0在给定区间[a,b]内的根。
>
> **输入格式：**
>
> 输入在第1行中顺序给出多项式的4个系数a3、a2、a1、a0，在第2行中顺序给出区间端点a和b。题目保证多项式在给定区间内存在唯一单根。
>
> **输出格式：**
>
> 在一行中输出该多项式在该区间内的根，精确到小数点后2位。
>
> **输入样例：**
>
> ```in
> 3 -1 -3 1
> -0.5 0.5
> ```
>
> 输出样例：
>
> ```out
> 0.33
> ```

我写的：

```cpp
#include<bits/stdc++.h>

using namespace std;

double a1,a2,a3,a0;
double a,b;

double f(double x)
{
	return a3*x*x*x+a2*x*x+a1*x+a0;
}

int main()
{
	double n,i,x1,x2,F;
	cin>>a3>>a2>>a1>>a0;
	cin>>a>>b;

while(1)
	{
		if(b-a<0.00999)
	{
		printf("%.2lf",(a+b)/2);
		return 0;
	}
		if(f((a+b)/2)==0)
		{
			F = (a+b)/2;
			break;
		}else if(f((a+b)/2)*f(a)>0)
		{
			a=(a+b)/2;
		}else if(f((a+b)/2)*f(b)>0){
			b=(a+b)/2;
		}
	}

printf("%.2lf",F);
	return 0;
}

```

## 例4：循环比赛日程(match)

设有n个选手进行循环比赛，其中$n=2^m$ 要求每名选手要与其他n-1名选手都赛一次，每名选手每天比赛一次，循环赛共进行n-1天，要求每天没有选手轮空。

> 输入:m
>
> 输出:表格形式的比赛安排表

</div>

【输入样例】

```cin
3
```

【输出样例】

```cout
   1   2   3   4   5   6   7   8
   2   1   4   3   6   5   8   7
   3   4   1   2   7   8   5   6
   4   3   2   1   8   7   6   5
   5   6   7   8   1   2   3   4
   6   5   8   7   2   1   4   3
   7   8   5   6   3   4   1   2
   8   7   6   5   4   3   2   1
```

以$m=3$(即$n=2^{3}$)为例，可以根据问题要求，制定出如下表所示的一种方案: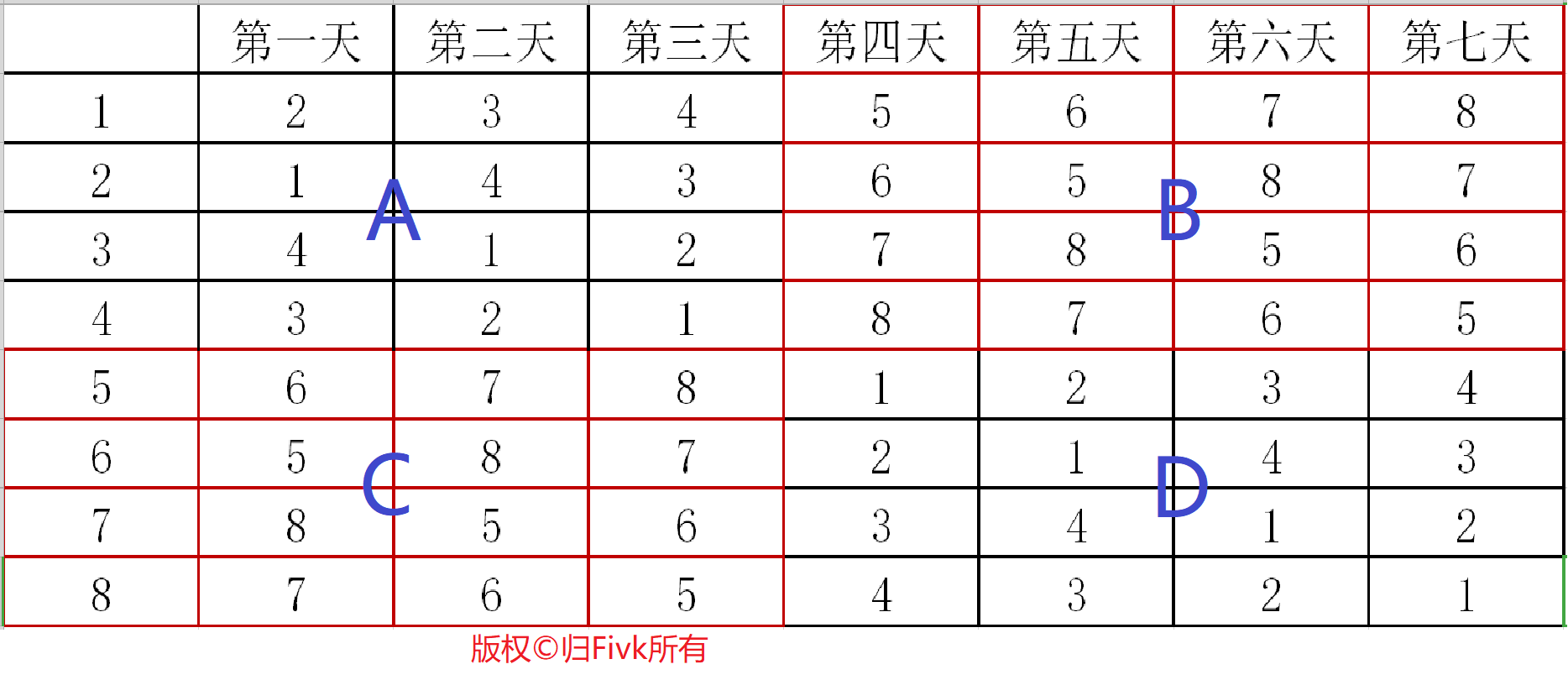

![](https://blog.fivk.cn/usr/uploads/2021/05/3015861027.png)

以表格的中心为拆分点，将表格分成A、B、C、D四个部分，就很容易看出有A=D,B=C,并且这一规律同样适用于各个更小的部分。

设有n个选手的循环比赛，其中$n=2^{m}$。要求每名选手要与其他n-1名选手都赛一次。每名选手每天比赛一次，循环赛共进行n-1天。要求每天没有选手轮空，一下是八名选手时的循环比赛表，表中第一行为八名选手的编号，下面依次是每名选手每天的对手。

1 2 3 4 5 6 7 8

2 1 4 3 6 5 8 7

3 4 1 2 7 8 5 6

4 3 2 1 8 7 6 5

5 6 7 8 1 2 3 4

6 5 8 7 2 1 4 3

7 8 5 6 3 4 1 2

8 7 6 5 4 3 2 1

从八位选手的循环比赛表中可以看出，这是一个具有对称性的方阵，可以把方阵一分为四来看，那么左上角的$4*4$的方阵就是前四位选手的循环比赛表，而右上角的$4*4$的方阵就是后四位选手的循环比赛表，它们在本质上是一样的，都是4个选手的循环比赛表，所不同的只是选手编号不同而已，**将左上角方阵所有元素加上4就能得到右上角的方阵。** 下方的两个方阵表示前四位选手和后四位选手进行交叉循环比赛的情况，同样具有对称性，将右上角方阵复制到左下角即得到1、2、3、4四位选手和5、6、7、8四位选手的循环比赛表，根据对称性，右下角的方阵应与右上角的方阵相同。这样，八名选手的循环比赛可以由四名选手的循环比赛表根据对称性生成出来。同样的，两名选手的循环比赛表可以说是已知的，这种程序设计方法叫做分治法，其基本思想是把一个规模为n的问题分成若干个规模较小的问题，使得从这些较小问题的解易于构造出整个问题的解。

程序中用数组matchlist记录n名选手的循环比赛表，整个循环比赛从最初$1*1$的方阵按上述规则生成出$2*2$的方阵，再生产出$4*4$的方阵，……，直到生成出整个循环比赛表为止。变量half表示当前方阵的大小，也是要生成下一个方阵的大小的一半。

```cpp
#include<cstdio>

const int MAXN = 1025, MAXM = 11;
int matchlist[MAXN][MAXM];
int m;

int main()
{
	printf("Input m:");
	scanf("%d", &m);
	int n = 1 << m, k = 1, half = 1; //1<<m相当于2^m
	matchlist[0][0] = 1;
	while (k <= m)			//构造m次就将2^m个人排好了
	{
		for (int i = 0; i < half; i++)
		{
			for (int j = 0; j < half; j++)
			{
				matchlist[i][j + half] = matchlist[i][j] + half;
				//构造右上方方阵
			}
		}

for (int i = 0; i < half; i++)
		{
			for (int j = 0; j < half; j++)
			{
				matchlist[i + half][j] = matchlist[i][j + half];
					//左下角方正等于右上角方阵

matchlist[i + half][j + half] = matchlist[i][j];
					//右下角方阵等于左上角方阵
			}
		}
		half *= 2;
		k++;
	}

for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
			printf("%4d", matchlist[i][j]);
		printf("\n");
	}

return 0;
}
```

我写的：

```cpp
#include<stdio.h>
int a[1025][1025];

int main()
{
	int m,l=1,n;

scanf("%d",&m);
	n=1<<m;
	a[0][0]=1;	//第一个位置是1

while(m--)
	{
		for(int i=0;i<l;i++)
		{
			for(int j=0;j<l;j++)
			{
				//右上角 
				a[i][j+l]=a[i][j]+l;

//右下角
				a[i+l][j+l]=a[i][j];

//左下角 
				a[i+l][j]=a[i][j+l];

//右上角是已知的不需要复制 
			}
		}
		l*=2;
	}

for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			printf("%d ",a[i][j]);
		}
		printf("\n");
	}

return 0;
}
```

## 例5：取模运算（mod）

输入b、p、k的值，求$b^p mod k$的值。其中b、p、k为长整型数。

</div>

【输入样例】

```cin
2 10 9
```

【输出样例】

```cout
2^10 mod 9 = 7
```

本题主要的难点在于数据规模很大(b、p都是长整型)，对于$p^{b}显然不能死算，那样的话时间复杂度和编程复杂度都很大。

下面介绍一个原理:a * b%k=(a%k) * (b%k)%k。显然有了这个原理，就可以把较大的幂分解成较小的，因而免去高精度计算等复杂过程。那么怎样分解最有效呢？显然对于任何一个自然数p，有p = 2 * p/2 + p%2，如19 = 2 * 19 + 19%2 = 2 * 9 + 1，利用上述原理就可以把b的19次方转换成为求b的9次方除以k的余数，即$b^{19}=b^{2*9+1}=b*b^{9}*b^{9}$，再进一步分解下去就不难求得整个问题的解。

```cpp
#include<iostream>
#include<cstdio>
using namespace std;

int b, p, k, a;

int f(int p)					//利用分治求b^p%k
{
	if (p == 0) return 1;		//b^0=1

int tmp = f(p / 2) % k;
	tmp = (tmp * tmp) % k;		//b^p%k=(b^(p/2))^2^k

if (p % 2 == 1)
		tmp = (tmp * (b % k)) % k;
								//如果p为基数，则b^p%k=((b^(p/2))^2)*b%k
	return tmp;
}

int main()
{
	cin >> b >> p >> k;
	int tmpb = b;
	b %= k;
	printf("%d^%d mod %d = %d\n", tmpb, p, k, f(p));
	return 0;
}

```

我改写的，可能这样要看的懂一点点。

```cpp
#include<stdio.h>
int b, p, k;

int f(int p)
{
	if (p == 0) return 1;
	int tmp = f(p / 2);		//防止条用次数过多，先保存数值 
	if (p % 2 == 0)
	{
		tmp = (tmp % k * tmp % k) % k;
	}
	else {
		tmp = (b % k * tmp % k * tmp % k) % k;
	}
	return tmp;
}

int main()
{
	scanf("%d %d %d", &b, &p, &k);
	int pb = b;
	printf("%d^%d mod %d = %d", pb, p, k, f(p));
	return 0;
}
```

其实这个算法20年10月我就已经发在博客上了，哈哈哈，速度来说感觉这个要快一点。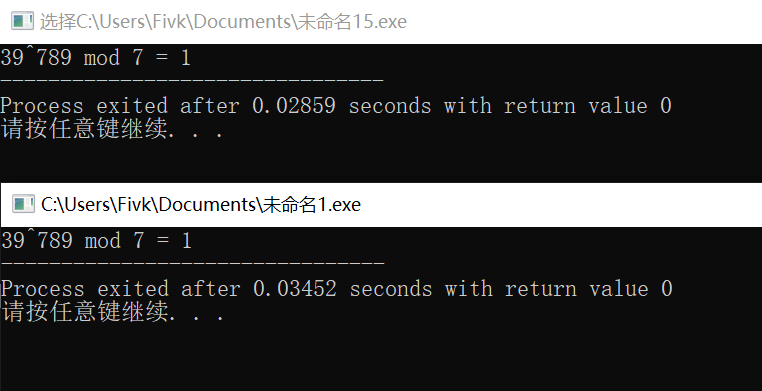

![](https://blog.fivk.cn/usr/uploads/2021/05/1459179409.png)

分治0.03452，我的是0.02859。快一点没错啦。

实现代码：

```c
#include<stdio.h>
int main()
{
	int a,b,c;
	scanf("%d %d %d",&a,&b,&c);
	int x=1;
	for(int i=1;i<=b;i++)
	{
		x*=a;
		x=x%c;
	}
	printf("%d^%d mod %d = %d",a,b,c,x);
	return 0;
}
```

算法原理：

<div class="inner-content" >
<p class="inser-title">【C】指数取余</p>
<div class="inster-summary text-muted">
先来看两道题这里就不能直接算了没有任何数据可以储存所以我们需要定义一个算法发现一篇文章还挺好的对于上面的题有这些算...
</div>
</div>
</a>

</div>

</div>

## 例6：黑白棋子的移动（chessman）

有2n个棋子($n\geq4$)排成一行，开始位置为白子全部再左边，黑子全部再右边，下面图为n=5的情况：

![](https://blog.fivk.cn/usr/uploads/2021/05/1313327302.png)

移动棋子的规则是：每次必须同时移动相邻的两个棋子，颜色不限，可以左移也可以右移到空位去，但不能调换两个棋子的左右位置。每次移动必须跳过若干个棋子（不能平移），要求最后能移成黑白相间的一行棋子。如n=5时，成为：

![](https://blog.fivk.cn/usr/uploads/2021/05/917883748.png)

</div>

【输入样例】

```cin
7
```

【输出样例】

```cout
step0:ooooooo*******--
step1:oooooo--******o*
step2:oooooo******--o*
step3:ooooo--*****o*o*
step4:ooooo*****--o*o*
step5:oooo--****o*o*o*
step6:oooo****--o*o*o*
step7:ooo--***o*o*o*o*
step8:ooo*o**--*o*o*o*
step9:o--*o**oo*o*o*o*
step10:o*o*o*--o*o*o*o*
step11:--o*o*o*o*o*o*o*
```

我们先从n=4开始试试看，初始时：

○○○○●●●●

* 第一步：○○○——●●●○●  //—表示空位
* 第二步：○○○●○●●——●
* 第三步：○——●○●●○○●
* 第四步：○●○●○●——○●
* 第五步：——○●○●○●○●

如果n=5呢？我们继续尝试，希望看出一些规律，初始时：

○○○○○●●●●●

* 第一步：○○○○—●●●●○●
* 第二步：○○○○●●●●—○●

这样n=5的问题又分解成了n=4的情况，下面只要再做一次n=4的5个步骤就行了。同理n=6的情况又可分解成n=5的情况，……，所以，对于一个规模为n的问题，我们很容易地就把他分治成了规模为n-1的相同类型的子问题。

数据结构如下：数组c[1...max]用来作为棋子移动的场所，初始时，c[1] ~ c[n]存放白字(用字符o表示)，c[n+1] ~ c[2n]存放黑子(用字符*表示)，c[2n+1]，c[2n+2]为空位置(用字符—表示)。最后结果在c[3]~c[2n+2]中。

```cpp
#include<iostream>
using namespace std;

int n, st, sp;
char c[101];

void print()		//打印
{
	int i;
	cout << "step" << st << ':';
	for (i = 1; i <= 2 * n + 2; i++) cout << c[i];
	cout << endl;
	st++;
}

void init(int n)	//初始化
{
	int i;
	st = 0;
	sp = 2 * n + 1;
	for (i = 1; i <= n; i++) c[i] = 'o';
	for (i = n + 1; i <= 2 * n; i++) c[i] = '*';
	c[2 * n + 1] = '-';
	c[2 * n + 2] = '-';
	print();
}

void move(int k)	//移动一步
{
	int j;
	for (j = 0; j <= 1; j++)
	{
		c[sp + j] = c[k + j];
		c[k + j] = '-';
	}
	sp = k;
	print();
}

void mv(int n)		//主要过程
{
	int i, k;
	if (n == 4)		//n等于4的情况要特殊处理
	{
		move(4);
		move(8);
		move(2);
		move(7);
		move(1);
	}
	else {
		move(n);
		move(2 * n - 1);
		mv(n - 1);
	}
}

int main()
{
	cin >> n;
	init(n);
	mv(n);
}
```

## 例7：光荣的梦想

Prince对他在这片大陆上维护的秩序感到满意，于是决定启程离开艾泽拉斯。在他动身之前，Prince决定赋予King_Bette最强大的能量以守护世界、保卫这里的平衡与和谐。在那个时代，平衡是个梦想。因为有很多奇异的物种拥有各种不稳定的能量，平衡瞬间即被打破。KB决定求助你，帮助他完成这个梦想。

一串数列即表示一个世界状态。

平衡是指这串数列以升序排列。而从一串无序数列到有序数列需要通过交换数列中的元素来实现。KB的能量只能交换相邻两个数字。他想知道最少需要交换几次就能使数列有序。

【输入格式】

第一行为数列中的个数n，

第2行为n<=10000个数。表示当前数列状态。

【输出格式】

输出一个整数，表示最少需要交换几次能达到平衡状态。

</div>

```in
4
2 1 4 3
```

```out
2
```

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-b6ab7f9b1603fa4596e00ffd7ed5037535" aria-expanded="true"><div class="accordion-toggle"><span style="">【算法分析】：归并排序求逆序对</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-b6ab7f9b1603fa4596e00ffd7ed5037535" class="collapse collapse-content"><p></p>

归并排序：假设我们已经将区间[L,K]和区间[K+1,R]排好序，则我们可以花费线性的复杂度将区间[L,R]排好序。

最后修改：2021 年 09 月 12 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

【算法基础】分治算法

Fivk • 2021 年 05 月 08 日

需要注意的是使用二分法有一个重要的前提，就是有序性，下面通过几个例子来体会二分法的应用。

# 经典案例

## 例1：找数

描述：

给一个长度为n的单调递增的正整数序列，即序列中每一个数都比前一个数大。有m个询问，每次询问一个x，问序列中最后一个小于等于x的数是什么？

**输入：**

第一行两个整数n,m。

接下来一行n个数，表示这个序列。

接下来m行每行一个数，表示一个询问。

**输出：**

输出共m行，表示序列中最后一个小于等于x的数是什么。假设没有，则输出-1。

</div>

【输入样例】

```输入样例
5 3
1 2 3 4 6
5
1 
3
```

【输出样例】

```输出样例
4
1
3
```

**每一次二分，我们这样来做：**

**重复执行二分法操作直到Left>Right。**

下面我们来分析答案的情况。<span style="color:#A52A2A">循环结束</span>示意图：

![](https://blog.fivk.cn/usr/uploads/2021/05/2071262191.png)

最终循环结束时一定是Left=Right+1，根据二分的2步的做法我们知道Right的右边一定是大于x的，而根据第3步我们可以知道Left左边一定是小于等于x的。

所以，一目了然，最终答案是Right指向的数。Right=0就是题目中输出-1的情况。

```Cpp
#include<iostream>
using namespace std;

return 0;
}
```

## 例2：快速排序(Quicksort)

</div>

一趟快速排序的算法是：

![](https://blog.fivk.cn/usr/uploads/2021/05/556719723.png)

此时i>j，并且i左边的数字都小于等于key，j右边的数字都大于等于key，进而接下来可以分别对左边段[i,j]和右边段[i,N]利用同样的方法排序。

```cpp
#include<iostream>
using namespace std;

if (l < j) qsort(l, j);		//若未到两个数的边界，则递归搜索左右区间
	if (i < r) qsort(i, r);

}
```

## 例3：一元三次方程求解

要求由大到小依次在同一行输出这三个实根（根与根从小到大留有空格），并精确到小数点后2位。

提示：记方程$f(x)=0$ ，若存在2个数 $x_1$ 与 $x_2$ ,且 $x_1<x_2,f(x_1)*f(x_2)<0$ 则在$(x_1,x_2)$ 之间一定有一个根。

> 输入：
>
> a b c d

> 输出：
>
> 三个实根（根与根之间保留有空格）

</div>

【输入样例】

```输入样例
1 -5 -4 20
```

【输出样例】

```输出样例
-2.00 2.00 5.00
```

![](https://blog.fivk.cn/usr/uploads/2021/05/4100581259.png)

有两种方法计算$f(x)=0$ 的根x:

* (1)**枚举法**

**由此得出算法：**

//函数f(x)
double f(double x)
{
	return a * x * x * x + b * x * x + c * x + d;
}
```

- (2)分治法

枚举根的值域中的每一个整数x(-100$\le$x$\le$ 100)。由于根与根之差的绝对值$\ge$ 1，因此设定搜索区间$[x_1,x_2]$ ，其中$x_1=x,x_2=x+1$ 。

上述对分过程一直进行到区间距离满足精度要求为止($x_2-x_1<0.001$)。此时确定$x_1$为$f(x)$的根。

由此得出算法:

double f(double x)		//计算函数值
{
	return a * x * x * x + b * x * x + c * x + d;
}
```

* 枚举

```cpp
#include<iostream>
using namespace std;

double f(double x);

double x, a, b, c, d, x1, x2;

//函数f(x)
double f(double x)
{
	return a * x * x * x + b * x * x + c * x + d;
}
```

* 分治

```cpp
#include<iostream>
using namespace std;
double f(double x);

double a, b, c, d;
double x1, x2, x, xx;

double f(double x)		//计算函数值
{
	return a * x * x * x + b * x * x + c * x + d;
}
```

昨天在PTA做ACM训练时刚好有一道类似的题：

我写的：

```cpp
#include<bits/stdc++.h>

using namespace std;

double a1,a2,a3,a0;
double a,b;

double f(double x)
{
	return a3*x*x*x+a2*x*x+a1*x+a0;
}

int main()
{
	double n,i,x1,x2,F;
	cin>>a3>>a2>>a1>>a0;
	cin>>a>>b;

printf("%.2lf",F);
	return 0;
}

```

## 例4：循环比赛日程(match)

> 输入:m
>
> 输出:表格形式的比赛安排表

</div>

【输入样例】

```cin
3
```

【输出样例】

以$m=3$(即$n=2^{3}$)为例，可以根据问题要求，制定出如下表所示的一种方案:

![](https://blog.fivk.cn/usr/uploads/2021/05/3015861027.png)

以表格的中心为拆分点，将表格分成A、B、C、D四个部分，就很容易看出有A=D,B=C,并且这一规律同样适用于各个更小的部分。

1 2 3 4 5 6 7 8

2 1 4 3 6 5 8 7

3 4 1 2 7 8 5 6

4 3 2 1 8 7 6 5

5 6 7 8 1 2 3 4

6 5 8 7 2 1 4 3

7 8 5 6 3 4 1 2

8 7 6 5 4 3 2 1

```cpp
#include<cstdio>

const int MAXN = 1025, MAXM = 11;
int matchlist[MAXN][MAXM];
int m;

for (int i = 0; i < half; i++)
		{
			for (int j = 0; j < half; j++)
			{
				matchlist[i + half][j] = matchlist[i][j + half];
					//左下角方正等于右上角方阵

matchlist[i + half][j + half] = matchlist[i][j];
					//右下角方阵等于左上角方阵
			}
		}
		half *= 2;
		k++;
	}

for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
			printf("%4d", matchlist[i][j]);
		printf("\n");
	}

return 0;
}
```

我写的：

```cpp
#include<stdio.h>
int a[1025][1025];

int main()
{
	int m,l=1,n;

scanf("%d",&m);
	n=1<<m;
	a[0][0]=1;	//第一个位置是1

while(m--)
	{
		for(int i=0;i<l;i++)
		{
			for(int j=0;j<l;j++)
			{
				//右上角 
				a[i][j+l]=a[i][j]+l;

//右下角
				a[i+l][j+l]=a[i][j];

//左下角 
				a[i+l][j]=a[i][j+l];

//右上角是已知的不需要复制 
			}
		}
		l*=2;
	}

for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			printf("%d ",a[i][j]);
		}
		printf("\n");
	}

return 0;
}
```

## 例5：取模运算（mod）

输入b、p、k的值，求$b^p mod k$的值。其中b、p、k为长整型数。

</div>

【输入样例】

```cin
2 10 9
```

【输出样例】

```cout
2^10 mod 9 = 7
```

本题主要的难点在于数据规模很大(b、p都是长整型)，对于$p^{b}显然不能死算，那样的话时间复杂度和编程复杂度都很大。

```cpp
#include<iostream>
#include<cstdio>
using namespace std;

int b, p, k, a;

int f(int p)					//利用分治求b^p%k
{
	if (p == 0) return 1;		//b^0=1

int tmp = f(p / 2) % k;
	tmp = (tmp * tmp) % k;		//b^p%k=(b^(p/2))^2^k

if (p % 2 == 1)
		tmp = (tmp * (b % k)) % k;
								//如果p为基数，则b^p%k=((b^(p/2))^2)*b%k
	return tmp;
}

int main()
{
	cin >> b >> p >> k;
	int tmpb = b;
	b %= k;
	printf("%d^%d mod %d = %d\n", tmpb, p, k, f(p));
	return 0;
}

```

我改写的，可能这样要看的懂一点点。

```cpp
#include<stdio.h>
int b, p, k;

int main()
{
	scanf("%d %d %d", &b, &p, &k);
	int pb = b;
	printf("%d^%d mod %d = %d", pb, p, k, f(p));
	return 0;
}
```

其实这个算法20年10月我就已经发在博客上了，哈哈哈，速度来说感觉这个要快一点。

![](https://blog.fivk.cn/usr/uploads/2021/05/1459179409.png)

分治0.03452，我的是0.02859。快一点没错啦。

实现代码：

```c
#include<stdio.h>
int main()
{
	int a,b,c;
	scanf("%d %d %d",&a,&b,&c);
	int x=1;
	for(int i=1;i<=b;i++)
	{
		x*=a;
		x=x%c;
	}
	printf("%d^%d mod %d = %d",a,b,c,x);
	return 0;
}
```

算法原理：

## 例6：黑白棋子的移动（chessman）

有2n个棋子($n\geq4$)排成一行，开始位置为白子全部再左边，黑子全部再右边，下面图为n=5的情况：

![](https://blog.fivk.cn/usr/uploads/2021/05/1313327302.png)

![](https://blog.fivk.cn/usr/uploads/2021/05/917883748.png)

</div>

【输入样例】

```cin
7
```

【输出样例】

我们先从n=4开始试试看，初始时：

○○○○●●●●

如果n=5呢？我们继续尝试，希望看出一些规律，初始时：

○○○○○●●●●●

* 第一步：○○○○—●●●●○●
* 第二步：○○○○●●●●—○●

```cpp
#include<iostream>
using namespace std;

int n, st, sp;
char c[101];

void print()		//打印
{
	int i;
	cout << "step" << st << ':';
	for (i = 1; i <= 2 * n + 2; i++) cout << c[i];
	cout << endl;
	st++;
}

void move(int k)	//移动一步
{
	int j;
	for (j = 0; j <= 1; j++)
	{
		c[sp + j] = c[k + j];
		c[k + j] = '-';
	}
	sp = k;
	print();
}

int main()
{
	cin >> n;
	init(n);
	mv(n);
}
```

## 例7：光荣的梦想

一串数列即表示一个世界状态。

【输入格式】

第一行为数列中的个数n，

第2行为n<=10000个数。表示当前数列状态。

【输出格式】

输出一个整数，表示最少需要交换几次能达到平衡状态。

</div>

```in
4
2 1 4 3
```

```out
2
```

归并排序：假设我们已经将区间[L,K]和区间[K+1,R]排好序，则我们可以花费线性的复杂度将区间[L,R]排好序。

【算法基础】分治算法

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【开发技巧】@CrossOrigin注解解决跨域问题

【C】极域电子教室学生端解除控制

这是好东西

【Fivk】文章归档

【Linux】shell 文本三剑客之正则表达式

Conda常用命令整理

【前端笔记】Vue3

【C】指针运算

【c】国王将金币作为工资，发放给忠诚的骑士

【算法基础】分治算法

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

【算法基础】分治算法

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款