Loading... # 算法介绍 搜索与回溯是计算机解题中常用的算法,很多问题无法根据某种确定的计算法则来求解,可以利用搜索与回溯的技术求解。回溯是搜索算法中的一种控制策略。它的基本思想是:为了求得问题的解,先选择某一种可能情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直到得到解或证明无解。 如迷宫问题:进入迷宫,先随意选择一个前进方向,一步步向前试探前进,如果碰到死胡同,说明前进方向已经无路可走。这时首先看其他地方是否还有其他路可走:如果有路可走,则沿该方向再向前试探;如果已无路可走,则返回一步,再看其他方向是否还有路可走。按此原则不断搜索回溯再搜索,直到找到新的出入或从原路返回入口处无解为止。 --- # 算法框架 * 递归回溯算法框架[一] ```C int search(int k) { for (i = 1; j <= 算符种数; i++) { if (满足条件) { 保存结果 if (到目的地) 输出解; else search(k + 1); 恢复:保存结果之前的状态(回溯一步) } } } ``` * 递归回溯算法框架[二] ```C int search(int k) { if (目的地) 输出解; else { for(i=1;j<=算符种数;i++) if (满足条件) { 保存结果; search(k + 1); 恢复:保存结果之前的状态(回溯一步) } } } ``` --- # 算法例题 ### 例1:素数环 <div class="tip inlineBlock info"> 素数环:将1到20这20个数摆成一个环,要求相邻的两个数的和是一个素数。 </div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-0eeba8f32cb9819b1252c2b0cfb007a427" aria-expanded="true"><div class="accordion-toggle"><span style="">【算法分析】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-0eeba8f32cb9819b1252c2b0cfb007a427" class="collapse collapse-content"><p></p> 非常明显,这是一道回溯的题目。将1开始,每个空位有20种可能,只要填进去的数合法:与前面的数不相同;与左边相邻的数的和是一个素数。第20个数还要判断和第1个数的和是否素数。 <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-893cb6aa50cb7a6b2bd6441d84b337c490" aria-expanded="true"><div class="accordion-toggle"><span style="">【算法流程】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-893cb6aa50cb7a6b2bd6441d84b337c490" class="collapse collapse-content"><p></p> * 数据初始化 * 递归填数:判断第i个数填入是否合法。 1. 如果合法:填数;判断是否达到目标(20个已填完):是,打印结果;不是,递归填下一个; 2. 如果不合法:选择下一种可能。 <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-e49ce6fd240f5251ed9ea35ecaf5099221" aria-expanded="true"><div class="accordion-toggle"><span style="">【参考程序】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-e49ce6fd240f5251ed9ea35ecaf5099221" class="collapse collapse-content"><p></p> ```C++ #include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> using namespace std; bool b[21] = { 0 }; int total = 0, a[21] = { 0 }; int search(int); //回溯过程 void print(); //输出方案 bool pd(int, int); //判断素数 int main(int argc, char* argv[]) { search(1); cout << total << endl; //输出总方案数 return 0; } int search(int t) { int i; for (i = 1; i <= 20; i++) //有20个数可选 if (pd(a[t - 1], i) && (!b[i])) //判断与前一个数是否构成素数及该数是否可用 { a[t] = i; b[i] = 1; if (t == 20) { if (pd(a[20], a[1])) print(); } else { search(t + 1); } b[i] = 0; } } void print() { total++; cout << "<" << total << ">"; for (int j = 1; j <= 20; j++) cout << a[j] << " "; cout << endl; } bool pd(int x, int y) { int k = 2, i = x + y; while (k <= sqrt(i) && i % k != 0) k++; if (k > sqrt(i)) return 1; else return 0; } ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-e728bbb17f594301fdd6e6698c92f9bc44" aria-expanded="true"><div class="accordion-toggle"><span style="">【输出结果】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-e728bbb17f594301fdd6e6698c92f9bc44" class="collapse collapse-content"><p></p> 我输出了很久3天了。。。。到了6千万,然后。。不小心让电脑关机了 有兴趣的朋友可以试一试,发给博主哦^_^  <p></p></div></div></div> ### 例2:全排列 <div class="tip inlineBlock info"> 全排列plus:设有n个整数的集合{1,2,......,n},从中任意取出r个数进行排列(r<n),试列出所有的排列。 </div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-ba04c6b2e2d6d96d7fe864c14ef57a2722" aria-expanded="true"><div class="accordion-toggle"><span style="">【参考程序】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-ba04c6b2e2d6d96d7fe864c14ef57a2722" class="collapse collapse-content"><p></p> ```C++ #include<cstdio> #include<iostream> #include<iomanip> using namespace std; int num, a[10001] = { 0 }, n, r; bool b[10001] = { 0 }; void search(int); //回溯过程 void print(); //输出方案 int main() { cout << "input n,r:"; cin >> n >> r; search(1); cout << "number=" << num << endl; //输出方案总数 return 0; } void search(int k) { int i; for (i = 1; i <= n; i++) { if (!b[i]) //判断i是否可用 { a[k] = i; //保存结果 b[i] = 1; if (k == r) print(); else search(k + 1); b[i] = 0; } } } void print() { num++; for (int i = 1; i <= r; i++) cout << setw(3) << a[i]; cout << endl; } ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-0a3afe88d40adcb094ae0a54a5e011bc46" aria-expanded="true"><div class="accordion-toggle"><span style="">【输出结果】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-0a3afe88d40adcb094ae0a54a5e011bc46" class="collapse collapse-content"><p></p> 博主大一上,遇到了这个题,当真的不知道怎么下手,现在看来,是真的好简单。  <p></p></div></div></div> ### 例3:拆分自然数 <div class="tip inlineBlock info"> 任何一个大于1的自然数n,总可以拆分成若干个小于n的自然数之和。当n=7,共有14种拆分法: 7=1+1+1+1+1+1+1 7=1+1+1+1+1+2 7=1+1+1+1+3 7=1+1+1+2+2 7=1+1+2+3 7=1+1+5 7=1+2+2+2 7=1+2+4 7=1+3+3 7=1+6 7=2+2+3 7=2+5 7=3+4 total=14 </div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-3239426635481c3dfc1ef90950939a4429" aria-expanded="true"><div class="accordion-toggle"><span style="">【参考程序】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-3239426635481c3dfc1ef90950939a4429" class="collapse collapse-content"><p></p> ```C++ #include<cstdio> #include<iostream> #include<cstdlib> using namespace std; int a[10001] = { 1 }, n, total; void search(int, int); void print(int); int main() { cin >> n; search(n, 1); cout << "total=" << total << endl; return 0; } void search(int s, int t) { int i; for (i = a[t - 1]; i <= s; i++) { if (i < n) //当前数i要大于前1为数,且不超过n { a[t] = i; //保存当前拆分的数i s -= i; //当s==0时,拆分结束输出结果 if (s == 0) print(t);//当s>0时,继续递归 else search(s, t + 1); s += i; //回溯:加上拆分的数,以便产生说有可能的拆分 } } } void print(int t) { cout << n << "="; for (int i = 1; i <= t - 1; i++) //输出一种拆分方法 cout << a[i] << "+"; cout << a[t] << endl; total++; //方案数累加 1 } ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-f391b6570426790ce8c93e0d7e264fba31" aria-expanded="true"><div class="accordion-toggle"><span style="">【输出结果】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-f391b6570426790ce8c93e0d7e264fba31" class="collapse collapse-content"><p></p>  <p></p></div></div></div> ### 例4:八皇后 <div class="tip inlineBlock info"> 八皇后问题:要在国际象棋棋盘中方八个皇后,使任意两个皇后都不能互相通吃。 (提示:皇后能吃同一行、同一列、同一对角线的任意棋子。) 放置第i个(行)皇后的算法为: ```C++ void search(i) { int j; for (第i个皇后的位置 j = 1; j <= 8; j++) //在本行的8列中去试 { if (本行列允许放置皇后) { 放置第i个皇后; 对放置皇后的位置进行标记; if (i == 8) 输出; //已经放完八个皇后 else search(i + 1); 对放置皇后的位置释放标记,尝试下一个位置是否可行; } } } ``` </div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-3b7854cfc5ff20696bb9c6702649918250" aria-expanded="true"><div class="accordion-toggle"><span style="">【算法分析】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-3b7854cfc5ff20696bb9c6702649918250" class="collapse collapse-content"><p></p> 显然问题的关键在于如何判定某个皇后所在的行、列、斜线上是否有别的皇后;可以从矩阵的特点上找到规律,如果在同一行,则行号相同;如果在同一列上,则列号相同;如果同在/斜线上,则行列值之和相同;如果在\斜线上,则行列只差相同;从图可验证: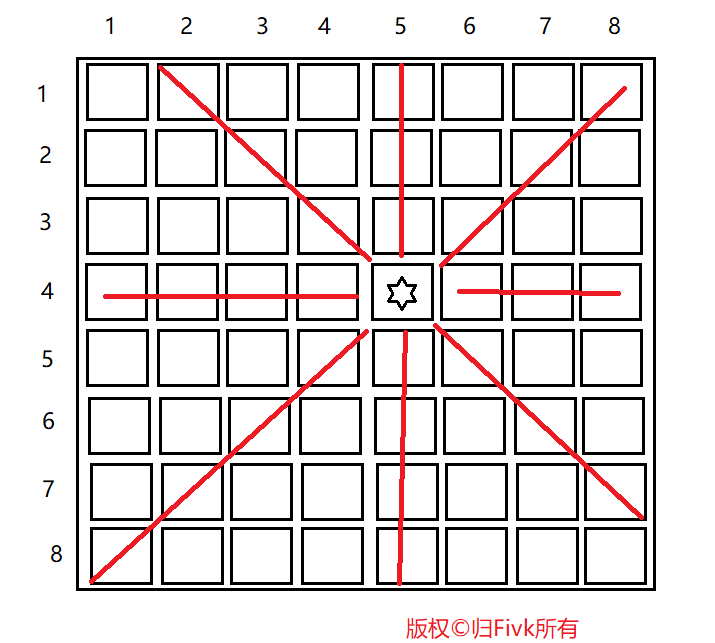 考虑每行有且仅有一个皇后,设一维数组a[1~8]表示皇后放置位置:第i行皇后放在第j列,用a[i]=j来表示,即下标是行数,内容是列数。例如a[3]=5就表示第3个皇后在第3行第5列上。 判断皇后是否安全,即检查同一列、同一对角线是否已有皇后,建立标志数组b[1 ~ 8]控制同一列只能有一个皇后,若两个皇后在同一对角线上,则其他行列坐标之和或坐标只差相等,故亦可建立标志数组,c[1 ~ 16]、d[-7 ~ 7]控制同一对角线上只能有一个皇后。 如果斜线不分方向,则同一斜线上两皇后的行号之差的绝对值之差相同。在这种方式下,要表示两个皇后 i 和 j 不在一列或斜线上的条件可以表述为: ```C++ (a[i]!=a[j)&&(abs(i-j))!=abs(a[i]-a[j]) //i 和 j 分别表示两个皇后的行号 ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-8e24fa4134f1e73a7ef2bff5aee529d589" aria-expanded="true"><div class="accordion-toggle"><span style="">【参考程序】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-8e24fa4134f1e73a7ef2bff5aee529d589" class="collapse collapse-content"><p></p> ```C++ #include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> using namespace std; bool d[17] = { 0 }, b[9] = { 0 }, c[17] = { 0 }; int sum = 0, a[9]; void search(int); void print(); int main() { search(1); //从第 1 个皇后开始放置 return 0; } void search(int i) { int j; for (j = 1; j <= 8; j++) //每个皇后都有8个位置(列)可以式放 if ((!b[j]) && (!c[i + j]) && (!d[i - j + 7])) //寻找放置皇后的位置 //由于C++不能操作负数组,因此考虑加 7 { //摆放皇后,建立相应标志值 a[i] = j; //摆放皇后 b[j] = 1; //宣布占领第j列 c[i + j] = 1; //占领 两个对角线 d[i - j + 7] = 1; //由于C++不能操作负数组,因此考虑加 7 if (i == 8) print(); //8个皇后都放置好,输出 else search(i + 1); //继续递归放置下一个皇后 b[j] = 0; c[i + j] = 0; d[i - j + 7] = 0; } } void print() { int i; sum++; //方案数累加 1 cout << "sum=" << sum << endl; for (i = 1; i <= 8; i++) //输出一种方案 cout << setw(4) << a[i]; cout << endl; } ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-a0c8784288f02994bd247752ae750a9712" aria-expanded="true"><div class="accordion-toggle"><span style="">【输出结果】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-a0c8784288f02994bd247752ae750a9712" class="collapse collapse-content"><p></p> 现在给你看了哦,八皇后问题有92种解。也是大一上,我现在也刚刚大一下嘛,当时读完题目感觉收到降维打击。qvq  <p></p></div></div></div> ### 例5:马的遍历 <div class="tip inlineBlock info"> 中国象棋半张象棋盘如图所示。  马自左下角往有上角跳。今规定只许往右跳,不许往左跳。比如按照图中一种跳行路线,并将所经路线打印出来。打印格式为: 0,1 -> 2,1 -> 3,3 -> 1,4 ->3,5 ->2,7 -> 4,8 ...... </div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-21ff0cf265c97f7711a7302dec375b5e90" aria-expanded="true"><div class="accordion-toggle"><span style="">【算法分析】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-21ff0cf265c97f7711a7302dec375b5e90" class="collapse collapse-content"><p></p>  如图,马最多有四个方向,若原来的横坐标为j、纵坐标为i,则四个方向的移动可表示为: 1. (i,j) -> (i+2,j+1) (i<3,j<8) 2. (i,j) -> (i+1,j+2) (i<4,j<7) 3. (i,j) -> (i-1,j+2) (i>0,j<7) 4. (i,j) -> (i-2,j+1) (j>1,j<8) 搜索策略: 1. a[1]=(0,0); 2. 从a[1]出发,按移动规则依次选定某个方向,如果达到的是(4,8)则打印路径,否则继续搜索下一个到达的顶点。 <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-4dacc19331717191a94294ad9f0cd1ef82" aria-expanded="true"><div class="accordion-toggle"><span style="">【参考程序】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-4dacc19331717191a94294ad9f0cd1ef82" class="collapse collapse-content"><p></p> ```C++ #include<cstdio> #include<iostream> #include<cstdlib> using namespace std; int a[100][3], t = 0; //路径总数和路径 int x[4] = { 2,1,-1,-2 }, y[4] = { 1,2,2,1 }; //四种移动规律 void search(int); //搜索 void print(int); //打印 int main() { a[1][1] = 0; a[1][2] = 0; //从坐标(0,0)开始往右跳第二步 search(2); cout << "count = " << t; return 0; } void search(int i) { for (int j = 0; j <= 3; j++) //往4个方向跳 { if (a[i - 1][1] + x[j] >= 0 && a[iz - 1][1] + x[j] <= 4 && a[i - 1][2] + y[j] >= 0 && a[i - 1][2] + y[j] <= 8) //判断马不越界 { a[i][1] = a[i - 1][1] + x[j]; //保留当前马的位置 a[i][2] = a[i - 1][2] + y[j]; if (a[i][1] == 4 && a[i][2] == 8) print(i); else search(i + 1); //搜索下一步 } } } void print(int n) { int i; t++; for (i = 1; i < n; i++) cout << a[i][1] << ',' << a[i][2] << " -> "; cout << "4,8" << endl; } ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-a8fd87f51b1c5138e03b5c2325d7636f91" aria-expanded="true"><div class="accordion-toggle"><span style="">【输出结果】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-a8fd87f51b1c5138e03b5c2325d7636f91" class="collapse collapse-content"><p></p> 这个是我学习前面几个题后,我自己写出来的第一个回溯题,当时写出来真的好高兴。  <p></p></div></div></div> ### 例6:工作效益 <div class="tip inlineBlock info"> 设有A、B、C、D、E五人从事J1、J2、J3、J4、J5 五项工作,每人只能从事一项,他们的效益如图所示 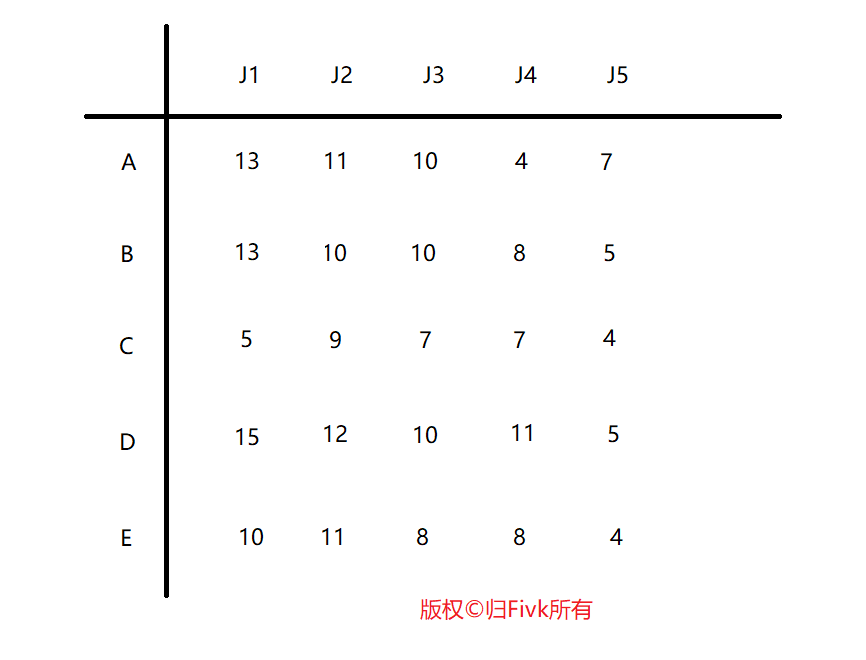 每个人选择 五项工作中的一种,在各种选择的组合中,找到效益最高的一种组合输出。 </div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-8bdea1e5ae32430057036f6c9e9c8ced68" aria-expanded="true"><div class="accordion-toggle"><span style="">【算法分析】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-8bdea1e5ae32430057036f6c9e9c8ced68" class="collapse collapse-content"><p></p> 一、用数组f储存搜索中 工作选择的方案;数组g存放最优的工作选择方案;数组p用于表示某项工作有没有被选择了。 二、 1. 选择p[i]=0的第i项工作 2. 判断效益是否高于max已记录的效益,若高于则更新g数组及max的值。 3. 搜索策略:回溯法(深度优先搜索dfs)。 <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-c27309a33ffa3a1b82b748265ccb05f958" aria-expanded="true"><div class="accordion-toggle"><span style="">【参考程序】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-c27309a33ffa3a1b82b748265ccb05f958" class="collapse collapse-content"><p></p> ```C++ #include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> using namespace std; int data[6][6] = { {0,0,0,0,0,0}, {0,13,11,10,4,7}, {0,13,10,10,8,5}, {0,5,9,7,7,4}, {0,15,12,10,11,5}, {0,10,11,8,8,4} }; int max1 = 0, g[10], f[10]; bool p[6] = { 0 }; void go(int step, int t) //step是第几个人,t是之前已得的效益 { for (int i = 1; i <= 5; i++) if (!p[i]) { //判断第i项工作没人选择 f[step] = i; //第step个人,就选第i项工作 p[i] = 1; //标记第i项工作被人安排了 t += data[step][i]; //计算效益值 if (step < 5) go(step + 1, t); else if (t > max1) { max1 = t; for (int j = 1; j <= 5; j++) g[j] = f[j]; //保存最优效益下的工作选择方案 } t -= data[step][i]; //回溯 p[i] = 0; } } int main() { go(1, 0); for (int i = 1; i <= 5; i++) cout << char(64 + i) << ":J" << g[i] << setw(3); //输出各项工作安排情况 cout << endl; cout << "supply:" << max1 << endl; //输出最佳效益值 } ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-b5cdcbc461caae5e96d301195fcb1f9a2" aria-expanded="true"><div class="accordion-toggle"><span style="">【输出结果】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-b5cdcbc461caae5e96d301195fcb1f9a2" class="collapse collapse-content"><p></p> 这个不知道对没对,应为是我上个星期做的题了,应该是没对,应为如果对了我因该会记得很清楚,但是写了。  <p></p></div></div></div> ### 例7:选书 <div class="tip inlineBlock info"> 放寒假时,信息学竞赛辅导老师有A、B、C、D、E 五本书,要分给参加培训的张、王、刘、孙、李五位同学,每个人只能选一本书。老师先让每个人将自己喜欢的书填在如下的表格中,然后根据他们填写的表来分配书本,希望设计一个程序帮助老师求出所有可能的分配方案,使每个学生都满意。 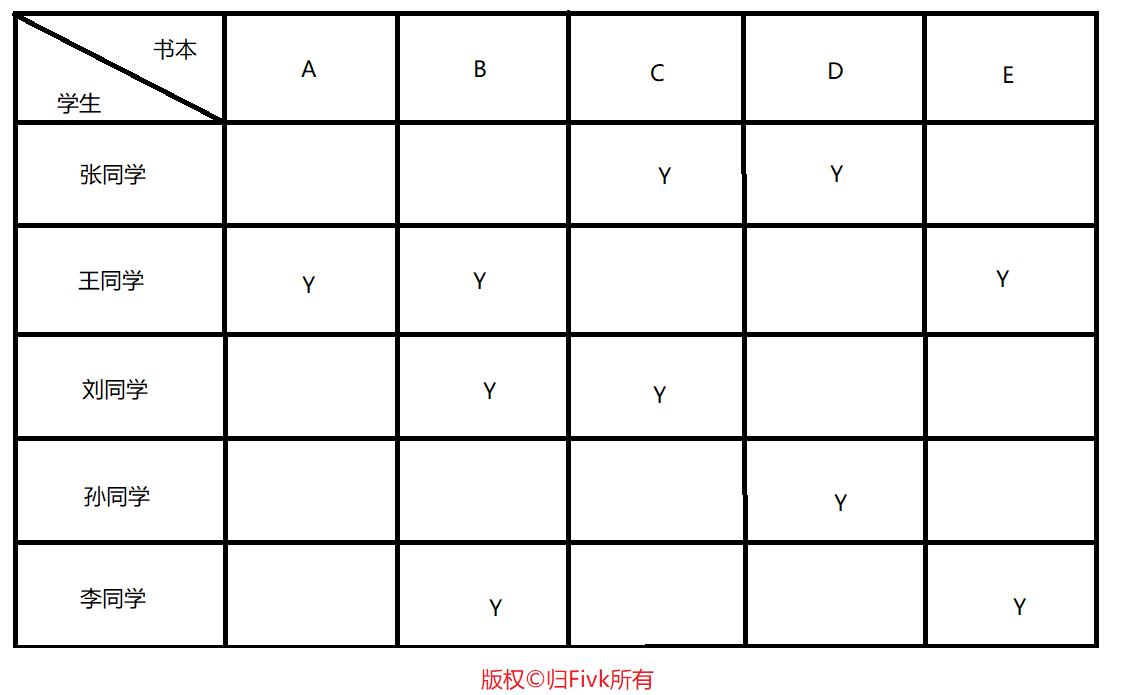 </div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-62726017be6258d04ee3ecca49fdb1d683" aria-expanded="true"><div class="accordion-toggle"><span style="">【算法分析】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-62726017be6258d04ee3ecca49fdb1d683" class="collapse collapse-content"><p></p> 可用穷举法,先不考虑“每个人都满意”这一条件,这样只剩“每个人选一本且只能选一本”这一条件。在这个条件下,可行解就是五本书所有的全排列,一共有5!=120种。然后在这120种可行解中一一删去不符合“每个人都满意”的解,留下的就是本题的解答。 为了编程方便,设1、2、3、4、5分别表示这五本书。这五个数的一种全排列就是五本书的一种分发。例如54321就表示第5本书(即E)分给张,第四种书(即D)分给王,... ,第1本书(即A)分给李。“喜爱1书表”可以用二维数组来表示,1表示喜爱,0表示不喜爱。 算法设计: * S1:产生5个数字的一个全排列; * S2:检查是否符合“喜爱书表”的条件,如果符合就打印出来; * S3:检查是否所有的排列都产生了,如果没有产生完,则返回S1; * S4:结束。 上述算法可能有可以改进的地方。比如产生了一个全排列12345,从中可以看出,选第一本即给张同学的书,1是不可能的,应为张同学只喜欢第3、4本书。这就是说,1XXXX一类的分发都是不符合条件的。由此想到,如果选定第一本书后,就立即检查下一位是否符合条件。例如,第一个数选3,第二个数选4后,立即检查,发现不符合条件,就应该另选第二个数。这样就把34XXX一类的分发在产生前就删去了,又减少一部分运算量。 综上所述,改进后的算法应该是:在产生排列时,每增加一个数,就检查该数是否符合条件,不符合,就立即换下一个,符合条件后,再产生下一个数。应为从第i本数到第到第i本书的寻找过程时相同的,所以可以用回溯算法。算法设计如下: ```C++ int search(i) { for (j = 1; j <= 5; j++) { if (第i个同学给第 j 本书符合条件) { 记录第i个数 if (i == 5) 打印一个解; else search(i + 1); 删去第 i 个数 } } } ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-74bad3bcbe28c67d336d0469a9305ad797" aria-expanded="true"><div class="accordion-toggle"><span style="">【参考程序】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-74bad3bcbe28c67d336d0469a9305ad797" class="collapse collapse-content"><p></p> ```C++ #include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> using namespace std; int book[6], c; bool flag[6], like[6][6] = { {0,0,0,0,0,0}, {0,0,0,1,1,0}, {0,1,1,0,0,1}, {0,0,1,1,0,0}, {0,0,0,0,1,0}, {0,0,1,0,0,1} }; void search(int i); void print(); int main() { search(1); //从第1个开始选书,递归 return 0; } void search(int i) //递归函数 { for (int j = 1; j <= 5; j++) //每个人有5本书可选 if (!flag[j] && like[i][j]) //满足分书的条件 { flag[j] = 1; //把选中的书放入集合flag中,避免重复被选 book[i] = j; //保存的i个人选中的第j本书 if (i == 5) print(); //i==5时所有的人都分到书,输出结果 else search(i + 1); //i<5时,继续递归分书 flag[j] = 0; //回溯:把选中的书放回,产生其他分书的方案 } } void print() { c++; //方案书累加1 cout << "answer " << c << ":\n"; for (int i = 1; i <= 5; i++) cout << i << ": " << char(64 + book[i]) << endl; //输出分书的算法 } ``` <p></p></div></div></div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-1ab5f19b3656d7a82cade5778fc1368c59" aria-expanded="true"><div class="accordion-toggle"><span style="">【输出结果】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-1ab5f19b3656d7a82cade5778fc1368c59" class="collapse collapse-content"><p></p> 这个我是对了的,哈哈哈哈,应为我刚刚写出来了就来更新博客呀,,,,^_^ 我都是篇博客更新很久的,,,这篇博客是3月21日发布的可是现在已经4月4号凌晨了。 是不是博主学的好慢哦~ 主要是都是在周末写的博客。 就先这样了,还有一个题,明天在更新哈哈哈哈。 晚安~~  <p></p></div></div></div> ### 例8:跳马问题 <div class="tip inlineBlock info"> 在5*5格的棋盘上有一个中国象棋的马,从(1,1)点出发,按日字跳马,它可以朝8个方向跳,但不允许出界或跳到已跳过的格子上,要求马跳遍整个棋盘,输出跳的顺序。 </div> <div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-aabbf312f3f850dcaa4fb70f87923aba60" aria-expanded="true"><div class="accordion-toggle"><span style="">【参考程序】</span> <i class="pull-right fontello icon-fw fontello-angle-right"></i> </div> </div> <div class="panel-body collapse-panel-body"> <div id="collapse-aabbf312f3f850dcaa4fb70f87923aba60" class="collapse collapse-content"><p></p> 这是书上的: ```C++ #include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> using namespace std; int u[8] = { 1,2,2,1,-1,-2,-2,-1 }, v[8] = { -2,-1,1,2,2,1,-1,-2 }; //8个方向的x,y增量 int a[100][100] = { 0 }, num = 0; //记每一步走在象棋的哪一格和棋盘的每一格有没有被走过 bool b[100][100] = { 0 }; void search(int, int, int); //以每一格为阶段,在每一阶段中试遍8个方向 void print(); //打印方案 int main() { a[1][1] = 1, b[1][1] = 1; search(1, 1, 2); cout << num << endl; } void search(int i, int j, int n) { int k, x, y; //这三个数一定要定义为局部变量 if (n > 25) { print(); //达到最大规模打印、统计方案 return; } else { for (k = 0; k <= 7; k++) { x = i + u[k]; y = j + v[k]; if (x <= 5 && x >= 1 && y <= 5 && y >= 1 && (!b[x][y])) { //如果新坐标轴在棋盘上,并且这一格可以走 b[x][y] = 1; a[x][y] = n; search(x, y, n + 1); //从(x,y)去搜下一步 b[x][y] = 0; a[x][y] = 0; } } } } void print() { num++; if (num <= 5) //统计总方案 { for (int k = 1; k <= 5; k++) //打印出前5种方案 { for (int kk = 1; kk <= 5; kk++) //打印本次方案 { cout << setw(5) << a[k][kk]; } cout << endl; } } } ``` 我刚刚写的:运行时间短一点哈哈哈哈 ```C++ #include<stdio.h> int a[6][6]={0}; int count=2; int number=0; const int dx[]={0,1,2,2,1,-1,-2,-2,-1}; const int dy[]={0,2,1,-1,-2,-2,-1,1,2}; void dfs(int x,int y); void print(); int main(void) { a[1][1]=1; dfs(1,1); printf("\n\n number = %d\n",number); return 0; } void dfs(int x,int y) { int i,j; for(i=1;i<=8;i++) { if(x+dx[i]>=1&&x+dx[i]<=5&&y+dy[i]>=1&&y+dy[i]<=5&&(!a[x+dx[i]][y+dy[i]])) { x+=dx[i]; y+=dy[i]; a[x][y]=count; count++; if(count==26) { print(); }else{ dfs(x,y); } count--; a[x][y]=0; x-=dx[i]; y-=dy[i]; } } } void print() { number++; if(number<=5) for(int i=1;i<=5;i++) { for(int j=1;j<=5;j++) { printf("%3d ",a[i][j]); } printf("\n"); } } ``` <p></p></div></div></div> <div class="tip inlineBlock success"> 到这里已经更新完了,这一篇文章更新这么久^_^ 14天,两周。qvq </div> 最后修改:2022 年 03 月 11 日 © 禁止转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏
3 条评论
666OωO
好东西呀,记得还是挺详细的,对新手来说挺友好的,博主666|´・ω・)ノ