Loading... ### 1.区间合并 一共有 `n` 个数,编号是 `1∼n`,最开始每个数各自在一个集合中。 现在要进行 `m` 个操作,操作共有两种: 1. `M a b`,将编号为 `a` 和 `b` 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作; 2. `Q a b`,询问编号为 `a` 和 `b` 的两个数是否在同一个集合中; #### 输入格式 第一行输入整数 `n` 和 `m`。 接下来 `m` 行,每行包含一个操作指令,指令为 `M a b`或`Q a b` 中的一种。 #### 输出格式 对于每个询问指令 `Q a b`,都要输出一个结果,如果 `a` 和 `b` 在同一集合内,则输出 `Yes`,否则输出 `No`。 每个结果占一行。 #### 数据范围 $1≤n,m≤10^5$ #### 输入样例: ```in 4 5 M 1 2 M 3 4 Q 1 2 Q 1 3 Q 3 4 ``` #### 输出样例: ```out Yes No Yes ``` ### 2.思路 #### 并查集 从代码的角度分析 #### 初始化 ```cpp for(int i = 1; i <= n; i ++) p[i] = i; ``` 上面的代码实现的结果如下图所示  很容易理解,就是将当前数据的父节点指向自己。就是说最开始每个元素都是一个集合,每个集合只有最开始自己一个元素。 #### 查找 + 路径压缩 ```cpp int find(int x){ //返回x的祖先节点 + 路径压缩 //祖先节点的父节点是自己本身 if(p[x] != x){ //将x的父亲置为x父亲的祖先节点,实现路径的压缩 p[x] = find(p[x]); } return p[x]; } ``` <div class="tip inlineBlock info simple"> `find`的功能是用于查找祖先节点,那么路径压缩又是怎么完成的 </div>  注意图,当我们在查找`1`的父节点的过程中,路径压缩的实现 针对 `x = 1` <div class="tip inlineBlock success simple"> find(1) p[1] = 2 p[1] = find(2) find(2) p[2] = 3 p[2] = find(3) find(3) p[3] = 4 p[3] = find(4) find(4) p[4] = 4 将p[4]返回 退到上一层 find(3) p[3] = 4 p[3] = 4 将p[3]返回 退到上一层 find(2) p[2] = 3 p[2] = 4 将p[2]返回 退到上一层 find(1) p[1] = 2 p[1] = 4 将p[1]返回 至此,我们发现所有的1,2,3的父节点全部置为了4,实现路径压缩;同时也实现了1的父节点的返回 nice!! </div> #### 合并操作 ```cpp if(op == 'M') p[find(a)] = find(b); //将a的祖先点的父节点置为b的祖先节点 ``` 假设有两个集合 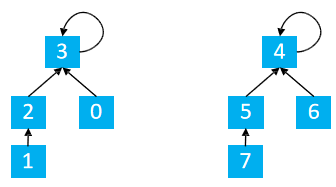 合并1, 5 find(1) = 3 find(5) = 4 p[find(1)] = find(5) –> p[3] = 4 如下图所示 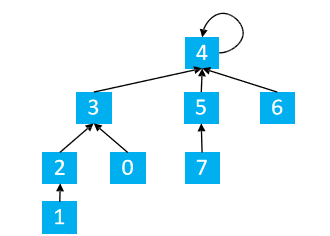 #### 查找 ```cpp if (find(a) == find(b)) puts("在同一个集合中"); else puts("不在同一个集合"); ``` #### 其他路径压缩方法 1. 路径分裂:使路径上的每个节点都指向其祖父节点(parent的parent) 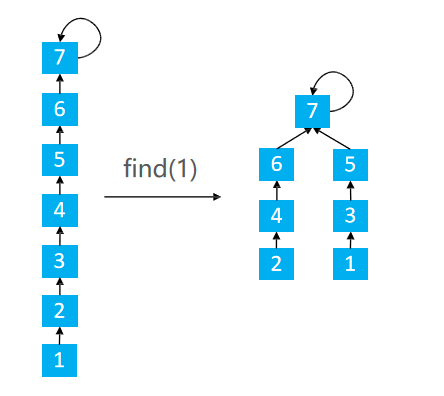 ```cpp int find(int x){ while(x != p[x]){ int parent = p[x]; p[x] = p[p[x]]; x = parent; } return x; } ``` 2. 路径减半:使路径上每隔一个节点就指向其祖父节点(parent的parent) 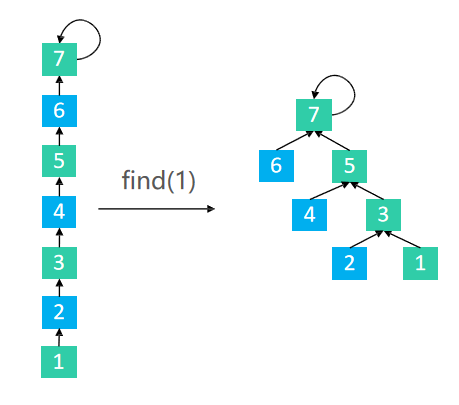 ```cpp int find(int x){ while(x != p[x]){ p[x] = p[p[x]]; x = p[x]; } return x; } ``` ### 3.总结 并查集 1. 将两个集合合并 2. 询问两个元素是否在一个集合中 <div class="tip inlineBlock share simple"> 基本原理:每个集合用一棵树来表示。树的编号就是整个集合的编号。每个节点存储它的父节点,`p[x]`表示`x`的父节点 </div> 1. 判断树根 `if(p[x] = x)` 2. 求x的集合编号 `while(p[x] != x) x = p[x]` 3. 合并两个集合,这两将x的根节点嫁接到y的根节点, `px`为`x`的根节点, `py`为`y`的根节点,嫁接`p[px] = py` ### 4.C++代码 ```cpp #include <iostream> using namespace std; const int N = 1e5 + 10; int p[N]; int n, m; void init() { for (int i = 1; i <= n; i ++) p[i] = i; } int find(int x) { // 返回x的祖宗节点 + 路径压缩 if (p[x] != x) p[x] = find(p[x]); return p[x]; } int main() { cin >> n >> m; init(); while (m --) { char op; int a, b; cin >> op >> a >> b; if (op == 'M') { p[find(a)] = find(b); // a的祖宗节点的父节点等于b的祖宗节点 } else { if (find(a) == find(b)) puts("Yes"); else puts("No"); } } return 0; } ``` ### 4.变形 #### 连通块中点的数量 给定一个包含 `n` 个点(编号为 `1∼n`)的无向图,初始时图中没有边。 现在要进行 `m` 个操作,操作共有三种: 1. `C a b`,在点 `a` 和点 `b` 之间连一条边,`a` 和 `b` 可能相等; 2. `Q1 a b`,询问点 `a` 和点 `b` 是否在同一个连通块中,`a` 和 `b` 可能相等; 3. `Q2 a`,询问点 `a` 所在连通块中点的数量; #### 输入格式 第一行输入整数 n 和 `m`。 接下来 `m` 行,每行包含一个操作指令,指令为 `C a b`,`Q1 a b`或`Q2 a` 中的一种。 #### 输出格式 对于每个询问指令 `Q1 a b`,如果 `a` 和 `b` 在同一个连通块中,则输出 `Yes`,否则输出 `No`。 对于每个询问指令 `Q2 a`,输出一个整数表示点 `a` 所在连通块中点的数量 每个结果占一行。 #### 数据范围 $1≤n,m≤10^5$ #### 输入样例: ```cpp 5 5 C 1 2 Q1 1 2 Q2 1 C 2 5 Q2 5 ``` #### 输出样例: ```cpp Yes 2 3 ``` ### 5.分析 因为与合并题目中唯一不同的是,多了记录合并集合中连通块的个数 通过size数组记录以当前点x为祖先节点的集合中的连通块个数 ```cpp for(int i = 1; i <= n; i ++) { p[i] = i; //用祖先节点记录当前合并集合的size size[i] = 1; } ``` 初始化,让自己指向自己,同时标记自己为祖先节点下,有多少个连通块,初始为1 <div class="tip inlineBlock warning simple"> 什么时候改变连通块的个数呢?容 </div> <div class="tip inlineBlock success"> 合并的时候 </div> 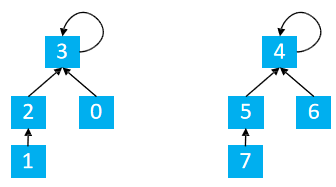 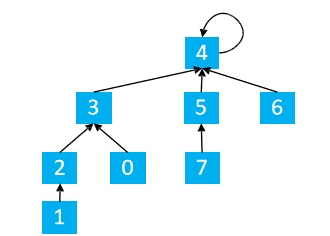 <div class="tip inlineBlock success simple"> 显然,将1,5合并 find(1) = 3 find(5) = 4 p[3] = 4 这时候有8个点相连接 合并的数目更新方式: size[3] = 4 以3为根节点下有4个连通块 size[4] = 4 以4为根节点下有4个连通块 更新4节点的连通块情况 size[4] = size[4] + size[3] = 8 </div> ### C++代码 ```cpp #include <iostream> using namespace std; const int N = 1e5 + 10; int n, m; int p[N], cnt[N]; void init() { for (int i = 1; i <= n; i ++) { p[i] = i; cnt[i] = 1; } } int find(int x) { if (p[x] != x) p[x] = find(p[x]); return p[x]; } int main() { cin >> n >> m; init(); string op; int a, b; while (m --) { cin >> op; if (op == "C") { cin >> a >> b; a = find(a), b = find(b); if (a != b) { p[a] = b; cnt[b] += cnt[a]; } } else if (op == "Q1") { cin >> a >> b; if (find(a) == find(b)) puts("Yes"); else puts("No"); } else { cin >> a; cout << cnt[find(a)] << endl; } } return 0; } ``` 最后修改:2022 年 04 月 15 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 2 如果觉得我的文章对你有用,请随意赞赏