【R语言】均值向量检测

博主： Fivk
发布时间：2022 年 03 月 17 日
906 次浏览
暂无评论
4437字数
分类：代码笔记

# 1、测定稻谷每亩穗数X1,每穗粒数X2,每亩稻谷产量X3，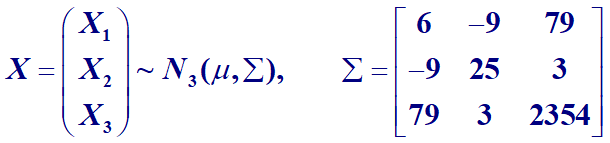

![](https://blog.fivk.cn/usr/uploads/2022/03/3009594751.png)

| X1 | 26.7 | 31.3 | 30.4 | 33.9 | 34.6 | 33.8 | 30.4 | 27   | 33.3 | 30.4 | 31.5 | 33  | 34   |
| ---- | ------ | ------ | ------ | ------ | ------ | ------ | ------ | ------ | ------ | ------ | ------ | ----- | ------ |
| X2 | 73.4 | 59   | 65.9 | 58.2 | 64.6 | 64.6 | 62.1 | 71.4 | 64.5 | 64.1 | 61.1 | 56  | 59.8 |
| X3 | 1008 | 959  | 1051 | 1022 | 1097 | 1103 | 992  | 945  | 1074 | 1029 | 1004 | 995 | 1045 |

检验均值是否等于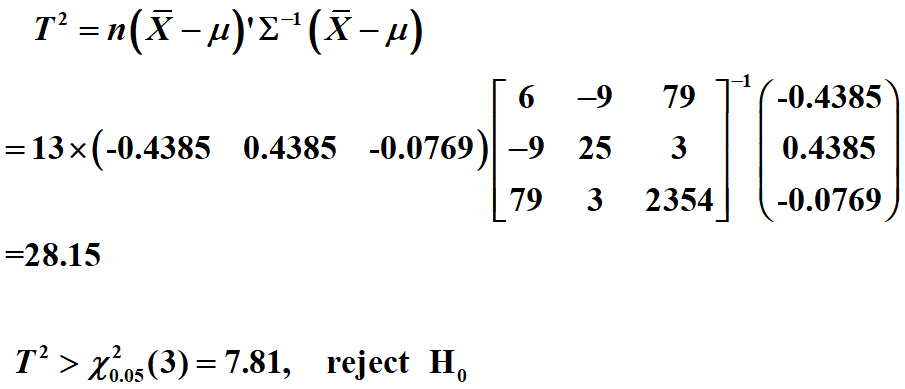

![](https://blog.fivk.cn/usr/uploads/2022/03/4172729420.png)

### 参考

![](https://blog.fivk.cn/usr/uploads/2022/03/391138813.png)

![](https://blog.fivk.cn/usr/uploads/2022/03/1850286423.png)

### 练习

在企业市场结构研究中，起决定作用的指标有市场份额X1，企业规模（资产净值总额的自然对数）X2，资本收益率X3和总收益增长率X4。为了研究美国市场的变动，夏菲尔德抽取了美国231个大型企业，调查这些企业某十年的资料。假设以前企业市场结构的均值向量为(20,7.5,10,2)’，该调查所得的样本均值向量和总体协方差矩阵如下。

$$
\overline{X}=(20.92,8.06,11.78,1.090)

$$
{\Sigma}=\left(
\begin{matrix}
0.26 & 0.08 & 1.639 & 0.156  \\
0.08 & 1.513 & -0.222 & -0.019  \\
1.639 & -0.222 & 26.626 & 2.233  \\
0.156 & -0.019 & 2.233 & 1.346
\end{matrix}
\right)

试问企业的市场结构是否发生了变化？

答：根据题意

假设$u=u_0$

$$
u_0=(20,7.5,10,2)

$$
\overline{X}-u_0=(0.92,0.56,1.78,-0.91)

$$
{\Sigma}=\left(
\begin{matrix}
0.26 & 0.08 & 1.639 & 0.156  \\
0.08 & 1.513 & -0.222 & -0.019  \\
1.639 & -0.222 & 26.626 & 2.233  \\
0.156 & -0.019 & 2.233 & 1.346
\end{matrix}
\right)

我们可以根据$T^2=n(\overline{X}-u_0)^{'}{\Sigma}^{-1}(\overline{X}-u_0)$

计算得到

$$
T^2=231{\times}(0.92,0.56,1.78,-0.91)^{'}\left(
\begin{matrix}
0.26 & 0.08 & 1.639 & 0.156  \\
0.08 & 1.513 & -0.222 & -0.019  \\
1.639 & -0.222 & 26.626 & 2.233  \\
0.156 & -0.019 & 2.233 & 1.346
\end{matrix}
\right)\left(
\begin{matrix}
0.92\\
0.56\\
1.78\\
-0.91
\end{matrix}
\right)=1248.096

因为

$$
T^2=1248.096{\geqslant}{\chi}^2_{0.05}=9.487729

故拒绝原假设，企业的市场结构发生了变化。

# 2、 某种产品有甲乙两个品牌

从两种品牌的产品中分别抽出5个，质量指标X包含5个指标，服从多元正态分布，且甲乙两个品牌的协方差阵相同。指标数据如下：

| 序号 | X1 | X2 | X3 | X4 | X5 |
| ------ | ---- | ---- | ---- | ---- | ---- |
| 1    | 11 | 18 | 15 | 18 | 15 |
| 2    | 33 | 27 | 31 | 21 | 17 |
| 3    | 20 | 28 | 27 | 23 | 19 |
| 4    | 18 | 26 | 18 | 18 | 9  |
| 5    | 22 | 23 | 22 | 16 | 10 |

| 序号 | X1 | X2 | X3 | X4 | X5 |
| ------ | ---- | ---- | ---- | ---- | ---- |
| 1    | 18 | 17 | 20 | 18 | 18 |
| 2    | 31 | 24 | 31 | 26 | 20 |
| 3    | 14 | 16 | 17 | 20 | 17 |
| 4    | 25 | 24 | 31 | 26 | 18 |
| 5    | 36 | 28 | 24 | 26 | 29 |

检验两种品牌的质量指标差异有显著不同。

**解 假设检验类型为∶** $H_0:{\mu}_x-{\mu}_y=0$ $\leftrightarrow$ $H_1:{\mu}_x-{\mu}_y{\neq}0$

$$
\overline{x}=\left[
\begin{matrix}
20.8 \\
24.4 \\
22.6 \\
19.2 \\
14.0
\end{matrix} \right]_, \ \ \ \ \overline{y}=\left[
\begin{matrix}
24.8 \\
21.8 \\
24.6 \\
23.2 \\
20.4
\end{matrix} \right], \ \ \ \ \overline{x}-\overline{y}=\left[
\begin{matrix}
-4.0 \\
2.6 \\
-2.0 \\
-4.0 \\
-6.4
\end{matrix} \right]

$$
A_1=\left[
\begin{matrix}
11 & 18 & 15 & 18 & 15 \\
33 & 27 & 31 & 21 & 17 \\
20 & 28 & 27 & 23 & 19 \\
18 & 26 & 18 & 18 & 9  \\
22 & 23 & 22 & 16 & 10
\end{matrix} \right]_, \ \ \ \ \ A_2=\left[
\begin{matrix}
18 & 17 & 20 & 18 & 18 \\
31 & 24 & 31 & 26 & 20 \\
14 & 16 & 17 & 20 & 17 \\
25 & 24 & 31 & 26 & 18  \\
36 & 28 & 24 & 26 & 29
\end{matrix} \right], \ \ \ \ \ A_1+A_2=\left[
\begin{matrix}
29 & 64 & 34 & 43 & 58 \\
35 & 51 & 44 & 50 & 51 \\
35 & 62 & 44 & 49 & 46 \\
36 & 47 & 43 & 44 & 42 \\
33 & 37 & 36 & 27 & 39
\end{matrix} \right]

**协方差阵未知但相等（用估计量替代）：**

$$
T^2=\frac{nm}{n+m}(\overline{X}-\overline{Y})^{'}(\frac{A_1+A_2}{n+m-2})^{-1}(\overline{X}-\overline{Y})

$$
\frac{(n_1+n_2-2)-p+1}{p(n_1+n_2-2)}T^2{\leftrightarrow}F^2(p,(n_1+n_2-2)-p+1)

其中

$$
\hat{{\Sigma}}=\frac{L_x+L_y}{n_1+n_2-2}

是协方差${\Sigma}$的估计矩阵。

计算得到

$$
T^2={\frac{5{\times}5}{5+5}}
\begin{pmatrix}
24.8 & 21.8 & 24.6 & 23.2 & 20.4 
\end{pmatrix}\left[{\frac{1}{5+5-2}}\begin{pmatrix}
29 & 64 & 34 & 43 & 58 \\
35 & 51 & 44 & 50 & 51 \\
35 & 62 & 44 & 49 & 46 \\
36 & 47 & 43 & 44 & 42 \\
33 & 37 & 36 & 27 & 39
\end{pmatrix}\right]^{-1}\begin{pmatrix}
24.8 \\ 21.8 \\ 24.6 \\ 23.2 \\ 20.4 
\end{pmatrix}=2165.588

$$
F=\frac{(n_1+n_2-2)-p+1}{p(n_1+n_2-2)}T^2=216.5588{\geq}F_{0.95,4}(5)

拒绝$H_0$

最后修改：2022 年 06 月 05 日