【动态规划】蒙德里安的梦想

博主： Fivk
发布时间：2022 年 01 月 24 日
958 次浏览
2774字数
分类：题目典例

求把 `N×M` 的棋盘分割成若干个 `1×2` 的的长方形，有多少种方案。

例如当 `N=2，M=4` 时，共有 `5` 种方案。当 `N=2，M=3` 时，共有 `3` 种方案。

如下图所示：

![](https://blog.fivk.cn/usr/uploads/2022/01/2230381418.jpg)

#### 输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数 `N` 和 `M`。

当输入用例 `N=0，M=0` 时，表示输入终止，且该用例无需处理。

#### 输出格式

每个测试用例输出一个结果，每个结果占一行。

#### 数据范围

`1≤N, M≤11`

#### 输入样例：

```in
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
```

#### 输出样例：

```out
1
0
1
2
3
5
144
51205
```

#### 算法分析

通过观察发现对于一个`NxM`的棋盘里面，当1x2的长方形横着摆放完之后，竖的也就唯一确定了直接放进去就好了。所以对于题目所求的拜访方式的数量和横着摆放数量相等。

> 摆放方块的时候，先放横着的，再放竖着的。
>
> 总方案数等于只放横着的小方块的合法方案数。

如何判断，当前方案数是否合法？ 所有剩余位置能否填充满竖着的小方块。可以按列来看，每一列内部所有连续的空着的小方块需要是偶数个。

这是一道动态规划的题目，并且是一道 状态压缩的dp：用一个N位的二进制数，每一位表示一个物品，0/1表示不同的状态。因此可以用$0→2^N−1$（N二进制对应的十进制数）中的所有数来枚举全部的状态。

#### 状态表示

状态表示：`f[i][j]` 表示已经将前 `i -1` 列摆好，且从第`i−1`列，伸出到第 `i` 列的状态是 `j` 的所有方案。其中`j`是一个二进制数，用来表示哪一行的小方块是横着放的，其位数和棋盘的行数一致。

#### 状态转移

既然第 `i` 列固定了，我们需要看 第`i-2` 列是怎么转移到到第 `i-1`列的（看最后转移过来的状态）。假设此时对应的状态是k（第`i-2`列到第`i-1`列伸出来的二进制数，比如00100），`k`也是一个二进制数，`1`表示哪几行小方块是横着伸出来的，`0`表示哪几行不是横着伸出来的。

它对应的方案数是 `f[i−1,k]` ，即前`i-2`列都已摆完，且从第`i-2`列伸到第`i-1`列的状态为 `k` 的所有方案数。

这个`k`需要满足什么条件呢?

首先`k`不能和 `j`在同一行（如下图）：因为从`i-1`列到第`i`列是横着摆放的`12`的方块，那么`i-2`列到`i-1`列就不能是横着摆放的，否则就是`13`的方块了！这与题意矛盾。所以 `k`和`j`不能位于同一行。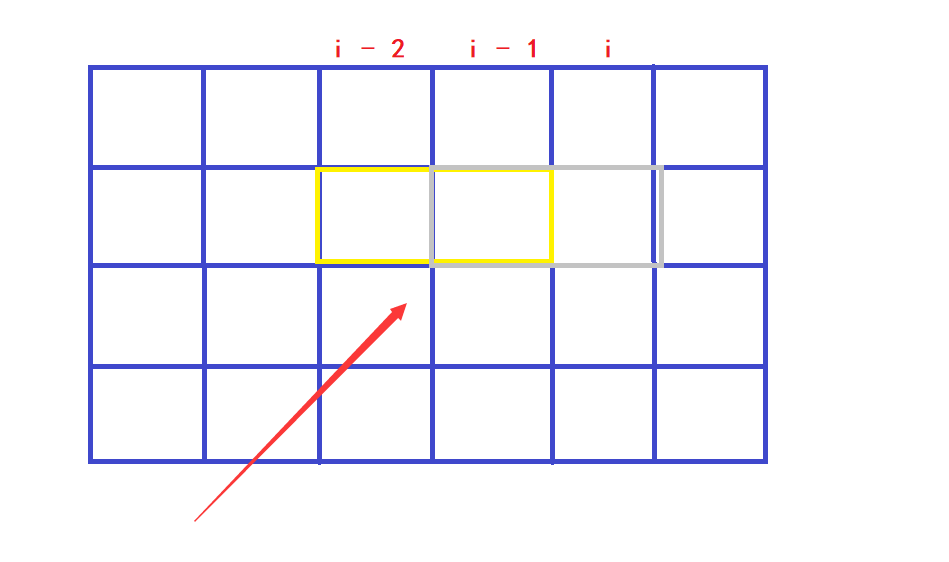

![](https://blog.fivk.cn/usr/uploads/2022/01/3903561710.png)

既然不能同一行伸出来，那么对应的代码为`(k & j ) == 0` ，表示两个数相与，如果有`1`位相同结果就不是0， `(k & j ) == 0`表示 `k`和`j`没有`1`位相同， 即没有`1`行有冲突。

既然从第`i-1`列到第`i`列横着摆的，和第`i-2`列到第`i-1`列横着摆的都确定了，那么第`i-1`列 空着的格子就确定了，这些空着的格子将来用作竖着放。如果 某一列有这些空着的位置，那么该列所有连续的空着的位置长度必须是偶数。

总共`m`列，我们假设列下标从`0`开始，即第`0`列，第`1`列……，第`m-1`列。根据状态表示`f[i][j]` 的定义，我们答案是什么呢？ 请读者返回定义处思考一下。答案是`f[m][0]`， 意思是 前`m-1`列全部摆好,且从第`m-1`列到`m`列状态是`0`（意即从第`m-1`列到第`m`列没有伸出来的）的所有方案，即整个棋盘全部摆好的方案。

#### 时间复杂度

`dp`的时间复杂度 =状态表示× 状态转移

状态表示 `f[i][j]` 第一维`i`可取11，第二维`j`（二进制数）可取`211211` ，所以状态表示 $11×2^11$
状态转移 也是$2^{11}$
所以总的时间复杂度
$11×2^{11}×2^{11}≈4×10^7$

可以过

```cpp
#include<bits/stdc++.h>
using namespace std;

const int N=12, M = 1<< N;

long long f[N][M] ;// 第一维表示列， 第二维表示所有可能的状态

bool st[M];  //存储每种状态是否有奇数个连续的0，如果奇数个0是无效状态，如果是偶数个零置为true。

//vector<int > state[M];  //二维数组记录合法的状态
vector<vector<int>> state(M);  //两种写法等价:二维数组
int m , n;

int main(){

while(cin>>n>>m, n||m){ //读入n和m，并且不是两个0即合法输入就继续读入

//第一部分：预处理1
        //对于每种状态，先预处理每列不能有奇数个连续的0

for(int i=0; i< 1<<n; i++){

int cnt =0 ;//记录连续的0的个数

bool isValid = true; // 某种状态没有奇数个连续的0则标记为true

for(int j=0;j<n;j++){ //遍历这一列，从上到下

if( i>>j &1){  //i>>j位运算，表示i（i在此处是一种状态）的二进制数的第j位； &1为判断该位是否为1，如果为1进入if
                    if(cnt &1) { //这一位为1，看前面连续的0的个数，如果是奇数（cnt &1为真）则该状态不合法
                        isValid =false;break;
                    } 
                    cnt=0; // 既然该位是1，并且前面不是奇数个0（经过上面的if判断），计数器清零。//其实清不清零没有影响
                 }
                 else cnt++; //否则的话该位还是0，则统计连续0的计数器++。
            }
            if(cnt &1)  isValid =false; //最下面的那一段判断一下连续的0的个数

st[i]  = isValid; //状态i是否有奇数个连续的0的情况,输入到数组st中
        }

//第二部分：预处理2
        // 经过上面每种状态 连续0的判断，已经筛掉一些状态。
        //下面来看进一步的判断：看第i-2列伸出来的和第i-1列伸出去的是否冲突

for(int j=0;j< 1<<n;j++){ //对于第i列的所有状态
            state[j].clear(); //清空上次操作遗留的状态，防止影响本次状态。
            for(int k=0;k< 1<<n;k++){ //对于第i-1列所有状态
                if((j&k )==0 && st[ j| k] ) // 第i-2列伸出来的 和第i-1列伸出来的不冲突(不在同一行) 
                //解释一下st[j | k] 
                //已经知道st[]数组表示的是这一列没有连续奇数个0的情况，
                //我们要考虑的是第i-1列（第i-1列是这里的主体）中从第i-2列横插过来的，还要考虑自己这一列（i-1列）横插到第i列的
                //比如 第i-2列插过来的是k=10101，第i-1列插出去到第i列的是 j =01000，
                //那么合在第i-1列，到底有多少个1呢？自然想到的就是这两个操作共同的结果：两个状态或。 j | k = 01000 | 10101 = 11101
                //这个 j|k 就是当前 第i-1列的到底有几个1，即哪几行是横着放格子的

state[j].push_back(k);  //二维数组state[j]表示第j行， 
                    //j表示 第i列“真正”可行的状态，如果第i-1列的状态k和j不冲突则压入state数组中的第j行。
                    //“真正”可行是指：既没有前后两列伸进伸出的冲突；又没有连续奇数个0。
            }

}

//第三部分：dp开始

memset(f,0,sizeof f);  //全部初始化为0，因为是连续读入，这里是一个清空操作。类似上面的state[j].clear()

f[0][0]=1 ;// 这里需要回忆状态表示的定义，按定义这里是：前第-1列都摆好，且从-1列到第0列伸出来的状态为0的方案数。
        //首先，这里没有-1列，最少也是0列。其次，没有伸出来，即没有横着摆的。即这里第0列只有竖着摆这1种状态。

for(int i=1;i<= m;i++){ //遍历每一列:第i列合法范围是(0~m-1列)
            for(int j=0; j< 1<<n; j++){  //遍历当前列（第i列）所有状态j
                for( auto k : state[j])    // 遍历第i-1列的状态k，如果“真正”可行，就转移
                    f[i][j] += f[i-1][k];    // 当前列的方案数就等于之前的第i-1列所有状态k的累加。
            }
        }

//最后答案是什么呢？
        //f[m][0]表示 前m-1列都处理完，并且第m-1列没有伸出来的所有方案数。
        //即整个棋盘处理完的方案数

cout<< f[m][0]<<endl;
    }
}
```

最后修改：2022 年 01 月 24 日

如果觉得我的文章对你有用，请随意赞赏

【动态规划】蒙德里安的梦想

Fivk • 2022 年 01 月 24 日

求把 `N×M` 的棋盘分割成若干个 `1×2` 的的长方形，有多少种方案。

例如当 `N=2，M=4` 时，共有 `5` 种方案。当 `N=2，M=3` 时，共有 `3` 种方案。

如下图所示：

![](https://blog.fivk.cn/usr/uploads/2022/01/2230381418.jpg)

#### 输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数 `N` 和 `M`。

当输入用例 `N=0，M=0` 时，表示输入终止，且该用例无需处理。

#### 输出格式

每个测试用例输出一个结果，每个结果占一行。

#### 数据范围

`1≤N, M≤11`

#### 输入样例：

```in
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
```

#### 输出样例：

```out
1
0
1
2
3
5
144
51205
```

#### 算法分析

> 摆放方块的时候，先放横着的，再放竖着的。
>
> 总方案数等于只放横着的小方块的合法方案数。

如何判断，当前方案数是否合法？ 所有剩余位置能否填充满竖着的小方块。可以按列来看，每一列内部所有连续的空着的小方块需要是偶数个。

#### 状态表示

#### 状态转移

它对应的方案数是 `f[i−1,k]` ，即前`i-2`列都已摆完，且从第`i-2`列伸到第`i-1`列的状态为 `k` 的所有方案数。

这个`k`需要满足什么条件呢?

![](https://blog.fivk.cn/usr/uploads/2022/01/3903561710.png)

#### 时间复杂度

`dp`的时间复杂度 =状态表示× 状态转移

可以过

```cpp
#include<bits/stdc++.h>
using namespace std;

const int N=12, M = 1<< N;

long long f[N][M] ;// 第一维表示列， 第二维表示所有可能的状态

bool st[M];  //存储每种状态是否有奇数个连续的0，如果奇数个0是无效状态，如果是偶数个零置为true。

//vector<int > state[M];  //二维数组记录合法的状态
vector<vector<int>> state(M);  //两种写法等价:二维数组
int m , n;

int main(){

while(cin>>n>>m, n||m){ //读入n和m，并且不是两个0即合法输入就继续读入

//第一部分：预处理1
        //对于每种状态，先预处理每列不能有奇数个连续的0

for(int i=0; i< 1<<n; i++){

int cnt =0 ;//记录连续的0的个数

bool isValid = true; // 某种状态没有奇数个连续的0则标记为true

for(int j=0;j<n;j++){ //遍历这一列，从上到下

st[i]  = isValid; //状态i是否有奇数个连续的0的情况,输入到数组st中
        }

}

//第三部分：dp开始

memset(f,0,sizeof f);  //全部初始化为0，因为是连续读入，这里是一个清空操作。类似上面的state[j].clear()

//最后答案是什么呢？
        //f[m][0]表示 前m-1列都处理完，并且第m-1列没有伸出来的所有方案数。
        //即整个棋盘处理完的方案数

cout<< f[m][0]<<endl;
    }
}
```

【动态规划】蒙德里安的梦想

【踩坑日志】SpringBoot项目启动提示This primary key of "id" is primitive !不建议如此请使用包装类 in Class:

【C】极域电子教室学生端解除控制

【开发技巧】@CrossOrigin注解解决跨域问题

这是好东西

【Fivk】文章归档

【项目实战】探花交友项目实战

【Linux】Linux-Day02

【BT】宝塔专业版授权

【微服务】elasticsearch分布式搜索引擎（中）

我去……

【动态规划】蒙德里安的梦想