Loading... 一个正整数 n 可以表示成若干个正整数之和,形如:$n=n_1+n_2+…+n_k$,其中 $n_1≥n_2≥…≥n_k,k≥1$。 我们将这样的一种表示称为正整数 n 的一种划分。 现在给定一个正整数 n,请你求出 n 共有多少种不同的划分方法。 #### 输入格式 共一行,包含一个整数 n。 #### 输出格式 共一行,包含一个整数,表示总划分数量。 由于答案可能很大,输出结果请对 $10^9+7$ 取模。 #### 数据范围 1≤n≤1000 #### 输入样例: ``` 5 ``` #### 输出样例: ``` 7 ``` #### 分析 **思路**:把`1,2,3, … n`分别看做`n`个物体的体积,这`n`个物体均无使用次数限制,问恰好能装满总体积为`n`的背包的**总方案数**(完全背包问题变形) **初值问题:** 求最大值时,当都不选时,价值显然是 `0` 而求方案数时,当都不选时,方案数是 `1`(即前 `i` 个物品都不选的情况也是一种方案),所以需要初始化为 `1` 即:`for (int i = 0; i <= n; i ++) f[i][0] = 1;`等价变形后:`f[0] = 1` **状态计算:** `f[i][j]` 表示前`i`个整数`(1,2…,i)`恰好拼成j的方案数 求方案数:把集合选`0`个`i`,`1`个`i`,`2`个`i`,…全部加起来 $$ f[i][j] = f[i - 1][j] + f[i - 1][j - i] + f[i - 1][j - 2 * i] + ...; $$ $$ f[i][j - i] = f[i - 1][j - i] + f[i - 1][j - 2 * i] + ...; $$ 因此 $f[i][j]=f[i−1][j]+f[i][j−i];f[i][j]=f[i−1][j]+f[i][j−i];$ (这一步类似完全背包的推导) #### 朴素做法 ```cpp // f[i][j] = f[i - 1][j] + f[i][j - i] #include <iostream> using namespace std; const int N = 1e3 + 7, mod = 1e9 + 7; int f[N][N]; int main() { int n; cin >> n; for (int i = 0; i <= n; i ++) { f[i][0] = 1; // 容量为0时,前 i 个物品全不选也是一种方案 } for (int i = 1; i <= n; i ++) { for (int j = 0; j <= n; j ++) { f[i][j] = f[i - 1][j] % mod; // 特殊 f[0][0] = 1 if (j >= i) f[i][j] = (f[i - 1][j] + f[i][j - i]) % mod; } } cout << f[n][n] << endl; } ``` #### 等价变形 ```cpp // f[i][j] = f[i - 1][j] + f[i][j - i] #include <iostream> using namespace std; const int N = 1e3 + 7, mod = 1e9 + 7; int f[N]; int main() { int n; cin >> n; f[0] = 1; // 容量为0时,前 i 个物品全不选也是一种方案 for (int i = 1; i <= n; i ++) { for (int j = i; j <= n; j ++) { f[j] = (f[j] + f[j - i]) % mod; } } cout << f[n] << endl; } ``` #### 思路2 状态表示: f[i][j]表示总和为i,总个数为j的方案数 状态转移方程: f[i][j] = f[i - 1][j - 1] + f[i - j][j]; 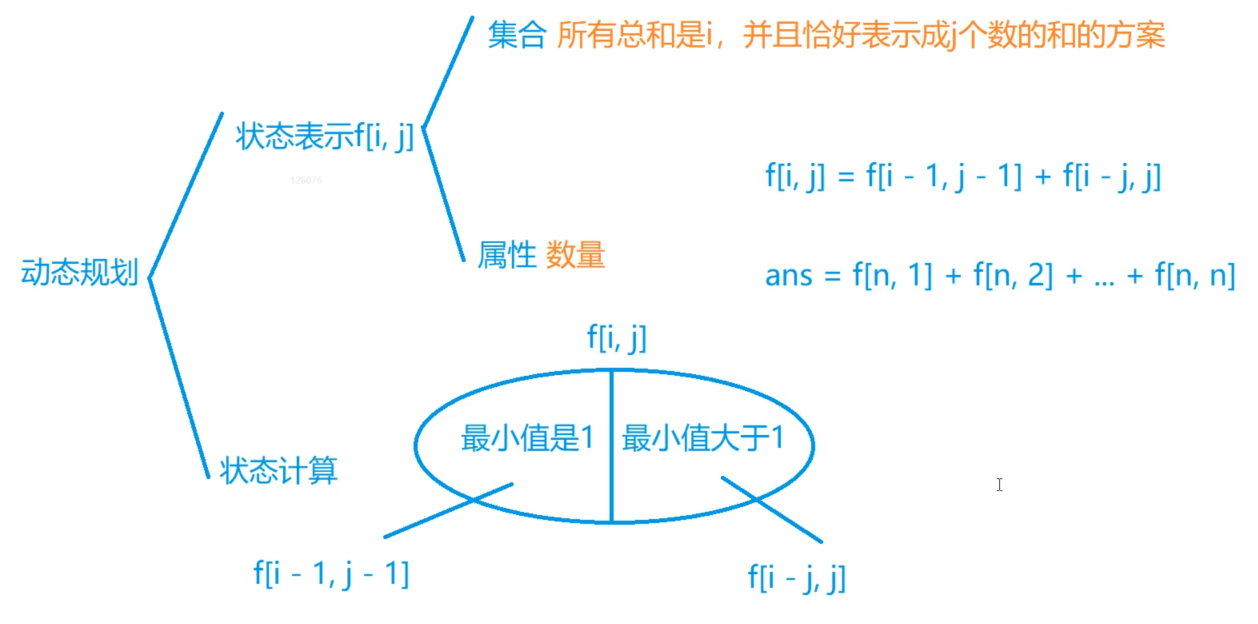 ```cpp #include <iostream> #include <algorithm> using namespace std; const int N = 1010, mod = 1e9 + 7; int n; int f[N][N]; int main() { cin >> n; f[1][1] = 1; for (int i = 2; i <= n; i ++ ) for (int j = 1; j <= i; j ++ ) f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod; int res = 0; for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod; cout << res << endl; return 0; } ``` 最后修改:2022 年 01 月 15 日 © 禁止转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏
2 条评论
好久没卷了?Σ(っ °Д °;)っ
假期是给你卷的?